
- •Модуль 1. Элементы теории чисел Глава 1.1. Целые числа §1.1.1. Теория делимости
- •Упражнения и задачи
- •§1.1.2 Наибольший общий делитель. Алгоритм Евклида
- •Упражнения и задачи
- •§1.1.3 Теорема о линейном представлении наибольшего общего делителя
- •Упражнения и задачи
- •§1.1.4 Наименьшее общее кратное
- •Упражнения и задачи
- •§1.1.5 Простые числа
- •Упражнения и задачи
- •§1.1.6 Основная теорема арифметики кольца целых чисел
- •Упражнения и задачи
- •§1.1.7 Целая часть числа
- •Упражнения и задачи
- •§1.1.8 Функция Эйлера
- •Упражнения и задачи
- •§1.1.9 Сравнения
- •Упражнения и задачи
- •§1.1.10 Полная система вычетов
- •Упражнения и задачи
- •§1.1.11 Приведенная система вычетов
- •Упражнения и задачи
- •§1.1.12 Теорема Эйлера
- •Упражнения и задачи
- •§1.1.13 Кольцо классов вычетов
- •Упражнения и задачи
- •§1.1.14 Решение сравнений
- •Упражнения и задачи
- •Контрольная работа №1 по теме “Целые числа”
- •I вариант
- •II вариант
- •III вариант
- •IV вариант
- •V вариант
- •VI вариант
- •VII вариант
- •VIII вариант
- •IX вариант
- •X вариант
- •XI вариант
- •XII вариант
- •XIII вариант
- •XIV вариант
- •XV вариант
- •XVI вариант
- •XVII вариант
- •XVIII вариант
- •XIX вариант
- •XX вариант
- •XXI вариант
- •XXII вариант
- •XXIII вариант
- •XXIV вариант
- •XXV вариант
- •XXVI вариант
- •XVII вариант
- •XXVIII вариант
- •XXIX вариант
- •XXX вариант
- •Глава 1.2. Комплексные числа и комплексные функции
- •§1.2.1 Алгебраическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.2 Комплексно сопряженные числа
- •Упражнения и задачи
- •§1.2.3 Геометрическая интерпретация комплексных чисел
- •Упражнения и задачи
- •§1.2.4 Тригонометрическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.5 Формула Муавра
- •Упражнения и задачи
- •§1.2.6 Модуль комплексного числа
- •Упражнения и задачи
- •§1.2.7 Извлечение корня из комплексного числа
- •Упражнения и задачи
- •§1.2.8 Корни из 1
- •Упражнения и задачи
- •§1.2.9 Показательная форма записи комплексного числа
- •Упражнения и задачи
Упражнения и задачи
Выписать приведенную систему вычетов наименьших неотрицательных вычетов по модулю 15.
Выписать приведенную систему наименьших по абсолютной величине вычетов по модулю 16.
Показать, что числа 13, -13, 29, -9 составляют приведенную систему вычетов по модулю 10.
Показать, что числа 11, -1, 17, -19 составляют приведенную систему вычетов по модулю 8.
§1.1.12 Теорема Эйлера
Теорема.Если![]() то
то![]()
Доказательство:Пусть числа![]() образуют приведенную систему вычетов
по модулют. Тогда числа
образуют приведенную систему вычетов
по модулют. Тогда числа![]() все взаимно просты сти попарно не
сравнимы по модулют. Число
все взаимно просты сти попарно не
сравнимы по модулют. Число![]() попадает в один класс вычетов с каким-то
попадает в один класс вычетов с каким-то![]() из чисел
из чисел![]() Число
Число![]() попадает в один класс с другим числом
попадает в один класс с другим числом![]() но из этого же множества, т.е. имеем
сравнения
но из этого же множества, т.е. имеем
сравнения
![]()
![]()
... ...
![]()
Здесь числа
![]() - те же числа
- те же числа![]() ,
записанные, может быть, в другом порядке.
Поэтому после перемножения сравнений
можно записать
,
записанные, может быть, в другом порядке.
Поэтому после перемножения сравнений
можно записать
![]()
Откуда
![]()
Что и требовалось доказать. ■
Малая теорема Ферма. Для любых целых чиселаи простого числар
![]()
Доказательство:![]() Поэтому, еслиане делится нар,
то по теореме Эйлера
Поэтому, еслиане делится нар,
то по теореме Эйлера
![]()
откуда следует, что
![]()
Если аделится нар, то![]()
![]() откуда и получим сравнение
откуда и получим сравнение![]() ■
■
Пример.Найти
остаток от деления![]() на 101.
на 101.
Решение: По малой
теореме Ферма
![]() ,
101 – простое число;
,
101 – простое число;![]() .
.
Ответ: 49.
Пример.Доказать,
что число![]() делится на 45.
делится на 45.
Решение: По теореме
Эйлера
![]() .
После возведения в пятую степень получим
.
После возведения в пятую степень получим![]() .
.
Упражнения и задачи
Проверить теорему Эйлера при
а)
![]() б)
б)![]() в)
в)![]()
Найти остатки от деления
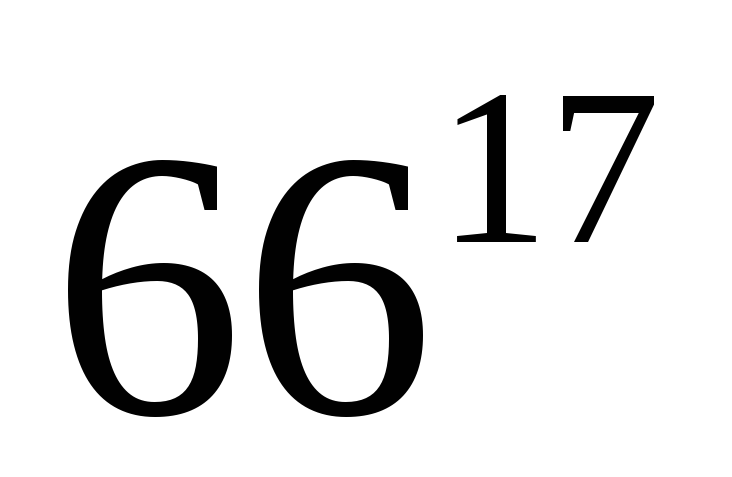 на
на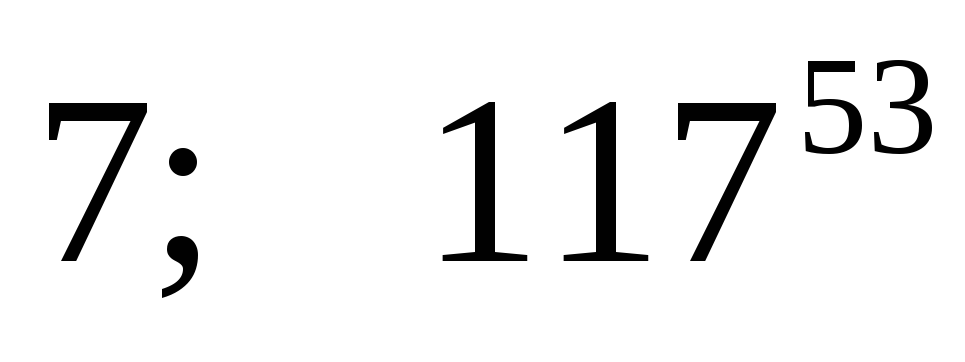 на 11.
на 11.Найти остатки от деления
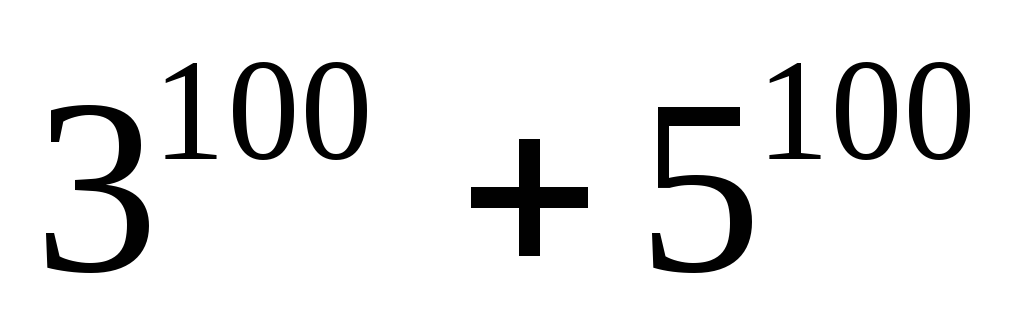 на
на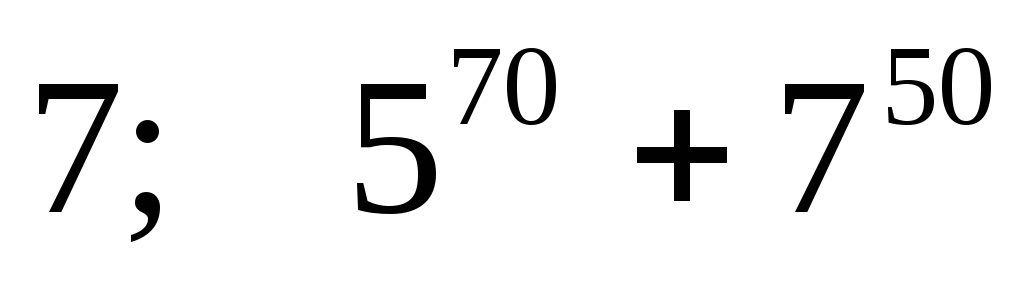 на 12.
на 12.Найти последние две цифры числа
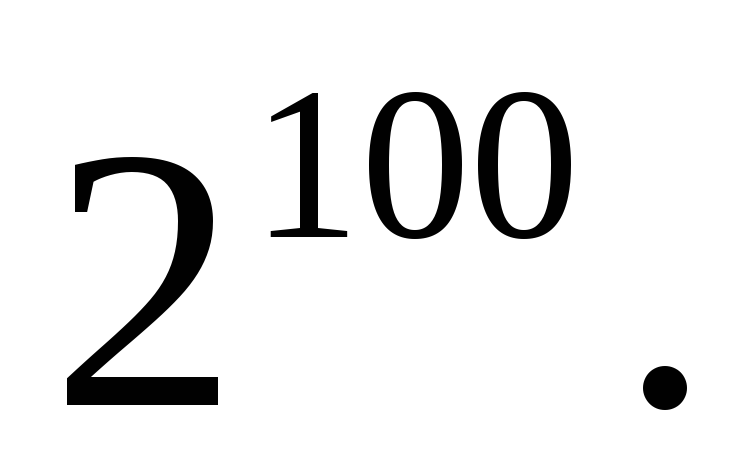
Доказать, что при любом целом п
![]()
Если
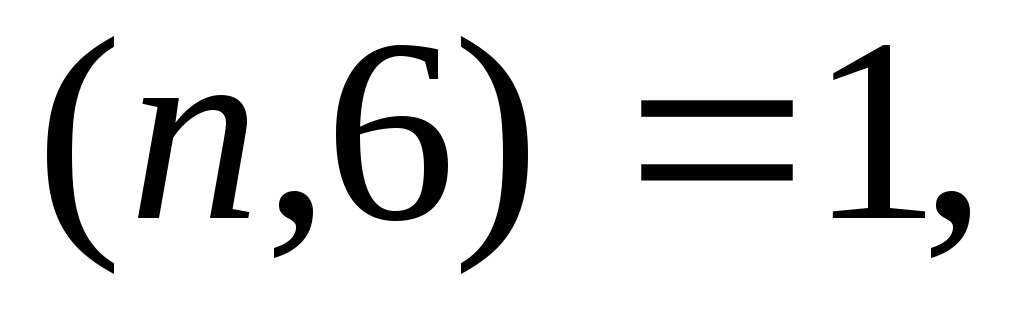 то
то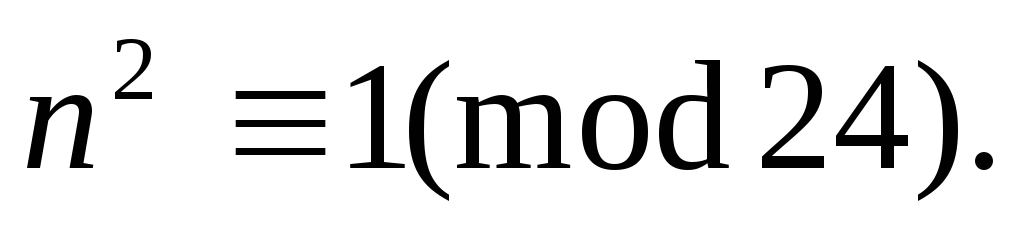
§1.1.13 Кольцо классов вычетов
Множество всех классов
вычетов по модулю тобозначается![]() или
или![]() Введем на этом множестве операции
сложения классов и умножения классов.
Введем на этом множестве операции
сложения классов и умножения классов.
Суммой классов![]() и
и![]() называется класс
называется класс![]() т.е. класс, содержащий число
т.е. класс, содержащий число![]()
Произведениемклассов![]() и
и![]() называется класс
называется класс![]() ,
т.е. класс, содержащий число
,
т.е. класс, содержащий число![]() .
.
Эти определения
корректны, так как сумма любых двух
представителей классов
![]() и
и![]() всегда попадает в один и тот же класс,
содержащий число
всегда попадает в один и тот же класс,
содержащий число![]() Аналогичное утверждение имеет место и
для произведения.
Аналогичное утверждение имеет место и
для произведения.
Действительно, если
![]() то
то![]() следовательно,
следовательно,![]() и
и![]() т.е.
т.е.![]()
Таким образом, определения суммы и произведения классов не зависят от выбора представителей классов.
Пример: Таблица сложения и умножения по модулю 6.
|
+ |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
2 |
3 |
4 |
5 |
0 |
|
2 |
2 |
3 |
4 |
5 |
0 |
1 |
|
3 |
3 |
4 |
5 |
0 |
1 |
2 |
|
4 |
4 |
5 |
0 |
1 |
2 |
3 |
|
5 |
5 |
0 |
1 |
2 |
3 |
4 |
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
2 |
0 |
2 |
4 |
0 |
2 |
4 |
|
3 |
0 |
3 |
0 |
3 |
0 |
3 |
|
4 |
0 |
4 |
2 |
0 |
4 |
2 |
|
5 |
0 |
5 |
4 |
3 |
2 |
1 |
Теорема.Относительно введенных действий сложения
и умножения классов множество![]() – ассоциативное, коммутативное кольцо
с 1.
– ассоциативное, коммутативное кольцо
с 1.
Доказательствозаключается в проверке аксиом кольца. ■
Теорема.Кольцо классов вычетов по простому модулю – поле.
Доказательство:Пустьр– простое число,![]() Тогда
Тогда![]() и по теореме Ферма
и по теореме Ферма![]() Отсюда
Отсюда![]() т.е. обратным к классу
т.е. обратным к классу![]() является класс
является класс![]() Мы получили, что любой ненулевой класс
Мы получили, что любой ненулевой класс![]() в
в![]() имеет обратный, а это означает, что
имеет обратный, а это означает, что![]() – поле. ■
– поле. ■
