
- •Модуль 1. Элементы теории чисел Глава 1.1. Целые числа §1.1.1. Теория делимости
- •Упражнения и задачи
- •§1.1.2 Наибольший общий делитель. Алгоритм Евклида
- •Упражнения и задачи
- •§1.1.3 Теорема о линейном представлении наибольшего общего делителя
- •Упражнения и задачи
- •§1.1.4 Наименьшее общее кратное
- •Упражнения и задачи
- •§1.1.5 Простые числа
- •Упражнения и задачи
- •§1.1.6 Основная теорема арифметики кольца целых чисел
- •Упражнения и задачи
- •§1.1.7 Целая часть числа
- •Упражнения и задачи
- •§1.1.8 Функция Эйлера
- •Упражнения и задачи
- •§1.1.9 Сравнения
- •Упражнения и задачи
- •§1.1.10 Полная система вычетов
- •Упражнения и задачи
- •§1.1.11 Приведенная система вычетов
- •Упражнения и задачи
- •§1.1.12 Теорема Эйлера
- •Упражнения и задачи
- •§1.1.13 Кольцо классов вычетов
- •Упражнения и задачи
- •§1.1.14 Решение сравнений
- •Упражнения и задачи
- •Контрольная работа №1 по теме “Целые числа”
- •I вариант
- •II вариант
- •III вариант
- •IV вариант
- •V вариант
- •VI вариант
- •VII вариант
- •VIII вариант
- •IX вариант
- •X вариант
- •XI вариант
- •XII вариант
- •XIII вариант
- •XIV вариант
- •XV вариант
- •XVI вариант
- •XVII вариант
- •XVIII вариант
- •XIX вариант
- •XX вариант
- •XXI вариант
- •XXII вариант
- •XXIII вариант
- •XXIV вариант
- •XXV вариант
- •XXVI вариант
- •XVII вариант
- •XXVIII вариант
- •XXIX вариант
- •XXX вариант
- •Глава 1.2. Комплексные числа и комплексные функции
- •§1.2.1 Алгебраическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.2 Комплексно сопряженные числа
- •Упражнения и задачи
- •§1.2.3 Геометрическая интерпретация комплексных чисел
- •Упражнения и задачи
- •§1.2.4 Тригонометрическая форма комплексного числа
- •Упражнения и задачи
- •§1.2.5 Формула Муавра
- •Упражнения и задачи
- •§1.2.6 Модуль комплексного числа
- •Упражнения и задачи
- •§1.2.7 Извлечение корня из комплексного числа
- •Упражнения и задачи
- •§1.2.8 Корни из 1
- •Упражнения и задачи
- •§1.2.9 Показательная форма записи комплексного числа
- •Упражнения и задачи
Упражнения и задачи
Вычислить:
а)
![]() б)
б)![]() в)
в)![]() г)
г)![]() д)
д)![]()
Представить в алгебраической форме:
а)
![]() б)
б)![]() в)
в)![]()
Выполнить действия:
а)
![]() б)
б)![]() в)
в)![]()
Представить в алгебраической форме:
а)
![]() б)
б)![]() в)
в)![]()
Решить уравнения:
а)
![]() б)
б)![]() в)
в)![]()
Решить систему
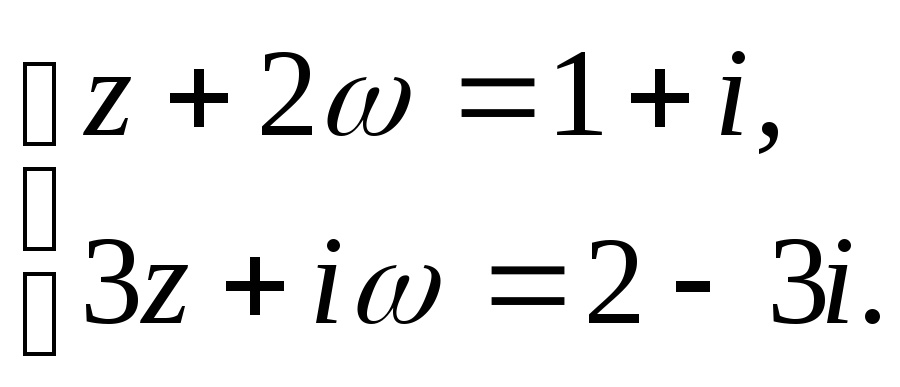
§1.2.2 Комплексно сопряженные числа
Для
![]() комплексное число
комплексное число![]() называетсясопряженным. Имеют место
равенства:
называетсясопряженным. Имеют место
равенства:
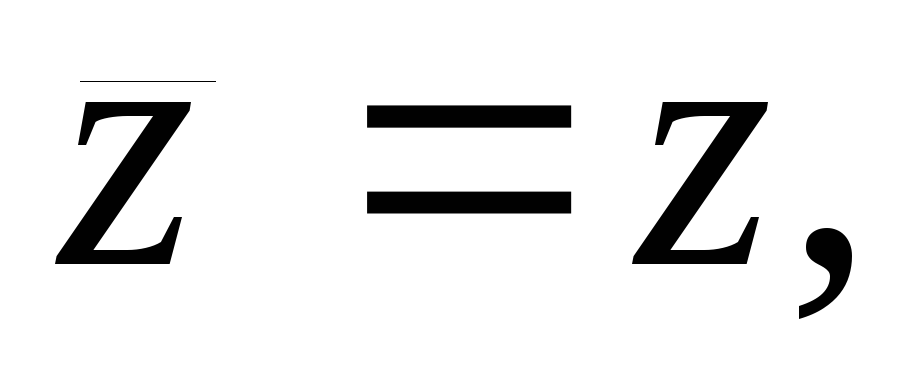 т.е.zи
т.е.zи сопряжены друг другу;
сопряжены друг другу;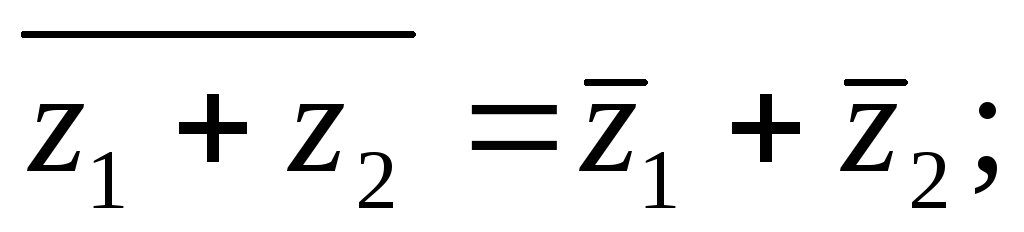
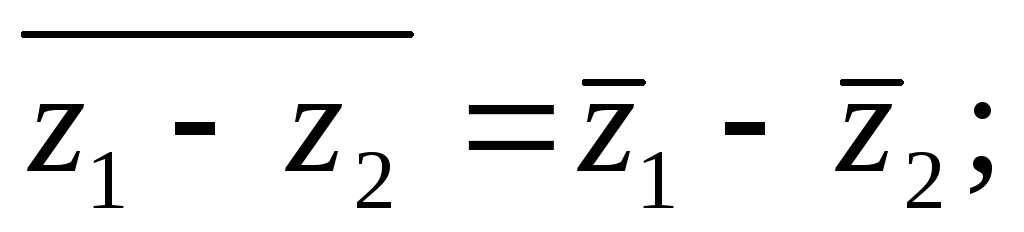
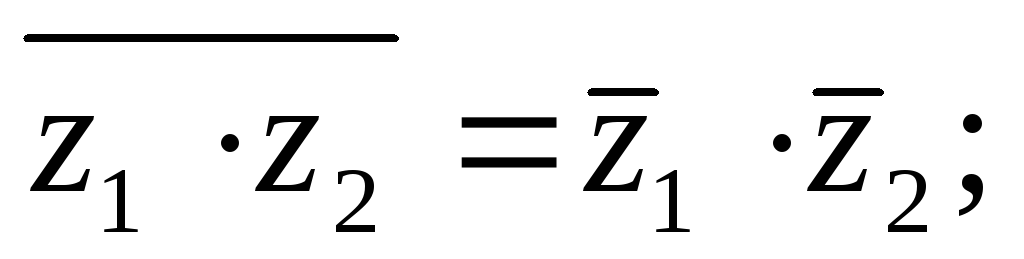
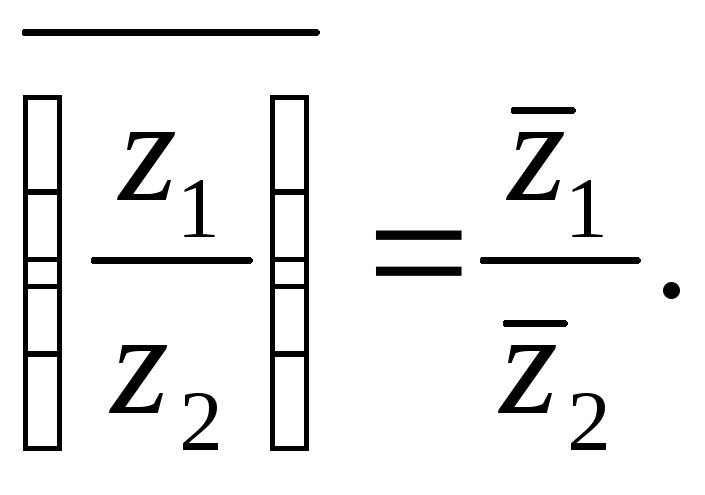
Отсюда непосредственно вытекает.
Теорема.Пусть имеется выражение, составленное из комплексных чисел, над которыми совершается ряд рациональных операций (сложение, умножение, вычитание, деление, возведение в целую степень). Если каждое из этих чисел заменить на сопряженное, то и значение всего выражения заменится на сопряженное. ■
Заметим, что произведение
и сумма сопряженных чисел являются
действительными числами:
![]() Ясно
также, что
Ясно
также, что![]()
Пример.Найти число
сопряженное числу![]()
Решение:
![]()
Пример.Доказать
тождество![]()
Доказательство:Пусть![]() Тогда
Тогда![]()
![]()
Аналогично получим,
что
![]() Поэтому:
Поэтому:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Упражнения и задачи
Представить в алгебраической форме
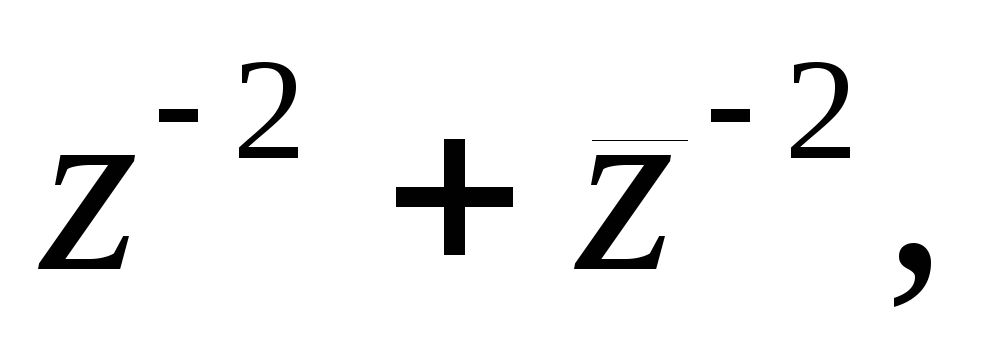 если
если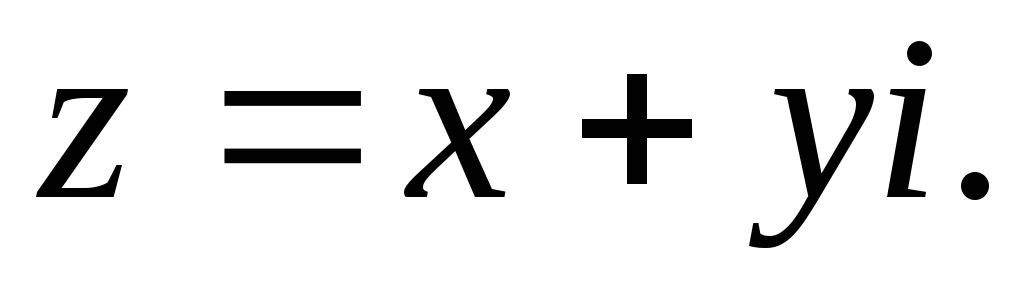
Решить уравнение:
а)
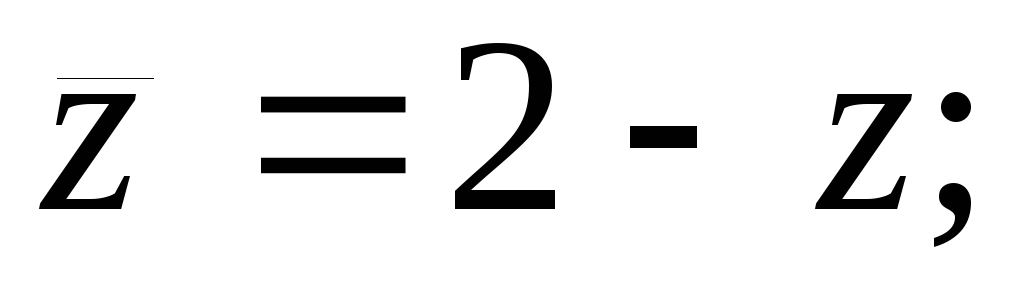 б)
б)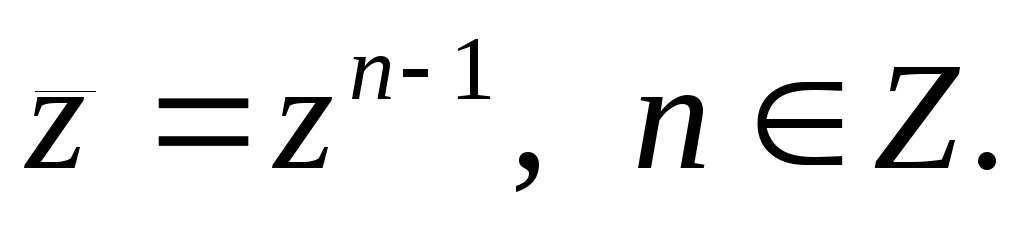
Если с– корень многочлена с действительными коэффициентами, то и число
 ,
сопряженное числус, также корень
этого многочлена. Доказать это.
,
сопряженное числус, также корень
этого многочлена. Доказать это.Показать, что числа
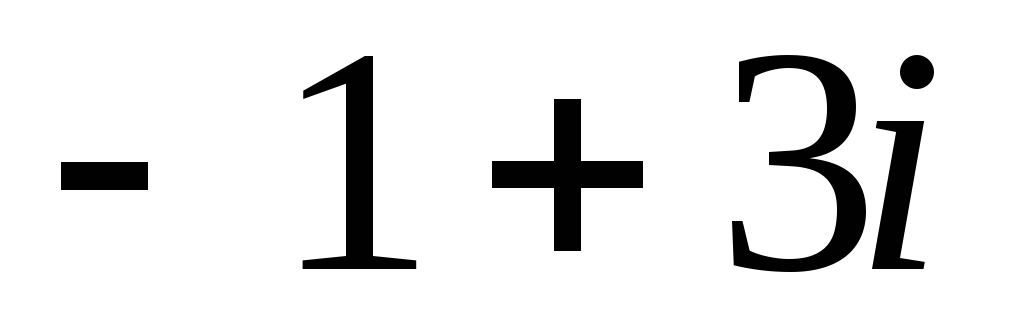 и
и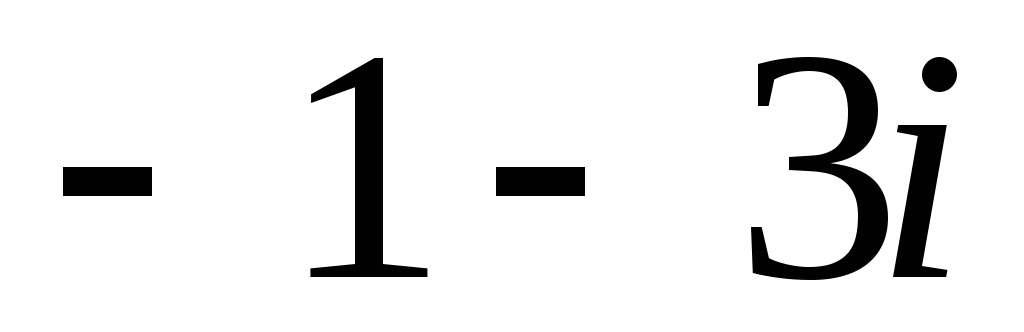 удовлетворяют уравнению
удовлетворяют уравнению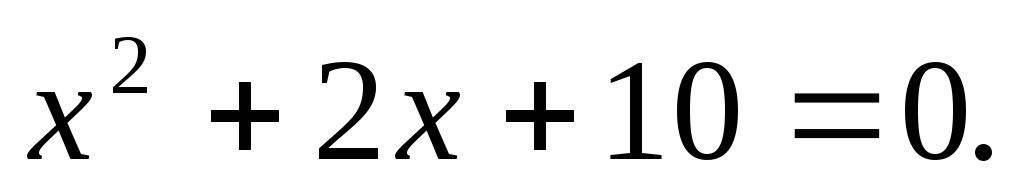
Если
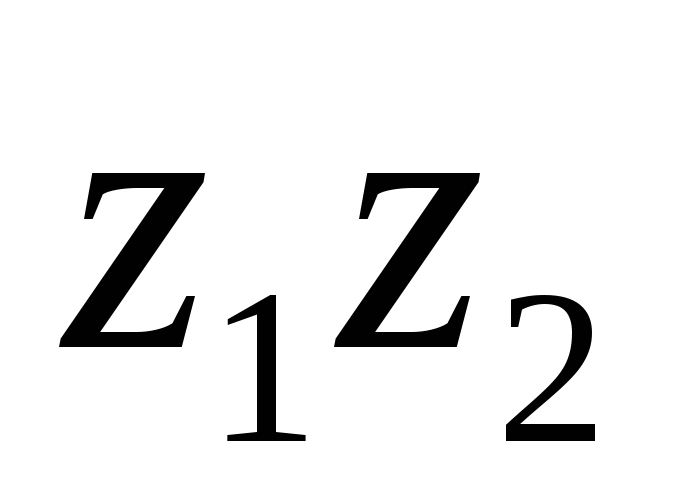 – действительное число, то
– действительное число, то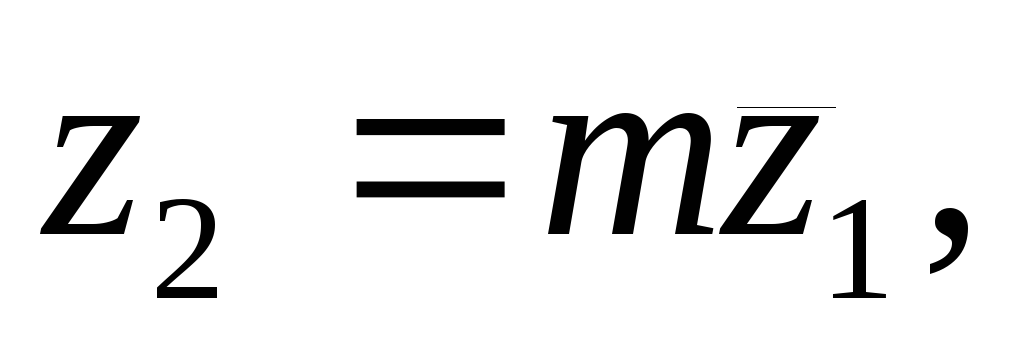 где
где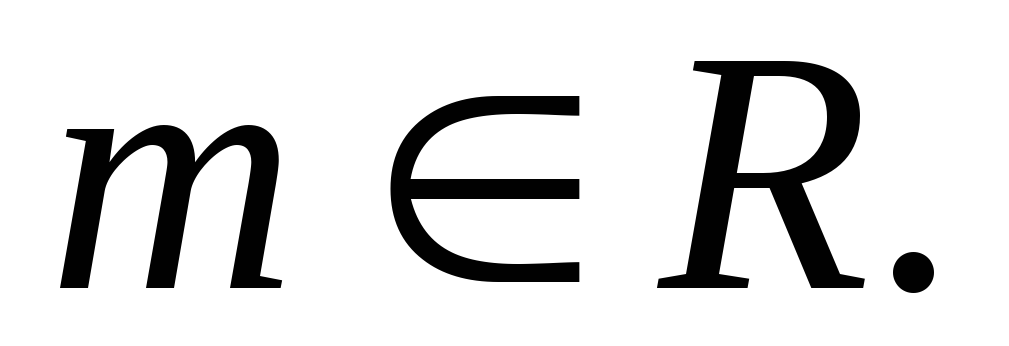 Доказать это.
Доказать это.
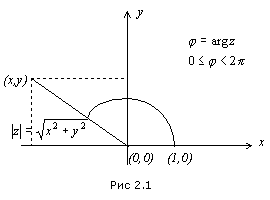
§1.2.3 Геометрическая интерпретация комплексных чисел
Поставим каждому числу
![]() в соответствие точку с координатами
в соответствие точку с координатами![]() в прямоугольной декартовой системе
координатXOY, т.е.
установим взаимно однозначное соответствие
между множеством комплексных чисел и
точками плоскостиXOY(см. рис. 2.1). ПлоскостьXOY,
служащая для изображения комплексных
чисел, называетсяплоскостью комплексной
переменной.ОсьOXназывается действительной осью; на ней
изображаются действительные числа. ОсьOY-мнимаяось; на
ней изображаются чистомнимые числа.
в прямоугольной декартовой системе
координатXOY, т.е.
установим взаимно однозначное соответствие
между множеством комплексных чисел и
точками плоскостиXOY(см. рис. 2.1). ПлоскостьXOY,
служащая для изображения комплексных
чисел, называетсяплоскостью комплексной
переменной.ОсьOXназывается действительной осью; на ней
изображаются действительные числа. ОсьOY-мнимаяось; на
ней изображаются чистомнимые числа.
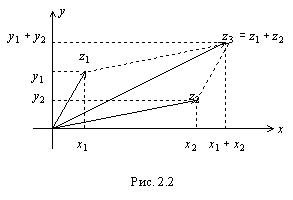
Сложение и вычитание
комплексных чисел получают простое
геометрическое истолкование. Для всякого
комплексного числа
![]() вектор
вектор![]() имеет своими проекциями на осиOX,
OYсоответственно
числаx, y.Пусть теперь
имеет своими проекциями на осиOX,
OYсоответственно
числаx, y.Пусть теперь![]() Тогда для
Тогда для![]() имеем
имеем
![]()
О

 тсюда
вытекает, что проекциями вектора
тсюда
вытекает, что проекциями вектора![]() на
оси координат оказываются суммы
соответствующих проекций векторов
на
оси координат оказываются суммы
соответствующих проекций векторов![]() и
и![]() ;
иными словами сумма находится по правилу
параллелограмма сложения векторов
;
иными словами сумма находится по правилу
параллелограмма сложения векторов
![]() .
.
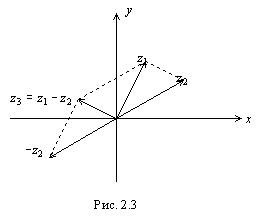
Если
![]() то
то![]() и для построения вектора
и для построения вектора![]() в этом случае мы должны сложить векторы
в этом случае мы должны сложить векторы![]() и -
и -![]() (см. рис. 2.3), т.е. получим вектор, равный
вектору
(см. рис. 2.3), т.е. получим вектор, равный
вектору![]() (вторая диагональ того же параллелограмма).
(вторая диагональ того же параллелограмма).
Расстояние от точки
![]() до начала координат равно
до начала координат равно![]() Величина
Величина![]() называетсямодулемкомплексного
числа
называетсямодулемкомплексного
числа![]() .
Для действительного числа он совпадает
с понятием абсолютной величины. Модуль
комплексного числа неотрицателен и
определен однозначно;
.
Для действительного числа он совпадает
с понятием абсолютной величины. Модуль
комплексного числа неотрицателен и
определен однозначно;![]() Угол
Угол![]() отсчитываемый против часовой стрелки
от луча
отсчитываемый против часовой стрелки
от луча![]() до луча
до луча![]() называетсяглавным аргументом числа
называетсяглавным аргументом числа![]() и обозначается
и обозначается![]() Величина
Величина![]() может быть найдена из системы:
может быть найдена из системы:
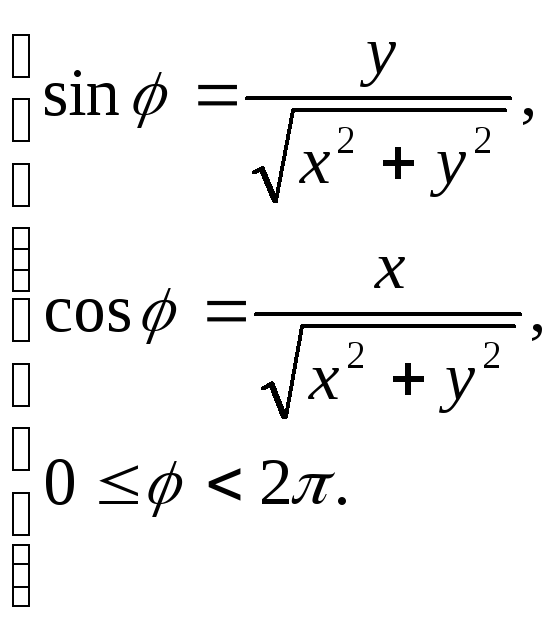
Аргументомкомплексного числаz
(Argz)
называется любое из чисел вида![]() где
где![]() т.е. аргумент определен с точностью до
т.е. аргумент определен с точностью до![]() Для числаz= 0 аргументом
может быть любое число.
Для числаz= 0 аргументом
может быть любое число.
Пример.Изобразить на плоскости число 1+i, найти его модуль и аргумент.
Решение:
![]() т.е.
т.е.![]() т.е.
т.е.![]()
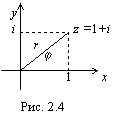
Пример.Изобразить
на плоскости множество всех точек, для
которых![]()
Решение:![]() Следовательно
Следовательно
![]() или
или![]()
Получили уравнение окружности радиуса 2 с центром в точке (-2; 0).
Пример.Изобразить
на плоскости множество всех точек, для
которых
![]()
Ответ:Луч с началом
в точке (0; 0) и проходящий под углом![]() к осиOX.
к осиOX.
Теория комплексных чисел может быть использована при решении планиметрических задач.
Пример.Доказать,
что![]()
Доказательство:Поскольку
![]() то
то![]()
![]()
![]() Тем самым доказано, что сумма квадратов
диагоналей параллелограмма равна сумме
квадратов всех его сторон.
Тем самым доказано, что сумма квадратов
диагоналей параллелограмма равна сумме
квадратов всех его сторон.
