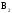- •Федеральное агентство по образованию
- •Содержание
- •Рабочая программа
- •Краткие теоретические сведения
- •Примеры составления математических моделей
- •2. Зпр в условиях определенности
- •3. Принятие решения в условиях неопределенности
- •4. Принятие решения в условиях риска
- •5. Элементы теории игр
- •Контрольные задания
- •Основная литература
- •Дополнительная литература
5. Элементы теории игр
В практической деятельности весьма часто приходится рассматривать явления и ситуации, в которых участвуют две или более стороны, имеющие различные интересы и обладающие возможностями применения для достижения своих целей разнообразные действия. Подобные явления и ситуации принято называть конфликтными, или просто конфликтами.
Типичный конфликт характеризуется тремя основными составляющими:
Заинтересованными сторонами.
Возможными действиями этих сторон.
Интересами сторон.
Необходимость изучения и анализа конфликтов, представляемых в виде упрощенных математических моделей (игр), вызвала к жизни специальный математический аппарат – теорию игр.
Опишем некоторые основные понятия, используемые в этой теории.
Заинтересованные стороны называются игроками. Любое возможное для игрока действие (в рамки заданных правил игры) называется его стратегией. В условиях конфликта каждый игрок выбирает свою стратегию, в результате чего складывается набор стратегий, называемый ситуацией. Заинтересованность игроков в ситуации проявляется в том, что каждому игроку в каждой ситуации приписывается число, выражающее степень удовлетворения его интересов в этой ситуации и называемое его выигрышем в ней.
Изучение игр можно проводить с различных точек зрения. Мы будем стремиться к
- выработке принципов оптимальности, то есть того, какое поведение игроков следует считать оптимальным (разумным, целесообразным);
- выяснению реализуемости этих принципов, то есть установлению существования оптимальных в выработанном смысле ситуаций;
- отысканию этих реализаций.
Одной из плодотворных форм реализации представлений об оптимальности можно считать понятие равновесия, при котором складывается такая (равновесная) ситуация, в нарушении которой не заинтересован ни один из игроков.
Если в игре ситуации равновесия (в пределах отпущенных возможностей) нет, то, оставаясь в условиях стратегий, имеющихся у игроков, мы сталкиваемся с неразрешимой задачей. При возникновении подобных случаев естественно ставить вопрос о таком расширении первоначального понятия стратегии, чтобы среди ситуаций, составленных из новых, обобщенных стратегий, заведомо нашлись бы равновесные. Если такие обобщенные стратегии существуют, то обычно они представляются некоторыми комбинациями исходных стратегий (при этом, естественно, предполагается, что игра повторяется многократно). Для того чтобы отличить первые стратегии от новых, первые называют чистыми, а вторые – смешанными стратегиями.
Весьма плодотворным является представление смешанной стратегии как случайного выбора игроками их чистых стратегий, при котором случайные выборы различных игроков независимы в совокупности, а выигрыш каждого из них определяется как математическое ожидание случайного выигрыша. Игра, преобразованная таким образом, обычно называется смешанным расширением исходной игры.
Матричная игра
Проиллюстрируем сказанное на примере одного из самых простых, но одновременно и наиболее изученных классов игр, на так называемых матричных играх. Исследование матричных игр интересно еще и потому, что к ним могут быть приближенно сведены многие игры более общего вида.
Рассмотрим следующий пример.
Пример . Два игрока А и В, не глядя друг на друга, кладут на стол по картонному кружку красного, зеленого или синего цветов, и расплачиваются друг с другом так, как показано в матрице игры

(напомним,
что у этой 3 3-матрицы
строки соответствуют стратегиям игрока
А, а столбцы – стратегиям игрока В).
3-матрицы
строки соответствуют стратегиям игрока
А, а столбцы – стратегиям игрока В).
Считая,
что эта 3 3
игра повторяется многократно, попробуем
определить оптимальные стратегии
каждого из игроков.
3
игра повторяется многократно, попробуем
определить оптимальные стратегии
каждого из игроков.
Начнем с последовательного анализа стратегий игрока А, не забывая о том, что выбирая стратегию игрока А, должно принимать в расчет, что его противник В может ответить на нее той из своих стратегий, при которой выигрыш игрока А будет минимальным.
Запишем эти минимальные выигрыши в правом столбце таблицы:
|
|
|
|
|
|
|
A1 |
-2 |
2 |
-1 |
-2 |
|
A2 |
2 |
1 |
1 |
1 |
|
A3 |
3 |
-3 |
1 |
-3 |

Если игрок А будет придерживаться этой стратегии, то ему гарантирован выигрыш, не меньший 1, при любом поведении противника в игре.
Аналогичные рассуждения можно провести и за игрока В. Так как игрок В заинтересован в том, чтобы обратить выигрыш игрока А в минимум, то ему нужно проанализировать каждую свою стратегию с точки зрения максимального выигрыша игрока А.
|
|
B1 |
B2 |
B3 |
|
|
A1 |
-2 |
2 |
-1 |
-2 |
|
A2 |
2 |
1 |
1 |
1 |
|
A3 |
3 |
-3 |
1 |
-3 |
|
|
3 |
2 |
1 |
|

Если игрок В будет придерживаться этой стратегии, то при любом поведении противника он проиграет не больше 1.
В рассматриваемой игре числа maxmin и minmax совпали:
 =
=
 =1.
=1.
Выделенные стратегии A2 и B3 являются стратегиями игроков А и В,
в следующем смысле:
при многократном повторении игры отказ от выбранной стратегии любым из игроков уменьшает его шансы на выигрыш (увеличивает шансы на проигрыш).
Тем
самым, ситуация
 оказывается равновесной.
оказывается равновесной.
Число
 называетсянижней
ценой игры.
называетсянижней
ценой игры.
Число
 называетсяверхней
ценой игры.
называетсяверхней
ценой игры.
Если
 ,то
ситуация
,то
ситуация оказывается равновесной, и ни один из
игроков не заинтересован в том, чтобы
ее нарушить (в этом нетрудно убедиться
путем рассуждений, подобных проведенным
при анализе игры).
оказывается равновесной, и ни один из
игроков не заинтересован в том, чтобы
ее нарушить (в этом нетрудно убедиться
путем рассуждений, подобных проведенным
при анализе игры).
В
том случае, когда нижняя цена игры равна
верхней цене игры, их общее значение
называется просто ценой
игры и
обозначается через
 .
.
Цена
игры совпадает с элементом
 матрицы игры А, расположенным на
пересечении
матрицы игры А, расположенным на
пересечении -й
строки и
-й
строки и -го
столбца – минимальным в своей строке
и максимальным в своем столбце.
-го
столбца – минимальным в своей строке
и максимальным в своем столбце.
Этот элемент называют седловой точкой матрицы А, или точкой равновесия, а про игру говорят, что она имеет седловую точку.
Стратегии
 и
и ,
соответствующие седловой точке,
называютсяоптимальными,
а
совокупность оптимальных ситуаций и
цена игры – решением
матричной игры с седлововй точкой.
,
соответствующие седловой точке,
называютсяоптимальными,
а
совокупность оптимальных ситуаций и
цена игры – решением
матричной игры с седлововй точкой.
Замечание. Седловых точек в матричной игре может быть несколько, но все они имеют одно и то же значение.
Матричные игры с седловой точкой важны и интересны, однако более типичным является случай, когда применение описанного алгоритма приводит к неравенству
 .
.
Применение
минимаксных стратегий для каждого из
игроков обеспечивает выигрыш, не
превышающий
 ,
и проигрыш, не меньший β. Для каждого
игрока естественен вопрос увеличения
выигрыша ( уменьшения проигрыша). Поиски
такого решения состоят в том, что игроки
1) применяют не одну, а несколько стратегий,
выбор которых осуществляется случайным
образом; 2) “ смешивают ” свои стратегии,
чередуя их случайным образом с какими-то
вероятностями.
,
и проигрыш, не меньший β. Для каждого
игрока естественен вопрос увеличения
выигрыша ( уменьшения проигрыша). Поиски
такого решения состоят в том, что игроки
1) применяют не одну, а несколько стратегий,
выбор которых осуществляется случайным
образом; 2) “ смешивают ” свои стратегии,
чередуя их случайным образом с какими-то
вероятностями.
Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, как поведет себя противник в данной партии.
Обозначим смешанные стратегии игроков А и В через Р = { p1, р2, …,рm} и Q = { q1, q2,…, qn} соответственно, где p1, р2, …,рm(образующие в сумме единицу) – вероятности применения игроком А стратегий А1, А2, …, Аm; q1, q2,…, qn – вероятности применения игроком В стратегий В1, В2, …, Вn.
Существует так называемая основная теорема теории игр: любая конечная игра двух лиц с нулевой суммой имеет по крайней мере одно решение, возможно, в области смешанных стратегий.
Применение оптимальной смешанной стратегии позволяет получить выигрыш, равный цене игры:
α
 υ
υ β.
β.
Рассмотрим пример наиболее простой матричной игры, в которой один из игроков имеет две стратегии. Решение такой игры можно найти графически.
Пример.
Найдите
решение следующей матричной игры
 .
.
Решение:
|
|
|
|
min |
|
|
1 |
4 |
1 |
|
|
3 |
-2 |
-2 |
|
|
0 |
5 |
0 |
|
mах: |
3 |
5 |
0 |
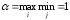 -
нижняя цена игры
-
нижняя цена игры -
верхняя цена игры
-
верхняя цена игры
Т.к.
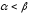 ,
то имеет место матричная игра в смешанных
стратегиях,седловой
точки нет.
,
то имеет место матричная игра в смешанных
стратегиях,седловой
точки нет.
Пусть
 - произвольная смешанная стратегия
игрока В. Если игрок А выбирает
- произвольная смешанная стратегия
игрока В. Если игрок А выбирает чистую стратегию, то средний выигрыш
игрока В ситуации
чистую стратегию, то средний выигрыш
игрока В ситуации будет равным
будет равным ,
где
,
где .
Зависимость этого выигрыша от переменной
.
Зависимость этого выигрыша от переменной описывается прямой.
описывается прямой.
|
|
|
|
1 |
4 |
|
3 |
-2 |
|
0 |
5 |
(1)
(2)

(3)


Выделим верхнюю огибающую. Нижняя точка верхней огибающей является точкой пересечения прямых (1) и (2). Получим,

 ,
значитQ
= {
,
значитQ
= {
 }
}
Полагая
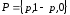 ,
получим:
,
получим:
|
р |
1 |
4 |
|
1-р |
3 |
-2 |
|
0 |
0 |
5 |

 ,
значит Р = {
,
значит Р = {
 ,
,
 }
}
Цена
игры υ = ω0
=

Ответ:
Р = {
 ,
,
 };Q
= {
};Q
= {
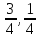 };υ
=
};υ
=
 .
.
Биматричная игра
Часто встречаются ситуации, в которых интересы игроков хотя и не совпадают, но уже не обязательно являются противоположными.
Рассмотрим конфликтную ситуацию, в которой каждый из двух участников имеет следующие возможности для выбора своей линии поведения:
игрок А – может выбрать любую из стратегий А1, А2,…, Аm,
игрок В – любую из стратегий В1, В2,…, Вn.
При этом всякий раз их совместный выбор оценивается вполне определенно:
если
игрок А выбрал i-ю
стратегию, а игрок В – k-ю
стратегию, то в игре выигрыш игрока А
будет равен некоторому числу
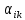 ,
а выигрыш игрока В некоторому другому
числу
,
а выигрыш игрока В некоторому другому
числу
 .
.
Иными словами, всякий раз каждый из игроков получает свой приз.
Последовательно перебирая стратегии обоих игроков можно заполнить их матрицы выигрышей. Таким образом, получим две платежные матрицы, отсюда и называние - биматричная игра.
Пример. Фирма А намерена сбыть партию товара на одном из двух рынков, которые контролируются более крупной фирмой В. С этой целью она проводит подготовительную работу, связанную с определенными затратами. Если фирма В разгадает, на каком рынке фирма А будет продавать свой товар, то она примет контрмеры и воспрепятствует “захвату” рынка (этот вариант означает поражение фирмы А); если нет, то фирма А одерживает победу. Предположим, что для фирмы А проникновение на первый рынок более выгодно, чем проникновение на второй, но и борьба за первый рынок требует от нее больших средств. Например, победа фирмы А на первом рынке приносит ей вдвое большую прибыль, чем победа на втором, но зато поражение на первом рынке полностью ее разоряет. Пусть для фирмы А ее победа на первом рынке оценивается в 2 ед., а на втором рынке – в 1 ед.; поражение фирмы А на первом рынке оценивается в 10 ед., а на втором – в -1 ед. Для фирмы В ее победа составляет соответственно 5 и 1 ед., а поражение -2 и -1 ед.
В результате получаем биматричную игру с матрицами выигрышей


Решение. Существуют специальные методы решения биматричных игр, но мы воспользуемся способом решения матричной игры, разбив данную игру на две матричные.
Игра с матрицей

Решая
эту игру графическим методом, найдем
оптимальную смешанную стратегию для
игрока А (фирмы А) - { },
},
цену
этой игры
 =
–
=
– ,
,
а
затем и оптимальную смешанную стратегию
для игрока В - { }.
}.
Игра с матрицей

Решая
эту игру графическим методом, найдем
оптимальную смешанную стратегию для
игрока В (фирмы В) - { },
},
цену
этой игры
 =
= ,
,
а
затем и оптимальную смешанную стратегию
для игрока А - {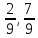 }.
}.
Таким
образом, соответствующие смешанные
стратегии игроков имеют следующий вид
Р = { },Q
= {
},Q
= { },
},
а средние выигрыши игроков таковы
HA
= -
 ,HВ
=
,HВ
=
 .
.
Замечание.
Первые элементы полученных множеств
являются координатами точки равновесия,
в нашем случае это будет точка ( )
)
Ответ:
Р ={
 },Q
= {
},Q
= { },HA
= -
},HA
= -
 ,HВ
=
,HВ
=
 .
.