
- •Федеральное агентство по образованию
- •Содержание
- •Рабочая программа
- •Краткие теоретические сведения
- •Примеры составления математических моделей
- •2. Зпр в условиях определенности
- •3. Принятие решения в условиях неопределенности
- •4. Принятие решения в условиях риска
- •5. Элементы теории игр
- •Контрольные задания
- •Основная литература
- •Дополнительная литература
2. Зпр в условиях определенности
При принятии решения в условиях определенности состояние среды является фиксированным и оно известно принимающему решение. В этом случае исход однозначно определяется выбором альтернативы, поэтому выбор альтернативы здесь эквивалентен выбору исхода.
Итак,
построение математической модели
сводится к указанию множества допустимых
альтернатив X
и заданию целевой функции f
: Х
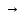 R.
В этом случае оптимальной считается та
допустимая альтернатива x*
R.
В этом случае оптимальной считается та
допустимая альтернатива x* X,
которая является не менее предпочтительной,
чем любая другая допустимая альтернатива
x
X,
которая является не менее предпочтительной,
чем любая другая допустимая альтернатива
x X;
в терминах целевой функции это означает,
что оптимальная
альтернатива должна доставлять максимум
целевой функции.
X;
в терминах целевой функции это означает,
что оптимальная
альтернатива должна доставлять максимум
целевой функции.
Замечание. Если целевая функция рассматривается как функция потерь, то оптимальной будет та допустимая альтернатива, которая доставляет минимум функции потерь.
Алгоритм
нахождения максимального (минимального)
значения функции одной переменной
изложен в курсе математического анализа
и уже знаком студентам на этапе изучения
дисциплины “Теория
принятия решений”,
поэтому остановимся на вопросе решения
ЗПР, задаваемых целевыми функциями вида
f:
D
→ R,
где D
 Rn,
n
Rn,
n ,
D
– область допустимых решений.
,
D
– область допустимых решений.
Вопрос связанный с нахождением точек экстремума для функции n переменных технически является более сложным, чем для функции одной переменной. Достаточные условия существования экстремума функции n переменных дает следующая теорема.
Теорема
Вейерштрасса.
Непрерывная функция f,
заданная в замкнутой ограниченной
области D
 Rn,
достигает в этой области как глобального
максимума, так и глобального минимума.
Rn,
достигает в этой области как глобального
максимума, так и глобального минимума.
Для
случая функции двух переменных задача
нахождения ее экстремума в области D
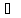 Rn
(задача линейного программирования)
легко может быть решена графическим
методом.
Rn
(задача линейного программирования)
легко может быть решена графическим
методом.
Графический метод решения
Графический метод используется для решения задач с двумя переменными следующего вида:



Данный метод основывается на возможности графического изображения области допустимых решений задачи и нахождения среди них оптимального решения.
Область
допустимых решений задачи строится как
пересечение (общая часть) областей
решений каждого из заданных ограничений.
Областью решений линейного неравенства
 является одна из двух полуплоскостей,
на которые прямая
является одна из двух полуплоскостей,
на которые прямая![]() ,
соответствующая данному неравенству,
делит всю координатную плоскость. Для
того, чтобы определить, какая из двух
координатных полуплоскостей является
областью решений, достаточно координаты
какой-либо точки, не лежащей на прямой,
подставить в неравенство: если оно
удовлетворяется, то областью решений
является полуплоскость, содержащая
данную точку, если же неравенство не
удовлетворяется, то областью решений
является полуплоскость, не содержащая
данную точку. Областью допустимых
решений задачи является общая часть
полуплоскостей – областей решений всех
неравенств системы ограничений.
,
соответствующая данному неравенству,
делит всю координатную плоскость. Для
того, чтобы определить, какая из двух
координатных полуплоскостей является
областью решений, достаточно координаты
какой-либо точки, не лежащей на прямой,
подставить в неравенство: если оно
удовлетворяется, то областью решений
является полуплоскость, содержащая
данную точку, если же неравенство не
удовлетворяется, то областью решений
является полуплоскость, не содержащая
данную точку. Областью допустимых
решений задачи является общая часть
полуплоскостей – областей решений всех
неравенств системы ограничений.
Для нахождения среди допустимых решений оптимального решения используют линии уровня и опорные прямые.
Линией
уровня называется прямая, на которой
целевая функция задачи принимает
постоянное значение. Уравнение линии
уровня в общем случае имеет вид
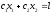 ,
где
,
где .
Все линии уровня параллельны между
собой. Их нормаль
.
Все линии уровня параллельны между
собой. Их нормаль![]() .
.
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находится оптимальное решение.
Значения целевой функции на линиях уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.
Алгоритм графического метода решения задачи линейного программирования:
1. Построить область допустимых решений.
2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений.
3. Если
область допустимых решений является
непустым множеством, построить нормаль
линий уровня
![]() и одну из линий уровня, имеющую общие
точки с этой областью.
и одну из линий уровня, имеющую общие
точки с этой областью.
4. Линию уровня переместить до опорной прямой в задаче на максимум в направлении нормали, в задаче на минимум – в противоположном направлении.
5. Если при перемещении линии уровня по области допустимых решений в направлении, соответствующем приближению к экстремуму целевой функции, линии уровня уходят в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
6. Если задача линейного программирования имеет оптимальное решение, то для его нахождения решить совместно уравнения прямых, ограничивающих область допустимых решений и имеющих общие точки с соответствующей опорной прямой. Если целевая функция задачи достигает экстремума в двух угловых точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих точек. После нахождения оптимального решения вычислить значение целевой функции в этой точке.
Пример. Решить задачу линейного программирования




Решение.Строим область допустимых
решений задачи. Нумеруем ограничения
задачи. В прямоугольной декартовой
системе координат (см. рис. на стр.
10) строим прямую 2![]() ,
соответствующую ограничению (1). Находим,
какая из двух полуплоскостей, на которые
эта прямая делит всю координатную
плоскость, является областью решений
неравенства (1). Для этого достаточно
координаты какой-либо точки, не лежащей
на прямой, подставить в неравенство.
Так как данная прямая не проходит через
начало координат, подставляем координаты
точкиО(0,0) в первое ограничение
,
соответствующую ограничению (1). Находим,
какая из двух полуплоскостей, на которые
эта прямая делит всю координатную
плоскость, является областью решений
неравенства (1). Для этого достаточно
координаты какой-либо точки, не лежащей
на прямой, подставить в неравенство.
Так как данная прямая не проходит через
начало координат, подставляем координаты
точкиО(0,0) в первое ограничение .
Получим неравенство
.
Получим неравенство .
Следовательно, точкаОне лежит в
полуплоскости решений. Таким образом,
стрелки на концах данной прямой должны
быть направлены в полуплоскость, не
содержащую точкуО. Аналогично
строим прямые
.
Следовательно, точкаОне лежит в
полуплоскости решений. Таким образом,
стрелки на концах данной прямой должны
быть направлены в полуплоскость, не
содержащую точкуО. Аналогично
строим прямые![]() ,
,![]() и области решений ограничений (2) и (3).
Находим общую часть полуплоскостей,
учитывая при этом условие неотрицательности
переменных. Полученную область допустимых
решений отметим на рис. штриховкой.
и области решений ограничений (2) и (3).
Находим общую часть полуплоскостей,
учитывая при этом условие неотрицательности
переменных. Полученную область допустимых
решений отметим на рис. штриховкой.
Строим нормаль линий уровня
 и одну из этих линий, например
и одну из этих линий, например .
Так как решается задача на отыскание
максимума целевой функции, то линию
уровня перемещаем в направлении нормали
до опорной прямой. Эта прямая проходит
через точку
.
Так как решается задача на отыскание
максимума целевой функции, то линию
уровня перемещаем в направлении нормали
до опорной прямой. Эта прямая проходит
через точку пересечения прямых, ограничивающих
область допустимых решений и соответствующих
неравенствам (2) и (3). Определяем координаты
точки
пересечения прямых, ограничивающих
область допустимых решений и соответствующих
неравенствам (2) и (3). Определяем координаты
точки ,
решая систему
,
решая систему .Получим
.Получим .
Подставляя найденные значения переменных
в целевую функцию, получим
.
Подставляя найденные значения переменных
в целевую функцию, получим .
.

Ответ:
 .
.
Симплексный метод
Симплексный метод основывается на следующем:
- область допустимых решений задачи линейного программирования является выпуклым множеством с конечным числом угловых точек, т.е. многогранником или многоугольным множеством;
- оптимальным решением задачи линейного программирования является одна из угловых точек области допустимых решений;
- угловые точки области допустимых решений алгебраически представляют некоторые базисные (опорные) решения системы ограничений задачи.
Данный метод состоит в целенаправленном переборе опорных решений задачи линейного программирования. Он позволяет за конечное число шагов расчета либо найти оптимальное решение, либо установить его отсутствие.
Алгоритм решения задач симплексным методом:
1. Математическая модель задачи должна быть канонической, в противном случае ее необходимо привести к каноническому виду.
Если все ограничения задачи заданы уравнениями и переменные xi неотрицательные, то модель такого вида называется канонической.
2. Находим исходное опорное решение и проверяем его на оптимальность, для чего заполняем симплексную таблицу. Все строки таблицы 1-го шага, за исключением строки Dj (индексная строка), заполняется по данным системы ограничений и целевой функции.
Симплексная таблица имеет следующий вид:
|
сi |
Базисная переменная (БП) |
c1 |
c2 |
… |
cm |
cm+1 |
… |
cn |
L(x) |
|
x1 |
x2 |
… |
xm |
xm+1 |
… |
xn |
bi | ||
|
c1 |
x1 |
1 |
0 |
… |
0 |
h1,m+1 |
… |
h1n |
f1 |
|
c2 |
x2 |
0 |
1 |
… |
0 |
h2,m+1 |
… |
h2n |
f2 |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
cm |
xm |
0 |
0 |
… |
1 |
hm,m+1 |
… |
hmn |
fm |
|
|
∆j |
0 |
0 |
… |
0 |
∆m+1 |
… |
∆n |
L(x1) |
Индексная строка (∆j) для переменных находится по формуле


и по формуле
При этом возможны следующие случаи решения задачи на максимум:
-
если все оценки ∆j
 0, то найденное решение оптимальное;
0, то найденное решение оптимальное;
-
если хотя бы одна оценка ∆j
 0, но при соответствующей переменной
нет ни одного положительного коэффициента,
то решение задачи завершается, так как
L(x)
0, но при соответствующей переменной
нет ни одного положительного коэффициента,
то решение задачи завершается, так как
L(x) ,
т.е. целевая функция не ограничена в
области допустимых решений;
,
т.е. целевая функция не ограничена в
области допустимых решений;
- если хотя бы одна оценка отрицательная, а при соответствующей переменной есть хотя бы один положительный коэффициент, то нужно перейти к другому опорному решению;
- если отрицательных оценок в индексной строке несколько, то в столбец базисной переменной (БП) вводят ту переменную, которой соответствует наибольшая по абсолютной величине отрицательная оценка. Столбец соответствующий этой переменной называется ключевым. За ключевую строку принимают ту, которой соответствует минимальное отношение свободных членов (bi) к положительным коэффициентам k-го столбца. Элемент, находящийся на пересечении ключевых строки и столбца, называют ключевым элементом.
3. Симплексная таблица 2-го шага заполняется следующим образом:
- переписываем ключевую строку, разделив ее элементы на ключевой элемент;
- заполняем базисные столбцы;
- остальные коэффициенты таблицы находим по правилу
“прямоугольника”. Оценки можно считать по приведенным выше формулам или по правилу “прямоугольника”. Получаем новое опорное решение, которое проверяем на оптимальность и т.д.
Примечание:
1. Если целевая функция требует нахождение минимального значения, то критерием оптимальности задачи является неположительность оценок.
Правило “прямоугольника”: пусть ключевым элементом 1-го шага является элемент 1-й строки (m+1)-го столбца – элемент h1,m+1. Тогда элемент i-й строки (m+2)-го столбца 2-го шага, который обозначим
 ,
по правилу “прямоугольника” определяется
по формуле
,
по правилу “прямоугольника” определяется
по формуле
 =
(h1,m+1
=
(h1,m+1 )
/ h1,m+1,
)
/ h1,m+1,
где h1,m+1, hi,m+1, hi,m+2 – элементы 1-го шага.
Пример. Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов и амортизация оборудования за один месяц и общий ресурс при каждом способе производства заданы в таблице (в ден.ед.)
|
Производственный ресурс |
Расход ресурсов за 1 месяц при работе |
Общий ресурс | |
|
по 1 способу |
по 2 способу | ||
|
Сырье |
1 |
2 |
4 |
|
Оборудование |
1 |
1 |
3 |
|
Электроэнергия |
2 |
1 |
8 |
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором – 4 тыс. изделий.
Сколько месяцев должно работать предприятие по каждому из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?
Решение. Пусть x1 – время работы предприятия по первому способу;
x2 – время работы предприятия по второму способу.
Математическая модель задачи примет вид:
L(x)
= 3
x1
+ 4
x2
 max
max
x1
+ 2
x2

x1
+
x2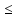 3,
3,
2
x1
+
x2
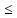 8,
8,
x1 ,
x2
,
x2 .
.
Приведем задачу к каноническому виду:
L(x)
= 3
x1
+ 4
x2
 max
max
x1
+ 2
x2
 x3
x3

x1
+
x2 3,
3,
2
x1
+
x2
 8,
8,
xj ,
j=
1;2;3;4;5.
,
j=
1;2;3;4;5.
Симплексная таблица 1-го шага будет иметь вид:
|
ci |
БП |
3 |
4 |
0 |
0 |
0 |
L(x) | ||||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
bi | ||||||||
|
0 |
x3 |
1 |
2 |
1 |
0 |
0 |
4 | ||||||
|
0 |
x4 |
1 |
1 |
0 |
1 |
0 |
3 | ||||||
|
0 |
x5 |
2 |
1 |
0 |
0 |
1 |
8 | ||||||
|
|
-3 |
-4 |
0 |
0 |
0 |
0 | |||||||
 =
(0,
0, 4, 3, 8),
L(x)
= 0.
=
(0,
0, 4, 3, 8),
L(x)
= 0.
В
индексной строке
 имеются две отрицательные оценки,
значит, найденное решение не является
оптимальным и его можно улучшить. В
качестве ключевого столбца следует
принять столбец базисной переменной
x2
имеются две отрицательные оценки,
значит, найденное решение не является
оптимальным и его можно улучшить. В
качестве ключевого столбца следует
принять столбец базисной переменной
x2 а
за ключевую строку – строку переменной
x3
а
за ключевую строку – строку переменной
x3 где min
(4/2, 3/1, 8/1) = min
(2, 3, 8) = 2.
где min
(4/2, 3/1, 8/1) = min
(2, 3, 8) = 2.
Ключевым элементом является – 2. Вводим в столбец БП переменную x2, выводим x3. Симплексная таблица 2-го шага будет иметь вид:
|
ci |
БП |
3 |
4 |
0 |
0 |
0 |
L(x) | ||||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
bi | ||||||||
|
4 |
x2 |
1/2 |
1 |
1/2 |
0 |
0 |
2 | ||||||
|
0 |
x4 |
1/2 |
0 |
-1/2 |
1 |
0 |
1 | ||||||
|
0 |
x5 |
3/2 |
0 |
-1/2 |
0 |
1 |
6 | ||||||
|
|
-1 |
0 |
2 |
0 |
0 |
8 | |||||||
 =
(0, 2, 0, 1, 6), L(x)
= 8.
=
(0, 2, 0, 1, 6), L(x)
= 8.
В индексной строке имеется одна отрицательная оценка, значит полученное решение можно улучшить. Ключевым элементом является – 1/2. Симплексная таблица 3-го шага будет иметь вид:
|
ci |
БП |
3 |
4 |
0 |
0 |
0 |
L(x) | ||||||
|
x1 |
x2 |
x3 |
x4 |
x5 |
bi | ||||||||
|
4 |
x2 |
0 |
1 |
1 |
-1 |
0 |
1 | ||||||
|
3 |
x1 |
1 |
0 |
-1 |
2 |
0 |
2 | ||||||
|
0 |
x5 |
0 |
0 |
1 |
-3 |
1 |
3 | ||||||
|
|
0 |
0 |
1 |
2 |
0 |
10 | |||||||
Все
оценки свободных переменных

 следовательно,
найденное решение является оптимальным:
следовательно,
найденное решение является оптимальным:
 =
(2, 1, 0, 0, 3), L(x)
= 10.
=
(2, 1, 0, 0, 3), L(x)
= 10.
Ответ: Максимальный выпуск продукции составит 10 тыс.ед., при этом по первому способу предприятие должно работать 2 месяца, а по второму – 1 месяц.



