
Линейная алгебра и аналитическая геомерия
.PDF
sinθ = ± |
|
|
A×a1 + B × a2 |
+ C ×a3 |
|
. |
(3.23) |
||
|
|
|
|
|
|
|
|||
|
|
A2 |
+ B2 + C2 × |
a2 |
+ a2 |
+ a2 |
|
||
|
|
|
|
|
1 |
2 |
3 |
|
|
Знак «+» в этой формуле следует использовать, если угол ϕ − острый, а знак «-» в случае, если угол ϕ − тупой.
Формула (3.22) позволяет сформулировать условия параллельности и перпендикулярности прямой l и плоскости α . Приведём их в следующей теореме.
Теорема 3.11. Справедливы утверждения
1. Для того чтобы прямая l и плоскость α были перпендикулярны
необходимо и достаточно выполнения равенства
A × a1 + B × a2 + C × a3.
2. Для того чтобы прямая l и плоскость α были параллельны
необходимо и достаточно выполнения равенств
A = B = C . a1 a2 a3
3.2.4. Поверхности второго порядка
Определение 3.38. Поверхностью второго порядка называется множество точек пространства, координаты которых удовлетворяют уравнению
Ax2 + By2 + Cz2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz + J, |
(3.24) |
где A, B, C, D, E, F, G, H , I, J − действительные числа, причём A, |
B, C, D, E, F |
не равны нулю одновременно, т.е. A2 + B2 +C2 + D2 + E2 + F 2 ¹ 0. |
Уравнение |
(3.24) называется общим уравнением поверхности второго порядка. Определение 3.39. Поверхность второго порядка, заданная общим
уравнением |
(3.24), называется |
невырожденной, если является |
|
невырожденной матрица |
|
|
|
|
æ A |
D |
E ö |
|
ç |
B |
÷ |
|
çD |
F ÷. |
|
|
ç |
F |
÷ |
|
è E |
C ø |
|
Существует девять типов невырожденных поверхностей второго порядка, канонические уравнения которых можно получить из общего уравнения (3.24) с помощью специальных преобразований системы координат (таблица 2).
Таблица 2
Наименование |
Каноническое уравнение |
|
невырожденной поверхности |
||
поверхности второго порядка |
||
второго порядка |
||
|
Эллипсоиды |
x2 |
+ |
y2 |
+ |
z2 |
= 1 |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
71
PDF created with pdfFactory Pro trial version www.pdffactory.com
Однополостные |
|
x2 |
+ y2 |
− z2 |
= 1 |
||||||
гиперболоиды |
|
a2 |
|
b2 |
|
|
|
c2 |
|
|
|
Двуполостные |
|
x2 |
+ y2 |
− z2 |
= −1 |
||||||
гиперболоиды |
|
a2 |
|
b2 |
|
|
|
c2 |
|
|
|
Эллиптические цилиндры |
|
x2 |
+ |
y2 |
|
= 1 |
|
|
|||
a2 |
b2 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||
Гиперболические цилиндры |
|
x2 |
− |
y2 |
|
= 1 |
|
|
|||
a2 |
b2 |
|
|
||||||||
|
|
|
|
|
|
|
|
||||
Параболические цилиндры |
|
x2 |
= 2 py |
|
|||||||
Эллиптические |
|
z = ax2 + by2 , |
a > 0, b > 0 |
||||||||
параболоиды |
|
|
|
|
|
|
|
|
|
|
|
Гиперболические |
|
z = −ax2 |
+ by2 , a > 0, b > 0 |
||||||||
параболоиды |
|
|
|
|
|
|
|
|
|
|
|
Конусы второго порядка |
|
x2 |
+ |
y2 |
|
− |
z2 |
|
= 0 |
||
a2 |
b2 |
|
|||||||||
|
|
|
|
|
c2 |
|
|||||
Некоторые поверхности второго порядка, как мы увидим ниже, могут быть получены с помощью вращения линий.
Определение 3.40. Вращением линии γ на угол ϕ = 2π около прямой l называется такое движение, при котором каждая точка линии γ описывает окружность с центром на прямой l, лежащую в плоскости,
перпендикулярной прямой l. При этом прямая l называется осью вращения, а поверхность Φ, образованная вращением линии γ
называется поверхностью вращения.
Далее рассмотрим пять классов, включающих в себя все девять невырожденных поверхностей второго порядка. К некоторым из них применим метод сечений, состоящий в определении типа линий пересечения поверхности с координатными плоскостями xOy, xOz, yOz.
Определение 3.41. Главными сечениями поверхности называются линии пересечения этой поверхности с координатными плоскостями xOy, xOz, yOz.
3.2.4.1. Эллипсоиды
Определение 3.42. Эллипсоидом называется поверхность второго порядка, каноническое уравнение которой имеет вид
x2 |
+ |
y2 |
+ |
z2 |
= 1, |
(3.25) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
где a, b, c − положительные постоянные, называемые полуосями.
72
PDF created with pdfFactory Pro trial version www.pdffactory.com

Очевидно, |
что | x |≤ a, |
| y |≤ b, | z |≤ c, т.е. |
эллипсоид |
– |
конечная, |
|
ограниченная |
поверхность. |
Координатные |
плоскости |
xOy, |
xOz, |
yOz |
являются плоскостями симметрии, а начало координат – центром симметрии (центр эллипсоида).
|
Очевидно, главными сечениями |
эллипсоида являются |
эллипсы |
||||||||||
x2 |
+ |
y2 |
= 1 в плоскости xOy, |
x2 |
+ |
z2 |
|
= 1 в плоскости xOz, |
y 2 |
+ |
z2 |
= 1 в |
|
a2 |
b2 |
a2 |
c2 |
b2 |
c2 |
||||||||
|
|
|
|
|
|
||||||||
плоскости yOz. Уравнения этих кривых второго порядка получаются, если в
уравнении (3.25) положить поочерёдно z = 0, |
y = 0, x = 0 соответственно. |
|||||||||||||||||||||||||||
Определим |
тип линий |
|
пересечения |
|
|
эллипсоида с |
плоскостями |
|||||||||||||||||||||
x = const, y = const |
и z = const, |
параллельными |
|
|
координатным |
плоскостям |
||||||||||||||||||||||
xOy, xOz и yOz соответственно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим |
линию пересечения |
|
эллипсоида |
с плоскостью z = h, |
||||||||||||||||||||||||
параллельной плоскости xOy. |
Для этого положим в уравнении (3.25) z = h, в |
|||||||||||||||||||||||||||
результате чего получится |
|
|
x2 |
|
|
|
|
|
y2 |
|
|
|
|
h2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
+ |
|
= 1- |
|
, |
|
|
|
|
|
|
|
|
|||||||||||
или |
|
|
|
|
a2 |
b2 |
|
c2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
= 1, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
æ |
|
|
h2 |
ö |
æ |
|
|
|
|
h |
2 |
ö |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ça |
1- |
|
|
÷ |
|
|
|
çb 1 |
- |
|
|
|
|
÷ |
|
|
|
|
|
|
||||||
|
c2 |
|
|
|
|
c |
|
|
|
|
|
|
|
|||||||||||||||
|
ç |
|
|
÷ |
|
|
|
ç |
|
|
|
|
2 |
÷ |
|
|
|
|
|
|
||||||||
|
è |
|
|
|
ø |
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
т.е. получается эллипс с полуосями a |
|
1- |
h2 |
|
и b 1- |
h2 |
. Таким образом, при |
|||||||||||||||||||||
|
c2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
||||
h = 0 получится эллипс с полуосями a и b; |
при увеличении | h | |
этот эллипс |
||||||||||||||||||||||||||
будет подобно уменьшаться и при | h |= c полуоси станут равными нулю, т.е. эллипс выродится в точку. Пересечение эллипсоида с плоскостями y = h и x = h даёт аналогичный результат, и мы получаем поверхность, изображённую на рис. 22, называемую также трёхосным эллипсоидом.
z
y
x
Рисунок 22. Эллипсоид
73
PDF created with pdfFactory Pro trial version www.pdffactory.com
Если две из полуосей равны, например, a = b, то в сечении с
плоскостями z = h будут получаться окружности. Тогда вместо трёхосного эллипсоида получим так называемый эллипсоид вращения, т.е. поверхность, образованная вращением эллипса вокруг одной из его осей:
x2 |
+ |
y2 |
+ |
z2 |
|
a2 |
a2 |
c2 |
|||
|
|
||||
x2 |
+ |
y2 |
+ |
z2 |
|
a2 |
b2 |
a2 |
|||
|
|
||||
x2 |
+ |
y2 |
+ |
z2 |
|
a2 |
b2 |
b2 |
|||
|
|
=1 − эллипсоид вращения с осью вращения Oz,
=1 −эллипсоид вращения с осью вращения Oy,
=1 − эллипсоид вращения с осью вращения Ox.
В зависимости от того, вокруг какой оси – большой или малой – будет производиться вращение эллипса, получится «вытянутый» или «сплюснутый» эллипсоид вращения.
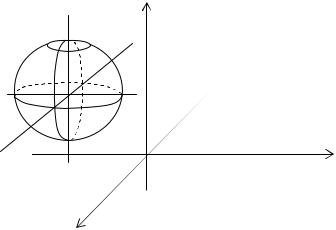
Если же все три полуоси эллипсоида равны, то он превращается в сферу (рис. 23).
z
O |
y |
x
Рисунок 23. Сфера
Отметим тот факт, что трёхосный эллипсоид получается в результате
двух равномерных сжатий или растяжений сферы к координатным плоскостям; в результате же одного сжатия сферы получится эллипсоид вращения.
3.2.4.2. Гиперболоиды
Гиперболоиды бывают двух типов – однополостные и двуполостные.
Определение 3.43. Однополостным гиперболоидом называется поверхность второго порядка, каноническое уравнение которой имеет вид
x2 |
+ |
y2 |
− |
z2 |
= 1, |
|
a2 |
b2 |
c2 |
||||
|
|
|
где a, b, c − положительные постоянные, называемые полуосями.
74
PDF created with pdfFactory Pro trial version www.pdffactory.com
Очевидно, что | x |£ a, | y |£ b, | z |³ c, т.е. однополостный гиперболоид –
бесконечная, неограниченная поверхность.
Сечение однополостного гиперболоида плоскостью z = h даёт эллипс с
|
|
|
|
|
|
|
|
|
|
|
полуосями a |
1+ |
h2 |
|
и b |
1+ |
h2 |
. Следовательно, при |
h = 0 получится эллипс с |
||
c2 |
c2 |
|||||||||
|
|
|
|
|
|
|
||||
полуосями a |
и b, |
а |
при |
увеличении | h | этот |
эллипс будет подобно |
|||||
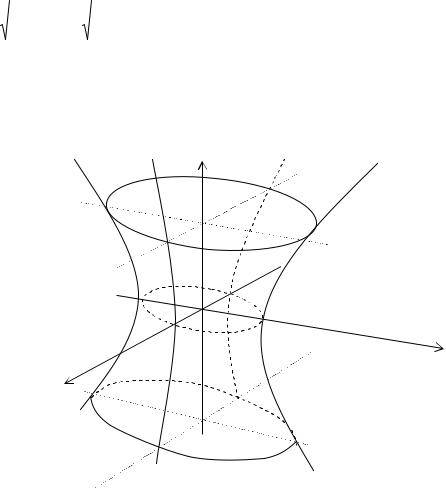
увеличиваться до бесконечности. Пересечение однополостного гиперболоида с плоскостями y = h и x = h даёт гиперболы, и мы получаем поверхность, изображённую на рис. 24.
z
O
x |
y |
Рисунок 24. Однополостный гиперболоид
Как и эллипсоид, однополостный гиперболоид имеет три плоскости симметрии и центр симметрии.
Если a = b, то получится однополостный гиперболоид вращения – поверхность, образованная вращением гиперболы вокруг её мнимой оси:
x2 |
+ |
y2 |
− |
z2 |
= 1. |
|
a2 |
a2 |
c2 |
||||
|
|
|
Определение 3.44. Двуполостным гиперболоидом называется поверхность второго порядка, каноническое уравнение которой имеет вид
x2 |
+ |
y2 |
− |
z2 |
= −1, |
|
a2 |
b2 |
c2 |
||||
|
|
|
где a, b, c − положительные постоянные, называемые полуосями.
75
PDF created with pdfFactory Pro trial version www.pdffactory.com

Сечение двуполостного гиперболоида плоскостью z = h даёт эллипс с
|
|
|
|
|
|
|
|
полуосями a |
h2 |
−1 и b |
h2 |
−1. Таким образом, при | h |< c сечения нет, при |
|||
c2 |
c2 |
||||||
|
|
|
|
|
|||
| h |= c получаются нулевые полуоси, а при дальнейшем увеличении | h | −
эллипс, подобно увеличивающийся до бесконечности. Пересечение двуполостного гиперболоида с плоскостями y = h и x = h даёт гиперболы, и
мы получаем поверхность, изображённую на рис. 25, и состоящую из двух бесконечных частей, одна из которых ограничена снизу, а другая – сверху.
z
O
y
x
Рисунок 25. Двуполостный гиперболоид
Если a = b, то получится двуполостный гиперболоид вращения –
поверхность, образованная вращением гиперболы вокруг её действительной оси:
x2 |
+ |
y2 |
− |
z2 |
= −1. |
|
a2 |
a2 |
c2 |
||||
|
|
|
3.2.4.3. Цилиндрические поверхности
Определение 3.45. Связкой параллельных прямых называется множество G(l) прямых пространства, параллельных одной и той же прямой l,
называемой осью связки.
Определение 3.46. Цилиндрической поверхностью (цилиндром) Φ называется множество точек пространства, принадлежащих тем прямым связки параллельных прямых G(l), которые пересекают некоторую кривую
76
PDF created with pdfFactory Pro trial version www.pdffactory.com

второго порядка γ . При этом кривая γ |
называется направляющей |
поверхности Φ, а прямые связки G(l), |
пересекающие кривую γ , − |
образующими поверхности Φ.
Любое уравнение F(x, y) = 0 второго порядка является в пространстве
уравнением некоторой цилиндрической поверхности с направляющей кривой второго порядка γ , лежащей в плоскости xOy, и имеющей то же
уравнение F(x, y) = 0, и образующими, параллельными оси аппликат.
Ниже рассмотрим некоторые частные случаи цилиндрических
поверхностей, направляющие которых |
лежат в |
плоскости xOy, а |
|||
образующие параллельны оси Oz. |
|
|
|
|
|
Уравнение |
|
|
|
|
|
|
x2 |
+ |
y2 |
= 1 |
|
|
a2 |
b2 |
|
||
|
|
|
|
||
определяет в пространстве эллиптический цилиндр – цилиндрическую поверхность, направляющая которой – эллипс γ в плоскости xOy (рис. 26).
z
y
O
γ : |
x2 |
+ |
y2 |
= 1 |
|
a2 |
b2 |
||||
|
|
|
x
Рисунок 26. Эллиптический цилиндр
Уравнение
x2 |
− |
y2 |
= 1 |
|
a2 |
b2 |
|||
|
|
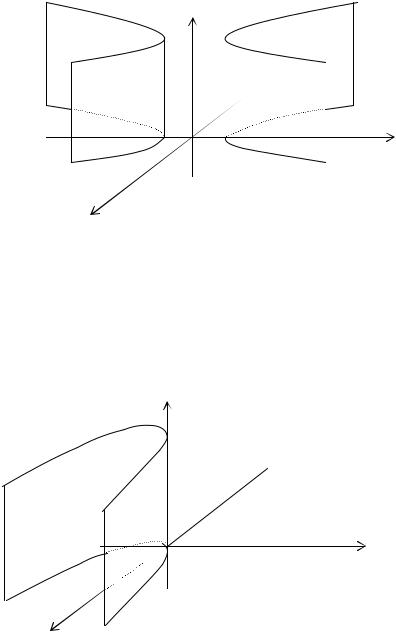
определяет в пространстве гиперболический цилиндр – цилиндрическую поверхность с направляющей гиперболой γ в плоскости xOy (рис. 27).
77
PDF created with pdfFactory Pro trial version www.pdffactory.com
z
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
||
O |
|
|
|
y2 |
|
||
|
|
|
x2 |
|
|
||
|
γ : |
− |
= 1 |
||||
a2 |
b2 |
||||||
|
|
|
|
|
|||
x
Рисунок 23. Гиперболический цилиндр
Уравнение
x2 = 2 py
определяет в пространстве параболический цилиндр – цилиндрическую поверхность с направляющей параболой γ в плоскости xOy (рис. 28).
z
y
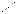
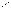 O
O
γ : x2 = 2 py
x
Рисунок 28. Параболический цилиндр
3.2.4.4. Параболоиды
Параболоиды бывают двух типов – эллиптические и гиперболические.
Определение 3.47. Эллиптическим параболоидом называется поверхность второго порядка, каноническое уравнение которой имеет вид z = ax2 + by2 ,
78
PDF created with pdfFactory Pro trial version www.pdffactory.com
где a, b − положительные постоянные.
В пересечении с плоскостью z = h получится
ax2 + by2 |
= h |
|
или |
x2 |
+ |
y2 |
= 1, |
|||||
|
|
h |
|
|||||||||
|
|
|
|
|
|
|
|
h |
|
|||
|
|
|
|
|
|
a |
|
|
|
b |
|
|
|
|
|
|
|
|
|||||||
т.е. эллипс с полуосями |
h |
и |
h |
. Следовательно, |
при h < 0 пересечения |
|||||||
|
a |
|
b |
|
|
|
|
|
|
|
|
|
не будет, при h = 0 получится точка O, а при увеличении h > 0 получится
эллипс, подобно увеличивающийся до бесконечности. Пересечение эллиптического параболоида с плоскостями y = h и x = h даёт параболы, и мы получаем поверхность, изображённую на рис. 29.
z
O |
y |
x
Рисунок 29. Эллиптический параболоид
Эллиптический параболоид имеет две плоскости симметрии ( xOz и yOz ). Если a = b, то получается эллиптический параболоид вращения – поверхность, образованная вращением параболы вокруг её оси:
z = a(x2 + y2 ).
Определение 3.48. Гиперболическим параболоидом называется поверхность второго порядка, каноническое уравнение которой имеет вид z = −ax2 + by2 ,
где a, b − положительные постоянные.
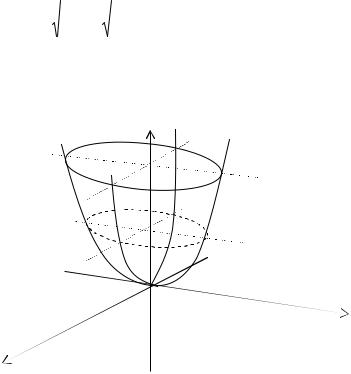
Пересечение гиперболического параболоида с плоскостью yOz даёт параболу z = by2 , обращённую ветвями вверх, тогда как его пересечение с плоскостями y = h даёт параболы z = −ax2 + bh2 , обращённые ветвями вниз.
Пересечение же этого параболоида с плоскостями |
z = h даёт гиперболы |
||||||||
|
x2 |
− |
y2 |
= −1. Таким образом получается поверхность, |
имеющая вид седла |
||||
|
|
h |
|
||||||
|
|
|
|
h |
|
|
|||
|
|
a |
|
|
|
b |
|
|
|
(рис. 30).
79
PDF created with pdfFactory Pro trial version www.pdffactory.com
z
O
x 
y
Рисунок 30. Гиперболический параболоид
3.2.4.5. Конусы второго порядка
Определение 3.49. Конусом второго порядка (конической поверхностью второго порядка) называется поверхность второго порядка, каноническое
уравнение которой имеет вид
|
x2 |
+ |
y2 |
- |
z2 |
= 0, |
(3.26) |
|
a2 |
b2 |
c2 |
||||
|
|
|
|
|
|||
где a, b, c − положительные постоянные. |
|
|
|
|
|||
Положив в уравнении (3.26) |
поочерёдно z = 0, |
y = 0, x = 0, получим |
|||||
главные сечения конуса второго порядка: точку O в плоскости xOy,
называемую вершиной конуса; пару пересекающихся прямых |
|
x2 |
- |
z2 |
= 0 в |
|||||||
|
a2 |
c2 |
||||||||||
|
|
|
|
y 2 |
|
z2 |
|
|
|
|
||
плоскости xOz; пару пересекающихся прямых |
|
- |
= 0 в плоскости yOz. |
|||||||||
|
b2 |
|
||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
||
Определим |
тип линий |
пересечения |
эллипсоида с плоскостями |
|||||||||
x = const, y = const |
и z = const, |
параллельными |
|
координатным |
плоскостям |
|||||||
xOy, xOz и yOz соответственно, |
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим |
линию пересечения эллипсоида с плоскостью |
z = h, |
||||||||||
параллельной плоскости xOy. Для этого положим в уравнении (3.26) z = h, в
результате чего получится
x2 |
+ |
y2 |
= h2 |
, |
или |
|
a2 |
b2 |
|||||
|
c2 |
|
|
т.е. получается эллипс с полуосями
|
|
|
x2 |
|
|
+ |
|
æ a | h |ö2 |
|
||||
|
ç |
|
|
÷ |
|
|
|
|
c |
|
|
||
|
è |
|
ø |
|
|
|
a | h | |
и |
b | h | |
; |
|||
c |
|
|
c |
|
|
|
|
y2 |
|
= 1, |
|
æ b | h | ö2 |
||||
ç |
|
÷ |
|
|
c |
||||
è |
ø |
|
||
| h | этот
эллипс будет подобно увеличиваться до бесконечности, а при |
уменьшении | h | − подобно уменьшаться. |
80
PDF created with pdfFactory Pro trial version www.pdffactory.com
