
Линейная алгебра и аналитическая геомерия
.PDF
Определение 2.3. Длиной вектора AB называется расстояние между началом и концом вектора. Длиной вектора называется длина отрезка AB.
Длина вектора обозначается через | AB | или | a |.
Определение 2.4. Векторы называются коллинеарными, если они как
направленные отрезки лежат на одной прямой или на параллельных прямых.
|
Факт коллинеарности векторов |
a и |
b |
обозначается записью вида |
|||||||
a || |
|
. При этом коллинеарные |
векторы |
могут быть |
одинаково |
||||||
b |
|||||||||||
направленными ( a −− |
|
) и противоположно |
направленными |
( a −↓ |
|
). |
|||||
b |
b |
||||||||||
Нулевой вектор коллинеарен любому вектору.
Определение 2.5. Векторы называются компланарными, если существует плоскость, которой они параллельны.
Замечание. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.
Определение 2.6. Векторы называются равными, если они одинаково направлены и имеют одинаковые длины, т.е. a = b a −− b и | a |=| b | .
Все векторы можно привести к общему началу, т.е. построить векторы, соответственно равные данным и имеющие общее начало. Из определения 2.6, в частности, следует, что любой вектор имеет бесконечно много векторов, равных ему.
Определение 2.7. Линейными операциями над векторами называется сложение векторов a + b.и умножение вектора на число (скаляр) α × a.
Вектор a одинаково направлен (противоположно направлен) с вектором α × a,если α > 0 (α < 0).
Теорема 2.1. Линейные операции с векторами обладают следующими свойствами:
1.a + b = b + a, т.е. операция сложения векторов коммутативна.
|
(a + |
|
|
) + |
|
|
= a + ( |
|
+ с), |
|
|
|
||||||
2. |
b |
с |
b |
т.е. |
операция |
сложения векторов |
||||||||||||
ассоциативна. |
|
|
|
|
|
|
|
|||||||||||
3. |
a + |
|
= a, т.е. операция |
|
сложения |
векторов |
нейтральна |
|||||||||||
0 |
|
|||||||||||||||||
относительно нулевого вектора. |
|
|
|
|
|
|
|
|||||||||||
4. |
a + (−a) = |
|
|
для |
|
любого |
вектора a |
существует |
||||||||||
0, т.е. |
|
|||||||||||||||||
противоположный вектор − a. |
|
|
|
|
|
|
|
|||||||||||
5. |
(α × β ) × a = α × (β × a), |
т.е. |
операция |
умножения |
вектора на |
|||||||||||||
число ассоциативна. |
|
|
|
|
|
|
|
|||||||||||
6. |
(α + β ) × a = α × a + β × a, |
т.е. |
операция умножения вектора на |
|||||||||||||||
число дистрибутивна относительно сложения чисел.
31
PDF created with pdfFactory Pro trial version www.pdffactory.com

7. |
α × (a + |
|
) = α × a + α × |
|
, т.е. операция умножения |
вектора на |
|
b |
b |
||||||
число дистрибутивна относительно сложения векторов. |
|
||||||
8. |
1 |
× a = a, т.е. т.е. операция умножения вектора |
на число |
||||
нейтральна |
относительно единицы. |
|
|||||
Определение 2.8. Базисом системы векторов в пространстве будем называть любую тройку некомпланарных векторов {e1, e2 , e3}, взятых в определённом порядке. Базисом системы векторов на плоскости будем называть любую пару неколлинеарных векторов {e1, e2} , взятых в определённом порядке.
Определение |
2.9. Если {e1, e2 , e3} |
- |
базис системы |
векторов в |
||||
пространстве и a = α ×e1 + β × e2 + γ × e3 , |
то числа α, β и γ |
называются |
||||||
компонентами |
или координатами |
вектора |
a |
в этом базисе. При |
этом |
|||
используют запись вида: |
a = (α, β ,γ ). |
|
|
|
|
|
||
Аналогично определяются координаты векторов на плоскости. |
|
|||||||
Теорема 2.2. Справедливы следующие свойства: |
|
|
||||||
1. Равные |
векторы |
имеют |
одинаковые |
координаты, |
т.е., |
если |
||
a = (α1, β1, γ1 ), b = (α2 , β2 , γ 2 ) и a = b , то α1 = α2 , β1 = β2 , γ1 = γ 2 .
2. При умножении вектора на число его координаты умножаются на это
число, т.е., если a = (α, β ,γ ), |
то k × a = (k ×α, k × β , k ×γ ). |
|
||||||||
3. При сложении |
векторов складываются |
их |
соответствующие |
|||||||
координаты, т.е., если a = (α1 , β1, γ1 ), |
|
|
= (α2 , β2 , γ 2 ) , то |
|
||||||
b |
|
|||||||||
|
|
a = (α1 +α2 , β1 + β2 , γ1 +γ 2 ). |
|
|
||||||
Определение 2.10. Векторы |
a1, a2 ,K, an |
называются линейно |
||||||||
зависимыми, |
если |
существует |
|
такая |
линейная |
комбинация |
||||
α1 × a1 + α2 × a2 +K+ αn × an = |
|
|
|
|
|
|||||
0 |
при |
одновременно |
не |
равных нулю |
||||||
α1, α2 ,K,αn . Если же указанное векторное равенство выполняется только
при α1 = α2 = K = αn = 0, то векторы называются линейно независимыми. Теорема 2.3. Справедливы следующие свойства:
1. Если среди векторов a1, a2 ,K, an есть нулевой, то эти векторы линейно зависимы.
2.Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.
3.Система векторов линейно зависима тогда и только тогда, когда
один из векторов представим в виде линейной комбинации остальных векторов.
32
PDF created with pdfFactory Pro trial version www.pdffactory.com

4.Любые два коллинеарных вектора линейно зависимы и, наоборот, любые два линейно зависимых вектора коллинеарны.
5.Любые три компланарных вектора линейно зависимы и, наоборот, любые три линейно зависимых векторы компланарны.
6.Векторы, образующие базис, линейно независимы.
Пример. Векторы a = (1, 2, 3), |
|
= (−1, 0, 3), |
с = (2, 1, −1), |
|
|
= (3, 2, 2) |
|
b |
d |
||||||
заданы в некотором базисе. Покажем, что |
векторы a, |
|
и с сами |
||||
b |
|||||||
образуют базис и найдём координаты вектора d в этом базисе.
Векторы, образующие базис, линейно независимы, т.е. существуют, и притом единственные, такие действительные числа α, β, γ , что
d = α × a + β ×b + γ × c. В координатной форме последнее равенство принимает
вид системы линейных алгебраических уравнений
ì α - β + 2γ = 3, ïí2α + γ = 2,
ïî3α + 3β - γ = 2.
Определитель основной матрицы этой системы отличен от нуля:
1 -1 2
20 1 = 4 ¹ 0,
33 -1
т.е. существует единственное решение системы α, β, γ , а значит, векторы
a, |
b |
и с образуют базис. Вычислим значения α, |
β , γ методом Крамера: |
|||||||||||||||||||||||||
1 = |
|
3 |
|
|
|
-1 |
2 |
|
|
|
= -1, α = |
D1 |
|
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 0 |
1 |
|
|
|
= - |
; |
|||||||||||||||||||||
|
|
|
|
D |
4 |
|||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
3 |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 = |
|
1 |
3 |
2 |
|
|
|
|
|
|
β = |
|
|
D2 |
|
|
|
7 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 2 1 |
= 7, |
|
|
|
|
|
= |
; |
|
||||||||||||||||||
|
|
|
|
|
D |
|
4 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
2 |
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 = |
|
1 |
-1 |
3 |
|
|
|
|
γ = |
|
D3 |
|
|
|
5 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
0 |
2 |
|
= 10, |
|
|
|
|
= |
. |
|
||||||||||||||||
|
|
|
|
D |
|
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
Таким образом, вектор d |
в базисе a, b , |
с имеет координаты: |
||||||||||||||||||||||||||
d = (−1/ 4, 7 / 4,5 / 2).
2.2. Система координат
Для определения однозначного положения произвольной точки могут использоваться различные системы координат. Понятие системы
33
PDF created with pdfFactory Pro trial version www.pdffactory.com
координат представляет собой совокупность точки начала отсчёта (начала координат) и некоторого базиса. Как на плоскости, так и в пространстве, возможно задание самых разнообразных систем координат. Выбор системы координат зависит от характера поставленной геометрической, физической или технической задачи. Рассмотрим некоторые наиболее часто применяемые на практике системы координат.
2.2.1. Декартова система координат
Зафиксируем в пространстве (на плоскости) точку О и рассмотрим
произвольную точку М. Вектор ОМ назовём радиус-вектором точки М. Если в пространстве (на плоскости) задать некоторый базис {e1, e2 , e3}
({e1, e2}), то точке М можно сопоставить некоторую тройку чисел (пару чисел) – координаты её радиус–вектора.
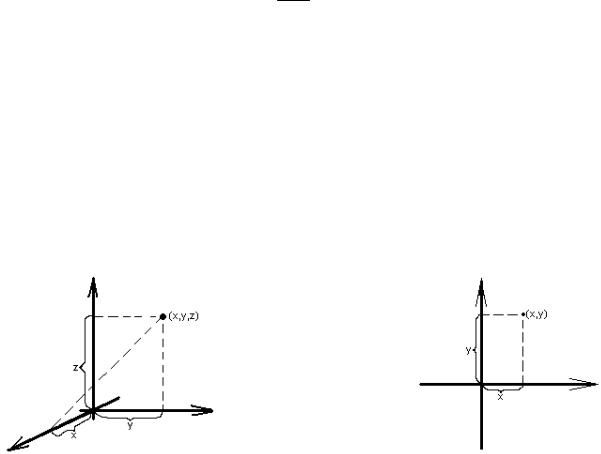
Определение 2.11. Декартовой системой координат в пространстве (на плоскости) называется совокупность точки О и базиса {e1, e2 , e3} ({e1, e2} ).
Точка О называется началом координат. Прямые, проходящие через начало координат, называются осями координат: первая ось (соотвествует первой координате) называется осью абсцисс, вторая ось (соотвествует второй координате) – осью ординат, третья ось (соотвествует третьей координате и существует только в пространстве) – осью аппликат.
Рисунок 3. Декартова система |
Рисунок 4. Декартова система |
координат в пространстве |
координат на плоскости |
Определение 2.12. Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице.
Определение 2.13. Декартова система координат, базис которой ортонормирован, называется декартовой прямоугольной системой координат.
34
PDF created with pdfFactory Pro trial version www.pdffactory.com

Ортонормированный базис декартовой прямоугольной системы
координат |
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
где |
||||||
|
пространстве – это тройка векторов {i |
, j, k}, |
|||||||||||||||||||
|
|
= (1,0,0), |
|
|
|
|
|
|
|
|
|
|
|
||||||||
i |
j = (0,1, 0), k = (0, 0,1) , на плоскости – это пара векторов {i , |
|
j}, |
||||||||||||||||||
|
|
= (1, 0), |
|
|
|
|
|
||||||||||||||
где i |
j = (0,1) ). |
|
|
|
|||||||||||||||||
2.2.2. Полярная система координат
Суть задания какой-либо системы координат на плоскости состоит в том, чтобы каждой точке М плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. Для того чтобы задать полярную систему координат, надо зафиксировать, во-первых, точку начала координат, а во-вторых, луч, выходящий из этой точки. Необходимо также определить единичный
отрезок и положительное направление отсчёта угла между лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.
В случае использования полярной система координат положение точки на плоскости задаётся двумя числами: расстоянием от точки до начала координат, углом между зафиксированным лучом и отрезком, соединяющим точку и начало координат (рис.5). Обычно направление отсчёта угла выбирают против часовой стрелки. Стандартное обозначение координат точки в полярной системе – (ρ,φ). Очевидно, ρ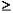 0.
0.
Рисунок 5. Полярная система координат
Существуют формулы перехода между заданными стандартным образом прямоугольной декартовой и полярной системами координат. Если они друг соответствуют другу (т.е. совпадают начала координат в обеих системах, луч полярной системы координат совпадает с «положительной» частью оси абсцисс прямоугольной декартовой системы
координат, |
единичные |
отрезки |
одинаковы), |
то x = ρ × cosϕ, y = ρ × sinϕ; |
|||||
наоборот, |
ρ = |
|
, |
tgϕ = |
y |
. |
С помощью |
этих формул можно |
|
x2 + y2 |
|||||||||
|
|||||||||
|
|
|
|
|
x |
|
|
||
осуществлять переход между двумя системами координат, преобразовывать координаты точек, уравнения кривых и т.д. В других случаях формулы связи зависят от постановки задачи, но получить их легко из геометрических соображений (рис.6):
35
PDF created with pdfFactory Pro trial version www.pdffactory.com
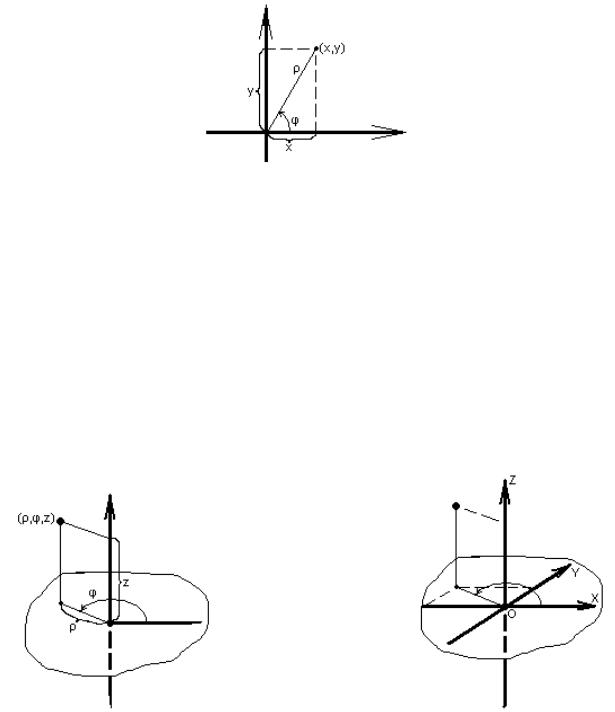
Рисунок 6. Связь полярной и прямоугольной декартовой
систем координат
2.2.3. Цилиндрическая система координат
Цилиндрическая система координат в пространстве – аналог полярной системы координат на плоскости. Для того чтобы получить цилиндрическую систему координат, надо на плоскости ввести полярную систему координат и добавить вертикальную координатную ось. В этом случае координаты точки – три числа: первые два – полярные координаты проекции точки на плоскость, третье – величина проекции точки на вертикальную ось (рис.7).
Рисунок 7. Цилиндрическая |
Рисунок 8. Связь цилиндрической |
система координат |
и прямоугольной декартовой |
|
систем координат |
36
PDF created with pdfFactory Pro trial version www.pdffactory.com
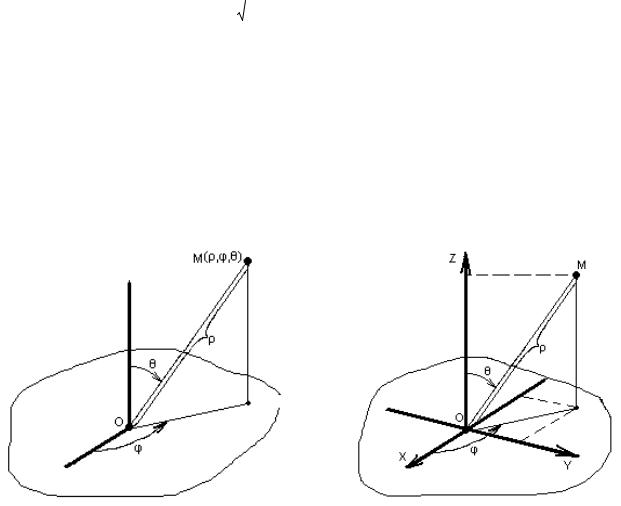
Из геометрических соображений можно получить формулы перехода между цилиндрической и декартовой системами координат. В случае, изображённом на рис. 8, формулы перехода такие:
ìx = ρ × cosϕ,
ïíy = ρ × sinϕ, ïîz = z;
ρ = |
|
, tgϕ = |
y |
|
|
x2 + y2 |
, z = z. |
||||
x |
|||||
|
|
|
|
2.2.4. Сферическая система координат
Сферическая система координат вводится следующим образом: фиксируем плоскость, на ней - точку О начала координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч, лежащий в плоскости. Положение произвольной точки М задаётся тремя числами: расстоянием от точки О до точки М; углом между проекцией отрезка ОМ на плоскость и лежащим в плоскости лучом; углом между перпендикулярным плоскости лучом и отрезком ОМ (рис.9).
Рисунок 9. Сферическая |
Рисунок 10. Связь сферической |
система координат |
и прямоугольной декартовой |
|
систем координат |
Из геометрических соображений, приведённых на рис. 10, можно
получить формулы связи сферической и прямоугольной декартовой системами координат:
37
PDF created with pdfFactory Pro trial version www.pdffactory.com

ìx = ρ × sinθ × cosϕ,
ïíy = ρ × sinθ ×sin ϕ,
ïîz = ρ × cosθ;
|
y |
|
|
|||
ρ = |
x2 + y2 + z2 |
, tgϕ = |
, |
tgθ = |
||
x |
||||||
|
|
|
|
|
||

 x2 + y2 . z
x2 + y2 . z
2.3. Вектор и его длина в координатной форме
Не уменьшая общности результатов, рассмотрим в этом пункте и
далее множество точек прямоугольной декартовой системы координат в
пространстве. |
Если |
точки |
заданы своими |
координатами |
A(xA , yA , zA ), |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a = |
|
равны |
|
||||
B(xB , yB , zB ), |
то |
координаты |
вектора |
AB |
разности |
|||||||||||||
соответствующих |
координат |
конца |
и |
начала вектора, т.е. |
||||||||||||||
a = |
|
= (xB − xA , yB − yA , zB − zA ). При |
|
|
|
|
|
|||||||||||
AB |
этом |
длина этого |
вектора |
|||||||||||||||
вычисляется по формуле |
|
|
|
|
|
|
|
|
|
|||||||||
|
a |
|
= |
|
(xB - xA )2 + (yB - yA )2 + (zB - zA )2 . |
|
||||||||||||
|
|
|
||||||||||||||||
Теорема 2.4. Если точка М делит вектор |
|
(или отрезок AB ) в |
||||||||||||||||
AB |
||||||||||||||||||
отношении λ/μ, то её координаты определяются равенствами: |
|
|||||||||||||||||
|
|
|
xM = |
μxA + λxB , |
|
yM = μyA + λyB , zM |
= μzA + λzB . |
|
||||||||||
|
|
|
|
μ + λ |
|
|
μ + λ |
|
|
μ + λ |
|
|||||||
Из теоремы 2.4 при λ = μ |
|
следует, что координаты середины отрезка |
||||||||||||||||
вычисляются как полусуммы соответствующих координат начала и конца этого отрезка:
xM = |
xA + xB |
, yM |
= |
|
yA + yB |
, |
zM = |
zA + zB |
|
|
|
2 |
|
||||||||
2 |
|
|
|
2 |
|
|
||||
2.4. Скалярное произведение векторов |
|
|
|
|
||||||
Определение 2.12. Скалярным |
|
произведением векторов a и |
|
|||||||
|
b |
|||||||||
называется число, равное произведению длин этих векторов на косинус ϕ угла между ними:
a × b = a × b × cosϕ.
Основные свойства скалярного произведения сформулированы в следующей теореме.
Теорема 2.5. Справедливы следующие утверждения:
1. Скалярный квадрат вектора равен квадрату его длины: a × a = a 2 = a 2 .
38
PDF created with pdfFactory Pro trial version www.pdffactory.com

2. Скалярное произведение векторов равно нулю в том и только в том случае, когда векторы ортогональны или хотя бы один из них нулевой:
|
|
a × |
|
= 0 Û a ^ |
|
, или a = |
|
|
|
|
|
|
|
|
|||||||||||||
b |
b |
0, или b = 0. |
|||||||||||||||||||||||||
3. Скалярное произведение векторов коммутативно: |
|||||||||||||||||||||||||||
|
|
|
|
|
|
a × |
|
|
= |
|
× a. |
|
|
|
|
|
|||||||||||
|
|
|
|
b |
b |
|
|
|
|
|
|||||||||||||||||
4. Скалярное произведение векторов дистрибутивно относительно |
|||||||||||||||||||||||||||
сложения векторов: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
a × ( |
b |
+ |
с |
) = a × |
b |
+ a × с. |
|
|
|
|
|
||||||||||||
5. Скалярное произведение векторов ассоциативно относительно |
|||||||||||||||||||||||||||
умножения вектора на число: |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
(α × a) × |
|
= α × (a × |
|
|
). |
|
|
|
|
|
|||||||||||||
|
|
|
|
b |
b |
|
|
|
|
|
|||||||||||||||||
6. Скалярное произведение векторов равно сумме произведений |
|||||||||||||||||||||||||||
соответствующих координат этих векторов: |
|
|
|
|
|
||||||||||||||||||||||
a × |
|
= a1 × b1 + a2 ×b2 + a3 ×b3 , где a = (a1 , a2 , a3 ), |
|
= (b1 , |
b2 , b3 ). |
||||||||||||||||||||||
b |
b |
||||||||||||||||||||||||||
Используя определение 2.12, утверждение 6 |
теоремы 2.5, а также |
||||||||||||||||||||||||||
формулу длины вектора, получаем формулу для вычисления угла между векторами:
|
a × |
|
|
|
|
|
|
a1 ×b1 |
+ a2 × b2 |
+ a3 |
× b3 |
|
||||
cosϕ = |
b |
|
= |
|
. |
|||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
× |
|
b |
|
|
|
a12 + a22 |
+ a32 × b12 + b22 + b32 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Найти скалярное произведение (5 a + 3 b )×(2 a - b ), если a = 2, b = 3, a ^ b.
Применяя утверждения теоремы 2.5 и определение 2.12, получим: (5 a + 3 b )×(2 a - b )=10× (a × a) - 5× (a ×b ) + 6× (a × b ) - 3× (b ×b ) =
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 10 × |
|
a |
|
2 - 3× |
|
|
|
|
2 = 10 × 23 - 3× 32 = 13, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
Пример. |
Найти |
угол |
между |
векторами |
a |
и |
|
|
|
|
, если |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a = i |
|
+ 2 j + 3k , |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 6i |
+ 4 j - 2k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Векторы a и |
|
|
имеют следующие координаты: a |
= (1, 2, 3), |
|
|
= (6, 4, -2). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда, по утверждению 6 теоремы 2.5, получим |
a × |
|
= 6 + 8 – 6 = 8. Так как |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
= |
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1+ 4 + 9 |
14, |
|
|
36 +16 + 4 |
|
|
|
56, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosϕ = |
8 |
|
|
= |
|
|
|
8 |
|
|
|
|
|
|
= |
4 |
= |
2 |
|
или |
|
|
ϕ = arccos 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
56 |
2 |
14 |
|
14 |
14 |
7 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Пример. |
Найти скалярное |
произведение (3 a |
- 2 |
|
)×(5 a |
- 6 |
|
), если |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
= 4, |
|
|
|
|
= 6, |
|
ϕ = π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Применяя утверждения теоремы 2.5 и определение 2.12, получим: (3 a - 2 b )×(5 a - 6 b )=15× (a × a) - 18× (a × b ) - 10× (a × b ) + 12× (b × b ) =
39
PDF created with pdfFactory Pro trial version www.pdffactory.com

= 15× a 2 - 28× a × b × cos π3 +12 × b 2 = 15×16 - 28× 4 × 6 × 12 +12 ×36 = 336.
Пример. При каком значении m векторы a = mi + j и b = 3i - 3 j - 4k
перпендикулярны?
Запишем координаты векторов a = (m, 1, 0) и b = (3, -3, -4) и применим утверждение 2 теоремы 2.5:
a × b = 3m - 3 = 0 Û m = 1.
Пример. Найти скалярное произведение векторов 2a + 3b + 4c и 5a + 6b + 7c ,
если |
|
a |
|
= 1, |
|
|
|
|
|
|
|
= 2, |
|
c |
|
= 3, |
|
a^ |
|
= a ^ c = |
|
^ c = |
π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
b |
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Применяя утверждения теоремы 2.5, а также определение 2.12, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 2a + 3 |
|
|
+ 4c )× ( 5a + 6 |
|
|
|
+ 7c ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
= 10 × (a × a) +12 × (a × |
|
) +14× (a × c) +15× (a × |
|
) +18× ( |
|
× |
|
) + 21× ( |
|
|
× |
|
) + 20 × (c × a) + |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
b |
b |
b |
c |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
+ 24 × (b × c) + 28× (c × c) = 10 × (a × a) + 27 × (a × |
|
) + 34 × (a × c) + 45× ( |
|
× c) +18× ( |
|
× |
|
) + 28× (c × c) = |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
b |
b |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= 10 ×1 |
|
+ 27 ×1× 2 × |
|
|
|
|
+ 34×1×3× |
|
+ 45 |
× 2 × 3× |
|
+18× 2 |
|
+ 28× 3 |
|
= 10 + 27 + 51+135 + 72 + 252 |
= 547. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2.5. Векторное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
Определение 2.13. |
Векторным |
|
произведением |
векторов |
a |
|
и |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
называется |
|
|
|
|
|
|
|
|
|
вектор |
|
с, |
|
обозначаемый |
|
|
c = a ´ |
|
|
|
|
|
или |
c = [a, |
|
] |
|
и |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
удовлетворяющий следующим условиям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
× sin ϕ, , где j - угол между векторами a и |
|
, sinϕ ³ 0; 0 £ ϕ £ π ; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
c |
|
= |
|
a |
|
× |
|
|
|
|
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
b |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2)вектор с ортогонален векторам a и b;
3)векторы a , b и с образуют правую тройку векторов, т.е. для наблюдателя, находящегося в конце вектора с обход от вектора a к
вектору b совершается против часовой стрелки.
Основные свойства векторного произведения векторов сформулированы в следующей теореме.
Теорема 2.6. Справедливы следующие утверждения:
1. Векторное произведение векторов антикоммутативно:
b´ a = -a ´ b.
2.Векторное произведение векторов равно нулевому вектору в том и только в том случае, когда векторы коллинеарны или хотя бы один из них равен нулю:
a ´ b = 0 Û a ïïb, или a = 0, или b = 0.
40
PDF created with pdfFactory Pro trial version www.pdffactory.com
