
Линейная алгебра и аналитическая геомерия
.PDF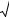
Из уравнений |
видно, что k1 = 2, k2 |
= -3. Подставляя |
|
эти значения в |
||||||
формулу (3.7), находим |
|
|
|
|
|
|
||||
|
|
tgϕ = |
-3 - 2 |
|
= -5 = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1- 3× 2 |
|
-5 |
|
|
|
|
|
|
Таким образом, угол между данными прямыми равен 45o. |
|
|
||||||||
Если прямые l1 |
и l2 параллельны, то ϕ = 0o и tgϕ = 0. |
Из формулы (3.7) |
||||||||
следует, что k2 - k1 = 0 , откуда l1 = l2 . |
|
|
|
|
|
|
||||
Если прямые l1 |
и l2 |
перпендикулярны, то ϕ = 90o , |
α2 = 90o +α1, |
|||||||
|
k2 |
= tgα2 = tg(α1 + 90o ) = -ctgα1 = - |
1 |
= - |
1 |
. |
||||
|
tgα1 |
|
||||||||
|
|
|
|
|
|
|
k1 |
|
|
|
Таким образом, верна следующая
Теорема 3.1. Справедливы утверждения
1.Две прямые на плоскости параллельны тогда и только тогда, когда их угловые коэффициенты равны.
2.Две прямые на плоскости перпендикулярны тогда и только тогда,
когда их угловые коэффициенты обратны по величине и противоположны по знаку.
Из теоремы 2.8, в частности, следует, что прямая, проходящая через точку Mo (xo , yo ) параллельно прямой y = kx + b, имеет уравнение
y - yo = k(x - xo ); |
(3.8) |
|
если же прямая проходит через точку |
Mo (xo , |
yo ) и перпендикулярна прямой |
y = kx + b, то она имеет уравнение |
|
|
y - yo = - 1 |
(x - xo ). |
(3.9) |
k |
|
|
В ряде геометрических задач необходимо знать координаты точки пересечения двух прямых. Аналитически их можно отыскать как решение системы двух линейных уравнений этих прямых.
3.1.1.7. Расстояние от точки до прямой |
|
|
|
|
|
|
|||
Определение 3.9. Расстоянием d = ρ(M o ,l) от точки |
M o |
до прямой |
l |
||||||
называется длина перпендикуляра, проведённого из точки |
M o к прямой l. |
|
|||||||
Теорема 3.2. Расстояние d = ρ(M o ,l) от |
точки Mo (xo , |
yo ) до прямой l |
с |
||||||
общим уравнением (3.1) вычисляется по формуле |
|
|
|
||||||
d = |
|
A× xo + B × yo |
+ C |
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
A2 + B2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
51
PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример. Даны вершины треугольника А(0, 1), B(6, 5), C(12, -1). Вычислить длину высоты, проведённой из вершины С.
Воспользуемся теоремой 3.2. Для этого составим уравнение стороны
АВ:
x - 0 = y -1, 6 - 0 5 -1
6x = y4-1,
общее уравнение прямой АВ имеет вид:
2x − 3y + 3 = 0.
Тогда
|
|
|
2×12 - 3×(-1) + 3 |
|
|
|
|
|
30 |
|
|
30 |
|
|
|||
d = ρ(C, AB) = |
|
|
|
|
= |
|
|
|
= |
13 |
» 8,32. |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|||||
22 + (-3)2 |
|
|
|
|
|
13 |
|
|
|||||||||
3.1.2. Кривые второго порядка
3.1.2.1. Определение кривой второго порядка. Классификация кривых второго порядка
Определение 3.10. Кривой второго порядка называется линия на плоскости, заданная уравнением
Ax2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0,
где A, B, C, D, E, F − действительные числа, причём A, и B и C не равны нулю одновременно, т.е. A2 + B2 + C2 ¹ 0.
Существует система координат (не обязательно прямоугольная декартова), в которой данное уравнение второго порядка может быть представлено в одном из видов, приведённых ниже, называемых
каноническим уравнением и соответствующих указанной кривой второго порядка (Таблица 1):
|
|
|
|
|
|
|
|
|
Таблица 1 |
|
|
|
Каноническое уравнение |
Название кривой |
|||||
|
|
|
кривой второго порядка |
второго порядка |
|||||
|
x2 |
+ |
|
y2 |
|
= 1 |
эллипс |
||
|
a2 |
|
b2 |
||||||
|
|
|
|
|
|
||||
(x - a)2 + (y - b)2 = R2 |
окружность |
||||||||
|
x2 |
|
+ |
y2 |
|
= -1 |
мнимый эллипс |
||
|
a2 |
|
b2 |
||||||
|
|
|
|
|
|
||||
|
x2 |
|
- |
y2 |
|
= 1 |
гипербола |
||
|
a2 |
|
|
||||||
|
|
|
|
b2 |
|
|
|||
|
y2 = 2 px |
|
парабола |
||||||
52
PDF created with pdfFactory Pro trial version www.pdffactory.com
a2 x2 - b2 y2 = 0 |
пара пересекающихся |
|
|
|
прямых |
y2 |
- a2 = 0 |
пара параллельных прямых |
y2 |
+ a2 = 0 |
пара мнимых параллельных |
|
|
прямых |
y2 |
= 0 |
пара совпадающих прямых |
Далее рассмотрим кривые второго порядка, наиболее часто встречающиеся при решении геометрических задач.
3.1.2.2. Окружность
Определение 3.11. Окружностью ω(C, R) с центром в точке C(a, b) и радиусом R называется кривая второго порядка, каноническое уравнение
которой имеет вид
(x - a)2 + (y - b)2 = R2 .
Пример. Найдём координаты центра и радиус окружности, если её уравнение задано в виде 2x2 + 2y2 - 8x + 5y - 4 = 0.
Для вычисления координат центра и радиуса окружности данное уравнение приведём к каноническому виду, указанному в определении
3.11.Для этого выделим полные квадраты:
x2 + y2 - 4x + 2,5y - 2 = 0,
(x2 - 2 × x × 2 + 22 ) - 22 + ( y2 + 2 × y × 5 / 4 + (5 / 4)2 ) - (5 / 4)2 = 0, (x - 2)2 + (y + 5/ 4)2 = 2 + 4 + 25/16,
(x - 2)2 + (y + 5/ 4)2 =121/16, (x - 2)2 + (y + 5/ 4)2 = (11/ 4)2 ,
отсюда находим окружностьω(C, R), у которой центрC(2, − 5 / 4) и радиус
R =11/ 4.
3.1.2.3. Эллипс
Определение 3.12. Эллипсом γ называется кривая второго порядка,
каноническое уравнение которой имеет вид |
|
||||
|
x2 |
+ |
y2 |
= 1. |
(3.10) |
|
a2 |
b2 |
|||
|
|
|
|
||
Определение 3.13. Фокусами эллипса называются такие две точки плоскости F1 и F2 , сумма расстояний от которых до любой точки М эллипса γ есть величина постоянная. При этом фокус F1 называется левым фокусом, а F2 - правым фокусом.
53
PDF created with pdfFactory Pro trial version www.pdffactory.com

Из определения 3.13 вытекает способ построения эллипса с помощью натянутой нити, показанный на рис. 16 и дающий представление о форме эллипса: это – замкнутая выпуклая линия с двумя осями симметрии (осями абсцисс и ординат), называемыми главными осями эллипса, и с центром симметрии O, называемым центром эллипса.
y
М
|
|
r1 |
r2 |
|
|
|
O |
|
|
|
F1 |
F2 |
x |
|
|
Рисунок 16. Эллипс |
|||
Обозначим расстояние F1F2 |
между фокусами эллипса, изображённого |
|||
на рис.16, через 2c. Тогда фокусы имеют координаты F1 (−c, 0) и F2 (c, 0). |
||||
Из определения 3.13 следует, что |
величина r1 + r2 постоянна. Для |
|||
эллипса с каноническим уравнением (3.10) эта величина равна 2a. |
||||
Очевидно, что 2a > 2c. |
Величина |
b2 , |
входящая в уравнение (3.10), |
|
определяется как разность |
|
b2 = a2 − c2. |
||
|
|
|||
Определение 3.14. Число a |
( 2a ) называется большой полуосью (большей |
|||
осью) эллипса γ с каноническим уравнением (3.10),а число b (2b) − его
малой полуосью (малой осью). |
|
Определение 3.15. Точки плоскости |
(−a, 0), (a, 0), (0, − b), (0, b) называются |
вершинами эллипса. При этом (−a, 0) |
и (a, 0) − соответственно левая и |
правая вершины эллипса, (0, − b) и (0, b) − соответственно нижняя и верхняя
вершины эллипса.
Определение 3.16. Числоε , равное отношению фокусного расстояния 2c к большей оси 2a, называется эксцентриситетом эллипса:
ε = 22aс .
Эксцентриситет эллипса – безразмерная величина, для вычисления которой применяется одна из формул:
|
|
|
|
|
|
ε = |
c |
= |
a2 − b2 . |
||
a |
|||||
|
|
a2 |
|||
Поскольку у эллипса 2a > 2c, его эксцентриситет ε < 1. Эксцентриситет эллипса говорит о его форме (степени вытянутости). При уменьшении ε фокусы эллипса F1 и F2 сближаются, а малая полуось приближается к большой. В пределе, когда ε = 0, т.е. фокусное расстояние равно нулю,
54
PDF created with pdfFactory Pro trial version www.pdffactory.com

эллипс вырождается в окружность. Следовательно, окружность является особым предельным случаем эллипса, если его фокусы совпали с центром. Если же эксцентриситет увеличивается, приближаясь к 1, то
эллипс становится всё более вытянутым и в пределе вырождается в отрезок.
Теорема 3.3. Если для некоторой точки Mo (xo , yo ) плоскости выполняется
условие
x2 |
|
y2 |
<1, |
|
o |
+ |
o |
||
a2 |
b2 |
|||
|
|
то точка M o находится внутри эллипса, а если
x2 |
|
y2 |
> 1, |
|
o |
+ |
o |
||
a2 |
b2 |
|||
|
|
то точка M o находится вне эллипса.
Теорема 3.4. Для произвольной точки Mo (xo , yo ) , принадлежащей эллипсу,
верны равенства:
r1 = a -ε × x, r2 = a + ε × x.
Определение 3.17. Пара прямых, заданных уравнениями
x = ± εa ,
называется директрисами эллипса с каноническим уравнением (3.10).
Теорема 3.5. Для принадлежности точки эллипсу необходимо и достаточно того, чтобы отношение расстояния от этой точки до фокуса к
расстоянию от неё до соответствующей директрисы было равно эксцентриситету.
Пример. Составим уравнение прямой, проходящей через левый фокус и
нижнюю вершину эллипса, заданного уравнением x2 + y2 = 1. 25 16
Большая полуось эллипса a = 5, его меньшая полуось b = 4. Координаты нижней вершины эллипса, в соответствии с определением
3.15, равны |
(0, − 4) . |
||
Так как |
b2 = a2 - c2 , получим c = |
|
= 3. Координаты левого фокуса |
25 -16 |
|||
эллипса F1(-3, 0)
Уравнение прямой, проходящей через две точки (0, − 4) и (−3, 0) имеет
вид:
55
PDF created with pdfFactory Pro trial version www.pdffactory.com
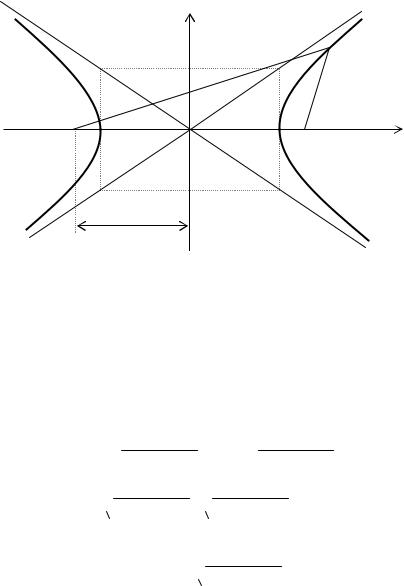
x − 0 |
= |
y + 4 |
, |
||||
− 3 − 0 |
|
|
|||||
0 + 4 |
|
||||||
|
x |
= |
y + 4 |
, |
|
||
|
|
|
|
||||
|
− 3 |
4 |
|
|
|||
4x = −3y −12,
4x + 3y +12 = 0.
3.1.2.4. Гипербола
Определение 3.18. Гиперболой называется множество точек M плоскости, модуль разности расстояний от которых до двух данных точек F1 и F2 , называемых фокусами, есть величина постоянная, меньшая
расстояния между ними (рис. 17)
|
y |
|
|
b |
M |
|
|
r1 |
|
|
r2 |
|
O |
x |
F1 |
a F2 |
c
Рисунок 17. Гипербола
Обозначим расстояние F1F2 между фокусами гиперболы, изображённой на рис.17, через 2c. Тогда фокусы имеют координаты F1 (−c, 0) и F2 (c, 0).
Из определения 3.18 следует, что величина | r1 + r2 | постоянна.
Обозначим её через 2a. Выберем на гиперболе произвольную точку M (x, y).. Тогда из геометрических соображений, приведённых на рисунке
3.18, следуют равенства
r1 = 
 (x + c)2 + y2 и r2 =
(x + c)2 + y2 и r2 = 
 (x − c)2 + y2 ,
(x − c)2 + y2 ,
откуда получим уравнение

 (x + c)2 + y2 −
(x + c)2 + y2 − 
 (x − c)2 + y2 = 2a.
(x − c)2 + y2 = 2a.
Уединяя первый радикал в левой части и возводя полученное уравнение в квадрат, получим
(x + c)2 + y2 = 4a2 + 4a
 (x − c)2 + y2 + (x − c)2 + y2 ,
(x − c)2 + y2 + (x − c)2 + y2 ,
56
PDF created with pdfFactory Pro trial version www.pdffactory.com

4a
 (x − c)2 + y2 = −4a2 + 4xc.
(x − c)2 + y2 = −4a2 + 4xc.
Возведём последнее уравнение в квадрат, получим: a2 (x − c)2 + a2 y2 = a4 − 2a2 xc + x2c2 ,
a2 x2 − 2a2 xc + a2c2 + a2 y2 = a4 − 2a2 xc + x2c2 , a2 x2 + a2c2 + a2 y2 − a4 − x2c2 = 0,
−x2 (c2 − a2 ) + a2 (c2 − a2 ) + a2 y2 = 0,
x2 (c2 − a2 ) − a2 y2 = a2 (c2 − a2 ).
Обозначим c2 − a2 = b2.Тогда уравнение примет вид a2b2 = b2 x2 − a2 y2
или |
|
|
|
|
|
|
x2 |
− |
y2 |
=1. |
(3.11) |
|
a2 |
b2 |
|||
|
|
|
|
||
Определение 3.19. Уравнение (3.11) называется каноническим уравнением гиперболы. Число a ( 2a ) называется действительной полуосью (действительной осью) гиперболы с каноническим уравнением (3.11),а число b (2b) − его мнимой полуосью (мнимой осью).
Гипербола пересекает действительную ось в двух точках (−a, 0) и (a, 0) − соответственно в левой и правой вершинах. Мнимую ось гипербола
не пересекает. Из рисунка 17, равно как и из уравнения 3.11, видно, что гипербола имеет две оси симметрии (оси абсцисс и ординат), называемые её главными осями, а также центр симметрии (точка O), называемый её центром. Для гиперболы, в отличие от эллипса, справедливо неравенство
2a < 2c.
Определение 3.20. Пара прямых, заданных уравнениями y = ± ba x,
называется асимптотами гиперболы с каноническим уравнением (3.11). Определение 3.21. Числоε , равное отношению фокусного расстояния 2c к действительной оси 2a, называется эксцентриситетом гиперболы:
ε = 22aс .
Эксцентриситет гиперболы – безразмерная величина, для вычисления которой применяется одна из формул:
|
|
|
|
|
|
ε = |
c |
= |
a2 + b2 . |
||
a |
|||||
|
|
a2 |
|||
Поскольку у гиперболы 2a< 2c, её эксцентриситет ε > 1.
Определение 3.22. Если у гиперболы действительная и мнимая оси равны, т.е. a = b, то гипербола называется равнобочной (равносторонней).
Очевидно, что эксцентриситет равнобочной гиперболы ε = 
 2. Определение 3.23. Пара прямых, заданных уравнениями
2. Определение 3.23. Пара прямых, заданных уравнениями
57
PDF created with pdfFactory Pro trial version www.pdffactory.com

x = ± εa ,
называется директрисами гиперболы с каноническим уравнением (3.11).
Директрисы гиперболы перпендикулярны её действительной оси и расположенны симметрично относительно центра гиперболы на
расстоянии εa от него.
Теорема 3.6. Если r – расстояние от произвольной точки М гиперболы до какого-либо фокуса, d – расстояние от той же точки до соответствующей
этому фокусу директрисы, то отношение dr – величина постоянная, равная эксцентриситету гиперболы ε.
Пример. Составим уравнение гиперболы, если её эксцентриситет ε = 2, а
фокусы совпадают с фокусами эллипса |
x2 |
+ |
y2 |
= 1. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
25 |
9 |
|
|
|
|
|
||||
Для эллипса c2 = a2 − b2 = 25 − 9 = 16, |
т.е. |
его фокусы имеют координаты |
|||||||||||
F1 (−4, 0) и F2 (4, 0). |
|
|
|
|
|
|
|
|
|
|
|
||
Для гиперболы c2 = a2 + b2 =16, ε = |
c |
|
= |
4 |
= 2, откуда |
|
|
|
|||||
a |
|
|
|
|
|||||||||
|
|
a |
|
|
|
|
|
|
|
||||
|
a = 2, |
|
|
|
|
|
|
|
|||||
b2 = c2 − a2 = 16 − 4 = 12 . |
|
|
|
|
|||||||||
Следовательно, уравнение гиперболы имеет вид |
x2 |
− |
y2 |
= 1. |
|||||||||
4 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
12 |
|
||
3.1.2.5. Парабола
Определение 3.24. Параболой называется множество точек М плоскости,
каждая из которых находится на одинаковом расстоянии от данной точки F, называемой фокусом, и от данной прямой d, называемой директрисой
и не проходящей через фокус.
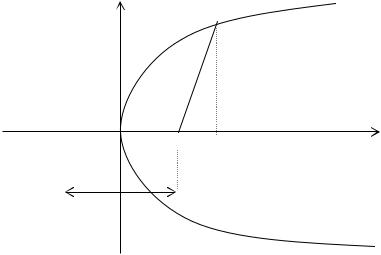
Каноническое уравнение параболы, расположенной в прямоугольной декартовой системе координат в соответствии с рис. 18, имеет вид:
y2 = 2 px. |
(3.12) |
Величина p (расстояние от фокуса F |
до директрисы d ) называется |
параметром параболы. Фокус параболы с каноническим уравнением (3.12)
имеет координаты
F( p / 2, 0),
ауравнение директрисы этой параболы имеет уравнение
x= 2p .
58
PDF created with pdfFactory Pro trial version www.pdffactory.com
|
|
|
|
y |
|
|||
|
|
|
|
|
||||
|
|
|
|
|
|
М |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
F |
x |
|
|
|
p |
|
|
p |
|
|
|
|
2 |
|
2 |
|
|
|
||
|
|
Рисунок 18. Парабола |
||||||
|
|
|||||||
Пример. На параболе y2 = 8x |
|
найдём точку, |
расстояние от которой до |
|||||
директрисы равно 4.
Из канонического уравнения параболы (3.12) получаем значение
параметра |
p = 4. Очевидно, расстояние от точки на |
параболе |
до её |
||||
директрисы равно x + |
p |
, откуда абсцисса искомой точки |
x = 4 - |
p |
= 2. |
Тогда |
|
|
2 |
||||||
|
2 |
|
|
|
|
||
y2 = 8×2 =16, |
т.е. ордината искомой точки y = ±4. |
|
|
|
|
||
M1 (2,4) |
и M 2 (2, - 4) - искомые точки параболы. |
|
|
|
|
||
3.1.3.Уравнение линии в полярных координатах
Влюбой системе координат на плоскости, в том числе и в полярной, уравнение между этими координатами (за исключением особых случаев, которые мы рассматривать не будем) определяет некоторую линию. Будем считать, что уравнение разрешено относительно полярного радиуса ρ, т.е. имеет вид
ρ= f (ϕ).
Придавая полярному углу ϕ конкретные числовые значения и находя соответствующее значение ρ, получим точки, которые образуют линию на
плоскости – график функции в полярных координатах.
Ниже рассмотрим пример, связанный с кривыми второго порядка в полярных координатах.
59
PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример. Уравнение кривой в полярной системе координат имеет вид
ρ = |
4 |
Составим уравнение этой кривой в прямоугольной декартовой |
3 - cosϕ . |
системе координат и определим её тип и основные характеристики.
Воспользуемся связью прямоугольной декартовой и полярной систем координат, рассмотренной нами в пункте 2.2.2:
ρ = |
|
, |
cosϕ = |
|
|
x |
|
|
|
x2 + y2 |
|
. |
|||||||
|
|
|
|
||||||
x2 |
+ y2 |
||||||||
|
|
|
|
|
|
|
Тогда уравнение примет вид:
|
|
|
|
|
|
|
4 |
|
|
|
||||
|
x2 + y2 = |
|
|
|
|
|
, |
|||||||
|
|
|
|
|
|
|
|
x |
||||||
|
|
3 - |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
x2 + y2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
3 |
|
x2 + y2 |
|
- x = 4, |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
3 |
|
x2 + y2 |
|
= x + 4, |
|
|||||||||
9x2 + 9y2 = 16 + 8x + x2 , |
|
|||||||||||||
8x2 - 8x + 9y2 -16 = 0, |
|
|||||||||||||
8(x2 - x +1/ 4) - 8×1/ 4 + 9y2 -16 = 0, |
||||||||||||||
8(x -1/ 2)2 - 2 + 9y2 -16 = 0, |
||||||||||||||
|
8(x -1/ 2)2 + 9y2 |
=18, |
|
|
||||||||||
|
(x -1/ 2)2 |
+ |
|
y2 |
|
=1. |
|
|
||||||
|
|
9/ 4 |
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||
Получили уравнение эллипса. Из уравнения видно, что центр эллипса
сдвинут вдоль оси абсцисс на 1/ 2 единиц вправо, |
большая полуось a = 3/ 2, |
|||||||
меньшая полуось b = |
|
|
||||||
2, половина расстояния между фокусами равно с = |
||||||||
|
|
|
Эксцентриситет |
эллипса равен |
ε = c / a = 1/ 3, |
фокусы |
||
c = a2 - b2 =1/ 2. |
||||||||
расположены в точках F1 (0, 0) и F1 (1, 0). |
|
|
||||||
3.2. Поверхности и линии в пространстве |
|
|
||||||
Определение |
3.25. |
|
Любое |
уравнение F(x, y, z) = 0, связывающее |
||||
прямоугольные декартовы координаты x, y, z любой точки поверхности,
называется уравнением этой поверхности в прямоугольной декартовой системе координат.
Если первоначально дана некоторая поверхность в пространстве, то, формулируя аналитически свойство, определяющее эту поверхность, можно получить уравнение этой поверхности. При этом следует учитывать, что каждое уравнение можно переписать в различных эквивалентных формах. Это даёт возможность взамен поверхностей
рассматривать их уравнения и тем самым сводить геометрические задачи к алгебраическим. Например, для того чтобы проверить, проходит
60
PDF created with pdfFactory Pro trial version www.pdffactory.com
