
Линейная алгебра и аналитическая геомерия
.PDF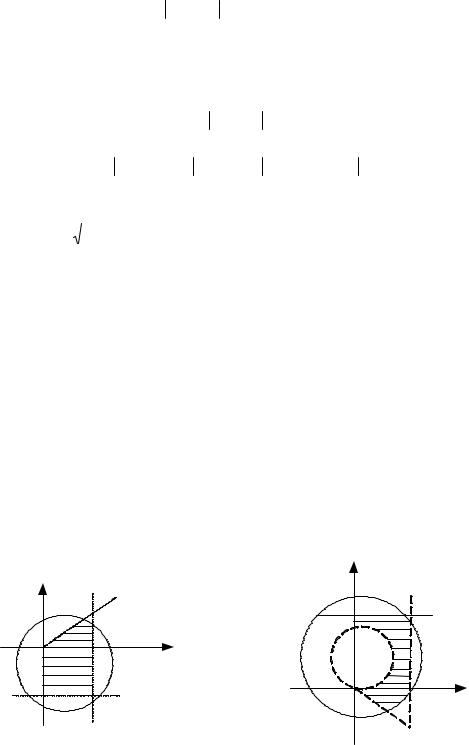
ì z -1+ 2i £ 4, |
|
|
|||
ï |
|
|
|
|
|
ïRe z < 3, |
|
|
|
||
ï |
|
|
|
|
|
íIm z < -3, |
|
|
|
||
ï |
π |
|
|
π |
|
ï |
£ arg z |
< |
. |
||
ï- |
2 |
4 |
|||
î |
|
|
|
||
Рассмотрим неравенство z -1+ 2i £ 4. Положим z = x + iy, тогда
неравенство примет вид
x + iy -1+ 2i £ 4 или (x -1) + (y + 2)i £ 4.
Пользуясь определением модуля комплексного числа, запишем
неравенство в виде
|
|
|
|
|
|
|
|
|
|
|
(x |
-1) |
2 + ( y + 2)2 £ 4 или (x -1)2 + (y + 2)2 £ 42 , |
||
т.е. неравенство |
|
z -1 |
+ 2i |
|
£ 4 задаёт множество точек, лежащих внутри круга |
||
|
|
||||||
и на окружности радиуса 4 с центром в точке A(1, − 2) .
Рассмотрим неравенство Re z < 3. Положим z = x + iy, тогда неравенство
примет вид |
x < 3, |
т.е. неравенство Re z < 3 |
определяет множество точек, |
|||
лежащих левее вертикальной прямой x = 3. |
|
|
||||
Аналогично неравенство |
Im z < −3 задаёт множество точек, |
лежащих |
||||
выше горизонтальной прямой y = −3. |
|
|
||||
Неравенство |
- π |
£ arg z < π |
задаёт множество точек, принадлежащих |
|||
|
|
2 |
4 |
|
|
|
углу между |
лучами |
arg z = - π |
и arg z = π , |
причём точки луча |
arg z = - π |
|
|
|
|
2 |
4 |
|
2 |
принадлежат углу, а точки луча arg z = π4 ему не принадлежат.
Искомое множество получается пересечением указанных выше множеств (рис. 33а).
|
|
y |
y |
|
|
O |
x |
j |
|
0 |
x |
Рисунок 33а |
Рисунок 33б |
Пример. Построить множество точек удовлетворяющих системе нера-
венств
91
PDF created with pdfFactory Pro trial version www.pdffactory.com

ì1 < z - i £ 3, |
|
|
||
ï |
|
|
|
|
ïIm z £ 3, |
|
|
||
ï |
|
|
|
|
íRe z < 2, |
|
|
||
ï |
π |
|
π |
|
ï |
< arg z £ |
. |
||
ï- |
4 |
2 |
||
î |
|
|
||
Неравенство |
1 < |
|
z - i |
|
£ 3 |
задаёт кольцо с центром в точке |
A(0, 1), |
|||||
|
|
|||||||||||
ограниченное окружностями с радиусами R = 1 и R = 3. Точки окружности с с |
||||||||||||
центром в точке |
A(0, 1) и радиусом |
R = 1 кольцу не принадлежат, |
а точки |
|||||||||
окружности с центром в точке A(0, 1) |
и радиусом R = 3 принадлежат кольцу. |
|||||||||||
Неравенства |
Im z ≤ 3 и |
Re z < 2 |
определяют полуплоскости, |
лежащие |
||||||||
ниже и на прямой Im z = 3 и левее прямой Re z = 2 соответственно. |
|
|
||||||||||
Неравенство |
- π < arg z £ |
π |
определяет угол между лучами |
arg z = - π , |
||||||||
|
π , |
|
4 |
|
|
|
|
2 |
|
|
|
4 |
arg z = |
причём точки луча |
arg z = - |
π не принадлежат углу, а точки луча |
|||||||||
|
2 |
|
|
|
|
|
|
|
|
4 |
|
|
arg z = |
π |
ему принадлежат. |
|
|
|
|
|
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Искомое множество изображено на рис. 33б.
4.3. Тригонометрическая и показательная формы комплексного числа
Из рис. 32 следуют формулы:
a =| z | cosϕ, b =| z | sinϕ,
подставляя которые в равенство (4.1), получаем то же комплексное число z, записанное в тригонометрической форме:
z =| z |(cosϕ + isinϕ).
Применяя к последнему равенству формулу Эйлера cosϕ + i sinϕ = ei ϕ ,
приходим к показательной форме комплексного числа z :
z=| z |eiϕ .
Втригонометрической и показательной формах операции умножения и деления комплексных чисел можно определить следующим образом.
Определение 4.9. Произведением двух комплексных чисел
z1 =| z1 | (cosϕ1 + i sinϕ1 ) |
и z2 =| z2 | (cosϕ2 + isinϕ2 ) |
называется комплексное число z3 , |
|||||
обозначаемое z1 × z2 , такое, что |
|
|
|
|
|
||
|
z = z1 × z2 =| z1 | × | z2 | (cos(ϕ1 + ϕ2 ) + isin(ϕ1 +ϕ2 )). |
||||||
Определение 4.10. |
Частным от |
деления |
|
|
комплексного числа |
||
z1 =| z1 | (cosϕ1 + i sinϕ1 ) |
на |
комплексное |
число |
z1 |
|
z2 =| z2 | (cosϕ2 + i sinϕ2 ) ¹ 0 |
|
называется комплексное число z3 , обозначаемое |
|
, |
такое, что |
||||
|
z2 |
||||||
|
|
|
|
|
|
|
|
92
PDF created with pdfFactory Pro trial version www.pdffactory.com

z = |
z1 |
= |
| z1 |
| |
(cos(ϕ -ϕ |
2 |
) + isin(ϕ -ϕ |
2 |
)). |
|
|
|
|||||||
|
z2 |
|
| z2 |
| |
1 |
1 |
|
||
|
|
|
|
|
|
|
Из определения 4.9 следует формула возведения комплексного числа
в целую положительную степень
zn =| z |n (cosnϕ + i sin nϕ),
которая называется формулой Муавра.
Пример. Представим в тригонометрической и показательной формах ком-
плексные числа z1 = 3, |
z2 |
= -i, |
z3 = - |
|
|
|
3 |
- i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Для числа z1 = 3 действительная и мнимая части соответственно равны |
|||||||||||||||||||||||||||||||||||||||||
Re z = 3, |
Im z = 0. |
Тогда | z1 |= |
|
|
|
|
|
|
|
Точка A(3,0) |
|
лежит на действительной |
|||||||||||||||||||||||||||||
32 + 02 |
= 3. |
||||||||||||||||||||||||||||||||||||||||
оси, поэтому arg z1 = 0. |
Таким образом, тригонометрическая форма числа |
||||||||||||||||||||||||||||||||||||||||
имеет вид z1 = 3(cos0 + i sin 0), а показательная форма – z1 = 3ei×0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Число z2 = -i является чисто мнимым. |
|
|
|
|
|
|
|
|
Точка A(0, −1) |
||||||||||||||||||||||||||||||||
| z2 |= |
02 + (-1)2 |
|
= 1. |
||||||||||||||||||||||||||||||||||||||
лежит |
на |
мнимой |
|
оси, |
|
|
поэтому |
argz = - |
π . |
Таким |
|
образом, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
π |
|
|
|
|
|
π öö |
||
тригонометрическая форма |
числа |
имеет |
вид |
|
z2 |
æ |
æ |
- |
ö |
æ |
- |
||||||||||||||||||||||||||||||
|
= 1çcosç |
2 |
÷ + i sinç |
|
÷÷, а |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
è |
|
|
ø |
è |
|
|
|
2 øø |
||||
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
показательная форма – |
z2 = 1e-i 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для числа z3 = - |
|
- i |
модуль |
|
z3 |
|
|
= |
|
|
(- |
|
)2 + (-1)2 |
|
= 2. Точка A(- |
|
|
|
|
лежит |
|||||||||||||||||||||
3 |
3 |
3, -1) |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
-1 |
|
- π = arctg |
|
|
|
- π = - |
5 π . Таким образом, |
||||||||||||||||||||||||||||||
в III квадранте, поэтому arg z3 |
= arctg |
|
|
|
3 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
- |
3 |
|
|
|
3 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
æ |
|
|
5 |
|
ö |
æ 5 |
öö |
|||||
тригонометрическая форма числа имеет вид |
z3 = 2çcosç- |
|
|
π ÷ + i sinç |
|
|
π ÷÷, а |
||||||||||||||||||||||||||||||||||
6 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
è |
|
|
|
ø |
è 6 |
øø |
||||||
-5π i
показательная форма – z3 = 2e 6 . Пример. Вычислим (-1+ i
 3)5 .
3)5 .
Пусть -1+ i 3 = z . Найдем модуль и аргумент этого числа:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
z |
= |
(-1)2 + (+ |
|
3) = 2, |
|
|
arg z = arctgç |
- |
|
|
|
÷ |
+ π = - |
π + π = |
π. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
1 |
÷ |
|
3 |
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|||||||||
Тогда в тригонометрической форме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z = |
2çcos |
|
π + i sin |
|
|
|
π ÷. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|||
Применяя формулу zn =| z |n |
(cosnϕ + i sin nϕ) |
|
при n = 5, |
получим: |
|||||||||||||||||||||||||||||||
|
|
5 |
|
5 æ |
2 |
|
|
|
|
|
|
2 |
ö |
|
|
|
æ |
æ |
|
|
|
|
|
|
|
π |
ö |
æ |
|
π öö |
|||||
z |
|
= 2 |
çcos5× |
|
π + i sin 5 |
× |
|
π ÷ |
= 32çcosç |
3π + |
|
|
÷ + i sinç3π + |
÷÷ = |
|||||||||||||||||||||
|
3 |
3 |
3 |
||||||||||||||||||||||||||||||||
|
|
|
|
è |
|
|
|
|
|
|
ø |
|
|
|
è |
è |
|
|
|
|
|
|
|
ø |
è |
|
3 øø |
||||||||
|
|
|
|
|
|
π |
|
|
|
π |
|
|
|
|
æ |
|
|
|
|
|
|
|
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
ö |
|
|
1 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
- isin |
|
|
ç |
|
|
j |
÷ |
|
|
|
|
|
|
3i. |
|
|
|
|||||||||||||
|
|
|
= |
32ç- cos |
|
|
÷ = -32 |
|
+ |
|
|
|
÷ |
= -16 -16 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
è |
|
3 |
|
|
|
3 ø |
|
|
ç |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
93
PDF created with pdfFactory Pro trial version www.pdffactory.com

4.4. Извлечение корня натуральной степени из комплексного числа Определение 4.11. Комплексное число w называется корнем натуральной
степени n из комплексного числа |
z (w = n |
|
), если wn = z. |
z |
|||
Запишем комплексное число z |
в тригонометрической форме |
||
z =| z |(cosϕ + isinϕ).
Число w = n |
z |
будем искать в виде: |
|
|
|
||||||||
|
|
|
|
|
|
|
w =| w | (cosψ + isinψ ). |
|
|||||
Поскольку wn = z, |
то получим |
|
|
|
|
|
|
||||||
|
|
|
z =| z |(cosϕ + isinϕ) =| w |n (cosψ + i sinψ ), |
||||||||||
откуда | w |n =| z |, |
nψ = ϕ + 2πk, т.е. |
|
|
, ψ = ϕ + 2πk . |
|
||||||||
|
|
|
|
|
|
| w |= n |
|
|
|||||
|
|
|
| z | |
|
|||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
n |
|
||
|
|
|
|
|
ϕ + 2πk |
|
ϕ + 2πk ö |
|
|||||
|
|
|
|
|
|
|
æ |
+ isin |
(4.2) |
||||
|
|
|
|
|
|||||||||
|
|
|
n z = n | z |çcos |
|
n |
÷. |
|||||||
|
|
|
è |
|
|
n ø |
|
||||||
Уравнение |
|
wn = z |
|
имеет n |
различных корней. |
Все эти корни можно |
|||||||
найти, если в формуле (4.2) параметру k придать поочерёдно значения 0, 1, 2,K, n −1.
Пример. Найдём |
i |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модуль и аргумент комплексного числа z = i |
|
|
соответственно равны: |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
| i |= 1, |
argi = |
π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда тригонометрическая форма этого числа имеет вид: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
æ |
|
|
π |
+ i sin |
π |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
i =1×çcos |
2 |
2 |
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Применяя формулу (4.2), запишем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
æ |
|
π |
+ 2πk |
|
|
|
|
|
π |
|
|
+ 2πk |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ç |
|
2 |
|
|
|
|
|
2 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
i |
= |
1 |
çcos |
|
|
+ i sin |
|
|
|
|
|
|
÷, |
k = 0,1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
π |
+ i sin π |
= |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
||||||||||||||||||||
При k = 0 получим первое значение корня |
|
|
|
|
|
= cos |
2 |
|
+ i |
|
2 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
i |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
При k =1 получим второе значение корня |
|
|
|
|
= cos |
5 |
π + i sin |
5 |
π = - |
|
2 |
- i |
|
|
2 |
|
. |
||||||||||||||||||||||||||
|
|
i |
|||||||||||||||||||||||||||||||||||||||||
|
|
4 |
|
2 |
|
|
2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
94
PDF created with pdfFactory Pro trial version www.pdffactory.com
4.5.Разложение многочлена на множители. Основная теорема алгебры
Рассмотрим целую рациональную функцию от z = x + iy, т.е. многочлен
P(z) = a |
o |
zn + a zn−1 |
+ ...+ a |
n−1 |
z + a |
n |
, |
(4.3) |
|
1 |
|
|
|
|
степени n с, вообще говоря, комплексными коэффициентами an , an−1, ...,a0 ,
a0 ¹ 0.
Определение 4.13. Уравнение вида
P(z) = 0
называется алгебраическим уравнением степени n.
В элементарной алгебре доказывается следующая теорема, имеющая название теоремы Безу.
Теорема 4.3. Остаток от деления многочлена (4.3) на линейный двучлен z − c, где c ÎC, равен P(c).
Из теоремы Безу непосредственно вытекает справедливость следующего утверждения.
Следствие 4.1. Если z = c − корень многочлена (4.3), то этот многочлен делится на линейный двучлен z − c без остатка.
Следующая теорема носит название основной теоремы алгебры. Теорема 4.4. Любая целая рациональная функция P(z) вида (4.3), где n ³ 1,
имеет, по крайней мере, один комплексный корень (действительный или мнимый).
Если обозначить через z1 какой-либо из корней P(z), то, по следствию
4.1, P(z) нацело делится на двучлен z - z1 , т.е. P(z) = (z - z1 )P1 (z), где P1(z) - уже многочлен (n -1) - ой степени. Если к нему опять применить те же
рассуждения, то мы получим P1(z) = (z - z2 )P2 (z), т.е. P(z) = (z - z1 )(z - z2 )P2 (z), где P2 (z) - многочлен (n - 2) - ой степени. Эти рассуждения можно продолжать,
пока мы не дойдём до многочлена нулевой степени, т.е. постоянной.
Отсюда следует
Теорема 4.5. Любой многочлен n − ой степени P(z) представим в виде произведения n линейных множителей вида z − a и множитель a0 , равный коэффициенту при zn :
P(z) = ao (z - z1 )(z - z2 )K(z - zn ).
Из теоремы 4.5 следует, что все числа z1, z2 ,K, zn являются корнями многочлена P(z) и никаких других корней этот многочлен не имеет, т.е.
верна
Теорема 4.6. Алгебраическое уравнение степени n имеет ровно n корней.
95
PDF created with pdfFactory Pro trial version www.pdffactory.com

Некоторые из корней алгебраического уравнения могут совпадать друг с другом, повторяться; такие корни называются кратными (двойными, т.е. кратности 2, тройными, т.е. кратности 3, и т.д.) в отличие от простых, т.е. не повторяющихся корней. Поэтому при подсчёте числа корней каждый из них должен браться со своей кратностью. Так, если z1, z2 ,K, zk - различные
корни алгебраического уравнения |
P(z) = 0 |
и |
α1 , α2 ,K, αk - |
их |
соответствующие кратности, то в соответствии с теоремой 4.5, |
(4.4) |
|||
P(z) = ao (z - z1 )α1 (z - z2 )α2 K(z - zk )αk . |
|
|||
Теорема 4.7. Если многочлен (4.3) имеет только действительные коэффициенты, то он всегда вместе с мнимым корнем zi обладает
сопряжённым корнем zi , причём той же кратности αi .
Если в разложении (4.4) объединить множители, отвечающие комплексно-сопряжённым корням, то получим
[z - (a + ib)]×[z - (a - ib)] = (z - a)2 + b2 = z2 + pz + q,
где p = -2a, q = a2 + b2 . Такое объединение применяется при разложении
многочлена с действительными коэффициентами от действительного аргумента, который естественно обозначать через x. Тогда из (4.4)
получаем
P(x) = ao (x - x1 )α1 K(x - xr )αr (x2 + p1 x + q1 )β1 K(x2 + ps x + qs )βs , |
(4.5) |
где первые r скобок соответствуют действительным корням, а последние s − парам комплексно-сопряжённых мнимых корней. Поскольку числа p и q действительны, верна следующая
Теорема 4.8. Любой многочлен с действительными коэффициентами от действительного аргумента можно разложить на действительные линейные и квадратичные множители.
В том случае, если все корни действительные, то в разложении (4.5) присутствуют только линейные множители, а если все корни мнимые, то присутствуют только квадратичные множители. Показатели степеней α1 , K , αr , β1 , K , βs равны кратностям соответствующих корней; в частности,
для простых корней они равны единице.
Пример. Разложим многочлен P(z) = z2 + z +1+ i на линейные множители: z2 + z +1+ i = (z2 +1) + (z + i) = (z - i)(z + i) + (z + i) = (z + i)(z - i +1).
Пример. Многочлен P(z) с действительными коэффициентами имеет простой корень z =1, двукратный корень z = i и простой корень z =1+ i. Найдём P(z), если известно, что P(−1) = 1.
96
PDF created with pdfFactory Pro trial version www.pdffactory.com
Число i является двукратным корнем алгебраического уравнения P(z) = 0, поэтому комплексно-сопряжённое число i = -i также является его
двукратным корнем. Число 1+ i − простой корень алгебраического уравнения P(z) = 0, следовательно, комплексно-сопряжённое число 1+ i = 1- i является простым корнем уравнения.
Таким образом, с учётом кратности, многочлен P(z) с действительными коэффициентами имеет 7 корней и представим в виде
P(z) = a0 (z -1)(z - i)2 (z + i)2 (z -1- i)(z -1+ i).
Коэффициент a0 определим из условия P(−1) = 1:
a0 (-1-1)(-1- i)2 (-1+ i)2 (-1-1- i)(-1-1+ i) = 1, a0 (-2)((1+ i)(1- i))2 (-2 - i)(-2 + i) =1,
a0 (-2)(12 - i2 )2 ((-2)2 - i2 ) = 1, a0 (-2) × 4×5 = 1,
a0 = - 401 (-2).
Тогда
P(z) = - 401 (z -1)(z - i)2 (z + i)2 (z -1- i)(z -1+ i) =
=- 401 (z -1)(z2 - i2 )2 (z2 - z + iz - z +1- i - iz + i - i2 ) =
=- 401 (z -1)(z2 +1)2 (z2 - 2z + 2) =
=- 401 (z -1)(z4 + 2z2 +1)(z2 - 2z + 2) =
=- 401 (z5 - z4 + 2z3 - 2z2 + z -1)(z2 - 2z + 2) =
= − 401 z7 + 403 z6 − 203 z5 + 15 z4 − 409 z3 + 18 z2 − 101 z + 201 .
Пример. Если в условиях предыдущего примера убрать требование на принадлежность коэффициентов многочлена P(z) множеству действительных чисел, то, очевидно, P(z) будет многочленом четвёртой степени, причём
P(z) = a0 (z -1)(z - i)2 (z -1- i).
Тогда
a0 (-1-1)(-1- i)2 (-1-1- i) = 1, a0 (-2)(1+ 2i + (-i)2 )(-2 - i) = 1, a0 (-2) × 2i ×(-2 - i) = 1,
a0 (-4) ×(-2i - i2 ) = 1, a0 (-4) ×(-2i +1) = 1,
97
PDF created with pdfFactory Pro trial version www.pdffactory.com

a |
0 |
= |
|
1 |
|
|
= |
|
|
|
|
- 4 - 8i |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
- 4 - 8i |
|
|
|
|
|
= |
|
- 4 - 8i = |
- 4 - 8i |
= - |
|
1 |
+ |
|
|
1 |
i. |
||||||||||||||||||||||||||||||||||
- 4 + 8i |
|
(-4 + 8i)(-4 - 8i) |
|
|
(-4)2 - (8i)2 |
|
|
|
20 |
10 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 + 64 |
|
|
|
80 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
ö |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
P(z) = ç- |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
i ÷(z -1)(z |
|
|
- |
|
2iz + i |
|
)(z -1- i), |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
ö |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P(z) = ç |
- |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
i÷(z -1)(z |
|
|
- 2iz -1)(z -1- i), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
ö |
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
P(z) = |
ç- |
|
|
|
|
|
+ |
|
|
|
|
|
i |
÷(z |
|
|
|
- 2iz |
|
|
- z |
- z |
|
|
|
+ 2iz +1)(z -1- i), |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
20 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
æ |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
ö |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
P(z) = |
ç |
- |
|
|
|
+ |
|
|
|
|
i÷(z |
|
|
|
+ (-2 - 3i)z |
|
+ (1 |
+ 3i)z |
|
|
+ (4 |
- i)z + (-1- i)), |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
20 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
æ |
|
|
1 |
|
|
|
|
1 |
ö |
|
|
4 |
|
|
æ |
2 |
|
|
|
|
1 |
|
|
|
|
|
ö |
|
|
|
3 |
æ |
|
|
7 |
|
|
|
|
|
1 |
|
|
|
ö |
2 |
æ |
1 |
|
9 |
|
ö |
|
3 |
|
|
|
|
1 |
|
|||||||||||||||||
P(z) = ç |
- |
|
|
|
+ |
|
|
|
|
i ÷z |
|
+ ç |
|
|
|
|
|
- |
|
|
|
|
|
|
i ÷z |
|
+ ç- |
|
|
|
|
|
- |
|
|
|
|
|
|
i÷z |
|
|
+ ç- |
|
|
|
+ |
|
i ÷z + |
|
|
|
- |
|
|
|
i. |
|||||||||||||||||||||||
20 |
|
10 |
|
5 |
|
20 |
|
20 |
|
20 |
|
|
|
10 |
20 |
20 |
20 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
è |
|
|
|
ø |
|
|
|
|
|
è |
|
|
|
|
|
|
|
ø |
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
è |
|
|
ø |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Пример. Решим квадратное уравнение x2 +14x + 53 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дискриминант |
|
|
|
|
|
квадратного |
|
|
|
|
уравнения |
|
|
|
|
D = 142 - 4×1×53 = -16 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отрицательный, следовательно, уравнение не имеет действительных корней, но имеет пару комплексно-сопряжённых корней:
x1 = -142-×1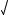 D = -14 -2
D = -14 -2
 -16 = -142- 4i = -7 - 2i, x2 = -142+×1
-16 = -142- 4i = -7 - 2i, x2 = -142+×1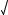 D = -14 +2
D = -14 +2
 -16 = -142+ 4i = -7 + 2i.
-16 = -142+ 4i = -7 + 2i.
4.6.Разложение дробно-рациональной функции на простейшие рациональные дроби
Определение 4.14. Функция f (x) = QP((xx)) , равная отношению многочлена
Q(x) = bo xm + b1xm−1 + ...+ bm−1x + bm
к многочлену
P(x) = ao xn + a1 xn−1 + ...+ an−1 x + an ,
называется дробно-рациональной функцией. При этом если m < n, дробь
Q(x) называется правильной, в других случаях – неправильной.
P(x)
Если дробь неправильная, то её всегда можно представить в виде суммы целой части (многочлена) и правильной дроби. Это можно сделать,
кпримеру, путём деления числителя дроби на её знаменатель столбиком.
Вотличие от числовых дробей сумма правильных дробно- рациональных функций также является правильной дробью.
Среди дробно-рациональных функций особо выделяют класс элементарных дробей.
Определение 4.15. Дробно рациональные функции вида
A |
, |
B |
, |
Cx + D |
и |
Ex + F |
, |
|
ax + b |
(ax + b)l |
ax2 + bx + c |
(ax2 + bx + c)l |
|||||
|
|
|
|
98
PDF created with pdfFactory Pro trial version www.pdffactory.com
где A, B, C, D, E, F, a, b, c - действительные числа, l ³ 2- натуральное число, b2 − 4ac < 0, называются элементарными дробями соответственно первого, второго, третьего и четвёртого типов.
Теорема 4.8. |
Если f (x) = |
Q(x) |
− правильная рациональная дробь, |
|
P(x) |
||||
|
|
|
||
знаменатель P(x) |
которой представлен в виде (4.5), то эта дробь может |
|||
быть представлена в виде разложения на элементарные дроби в следующем виде:
|
Q(x) |
= |
|
A1 |
+ |
|
A2 |
+ ...+ |
|
Aα1 |
+ ...+ |
|
B1 |
|
|
+ |
|
B2 |
|
+ ...+ |
|
Bαr |
|
|
+ |
|||||||||||
|
|
|
x − x |
(x |
− x )2 |
(x |
|
|
x − x |
|
|
(x |
− x |
)2 |
(x |
− x |
)αr |
|||||||||||||||||||
|
P(x) |
|
|
|
|
|
|
|
|
− x )α1 |
|
r |
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
r |
|
|
|
|
|
r |
|
|
|
||||
|
|
|
|
|
|
|
C1 x + D1 |
|
|
|
|
C2 x + D2 |
|
|
|
|
|
Cβ1 x + Dβ1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
+ |
|
|
|
+ |
|
|
|
+ ...+ |
|
|
+ ...+ |
|
|
|
|
|||||||||||||||||
|
|
|
|
x2 + p1 x + q1 |
|
(x2 + p1 x + q1 )2 |
(x2 + p x + q ) β1 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
E1 x + F1 |
|
|
|
+ |
|
|
E2 x + F2 |
+ ...+ |
|
|
|
Eβs x + Fβs |
, |
|
|
|
|
|
||||||||||||
где A1, A2 ,..., |
|
x2 + ps x + qs |
|
(x2 + ps x + qs )2 |
|
|
(x2 + ps x + qs )βs |
|
|
|
|
|
||||||||||||||||||||||||
Aα1 ,K, B1, B2 ,..., |
Bαr ,K, C1,C2 ,K, Cβ1 |
, D1, D2 ,K, Dβ1 ,K, E1, E2 ,K, Eβs |
, F1, F2 ,K, |
|||||||||||||||||||||||||||||||||
Fβs − некоторые числовые коэффициенты. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Для нахождения числовых коэффициентов |
Ai , Bi ,K, |
Ci , Di ,K, Ei , Fi при |
||||||||||||||||||||||||||||||||||
разложении дроби на элементарные применяют так называемый метод неопределённых коэффициентов, суть которого состоит в использовании понятия тождественно равных многочленов.
Определение 4.16. Два многочлена одинаковой степени называются тождественно равными, если их коэффициенты при одинаковых степенях переменной равны.
|
9x3 − 30x2 + 28x − 88 |
|
|
|
|
|
||||
Пример. Разложим дробь (x2 − 6x + 8)(x2 + 4) |
|
на элементарные. |
||||||||
Так как ( x2 − 6x + 8)(x2 + 4) = (x − 2)(x − 4)(x2 + 4) , то, по теореме 4.8, |
||||||||||
|
9x3 − 30x2 + 28x − 88 |
= |
A |
|
+ |
|
B |
+ |
Cx + D |
. |
|
|
x − |
2 |
|
x − 4 |
|
||||
|
(x − 2)(x − 4)(x2 + 4) |
|
|
|
x2 + 4 |
|||||
Приводя к общему знаменателю и приравнивая числители дробей справа и слева, получаем:
A(x − 4)(x2 + 4) + B(x − 2)(x2 + 4) + (Cx + D)(x2 − 6x + 8) = 9x3 − 30x2 + 28x − 88.
Раскрывая скобки слева в полученном равенстве и приводя подобные, приходим к равенству:
(A + B + C)x3 + (−4A − 2B − 6C + D)x2 + (4A + 4B + 8C − 6D)x + (−16A − 8B + 8D) =
= 9x3 − 30x2 + 28x − 88.
Пользуясь определением 4.16, получаем систему четырёх линейных
уравнений с четырьмя неизвестными
99
PDF created with pdfFactory Pro trial version www.pdffactory.com
ì |
A + |
B + C |
= 9, |
|
ï |
- 4A - |
2B - 6C + D = -30, |
||
ï |
||||
í |
4A + |
4B + 8C - 6D = 28, |
||
ï |
||||
ï |
|
|
+ 8D = -88, |
|
î-16A - 8B |
||||
решение которой, полученное, например, методом Гаусса, имеет вид
ìA = 5,
ïïB = 3,
íïC = 1.
ïîD = 2.
Искомое разложение имеет вид:
9x3 - 30x2 + 28x - 88 |
= |
5 |
+ |
3 |
+ |
x + 2 |
. |
|
(x - 2)(x - 4)(x2 + 4) |
x - 2 |
x - 4 |
x2 + 4 |
|||||
|
|
|
|
Пример. Разложим дробь 6x5 - 8x4 - 25x3 + 20x2 - 76x - 7 на элементарные.
3x3 - 4x2 -17x + 6
Так как дробь неправильная, то предварительно выделим у неё целую часть разделив уголком числитель на знаменатель:
6x5 - 8x4 - 25x3 + 20x2 - 76x - 7 |
= 2x2 + 3 + |
20x2 - 25x - 25 |
. |
|
3x3 - 4x2 -17x + 6 |
3x3 - 4x2 -17x + 6 |
|||
|
|
Разложим знаменатель дроби, полученной справа, на множители. Очевидно, при x = 3 многочлен 3x3 - 4x2 -17x + 6 обращается в нуль, поэтому многочлен 3x3 - 4x2 -17x + 6 делится на двучлен x − 3 без остатка (следствие 4.1). В результате указанного деления получим равенство:
3x3 - 4x2 -17x + 6 = (x - 3)(3x2 + 5x - 2).
Квадратный трёхчлен 3x2 + 5x - 2 имеет два действительных различных
корня x1 = -2 |
и x2 |
= |
1 |
. Поэтому кубический многочлен 3x3 - 4x2 -17x + 6 имеет |
|||||||||
3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
следующее разложение на линейные множители: |
|
|
|||||||||||
|
|
|
|
|
3x3 - 4x2 -17x + 6 = (x - 3)(x + 2)(3x -1). |
||||||||
Тогда правильная рациональная дробь |
|
|
|
||||||||||
|
|
|
|
|
20x2 - 25x - 25 |
|
= 5 |
× |
|
4x2 - 5x - 5 |
|
|
|
|
|
|
|
|
3x3 - 4x2 -17x + |
6 |
3x3 |
- 4x2 -17x |
+ 6 |
|
|||
|
|
|
|
|
|
|
|
||||||
имеет следующее разложение на элементарные дроби:
4x2 - 5x - 5 |
= |
A |
|
+ |
B |
|
+ |
C |
, |
|
3x3 - 4x2 -17x + 6 |
x - |
3 |
x + |
2 |
3x -1 |
|||||
|
|
|
|
откуда
A(x + 2)(3x -1) + B(x - 3)(3x -1) + C(x - 3)(x + 2) = 4x2 - 5x - 5.
Для того чтобы избежать при нахождении неопределённых коэффициентов раскрытия скобок, приведения подобных и решения системы уравнений, что в некоторых случаях может оказаться достаточно трудоёмким процессом, применяют так называемый метод произвольных
100
PDF created with pdfFactory Pro trial version www.pdffactory.com
