
Линейная алгебра и аналитическая геомерия
.PDF
3. Векторное произведение векторов ассоциативно относительно умножения вектора на число:
(m × a) ´ b = m × (a ´ b ).
4. Векторное произведение векторов дистрибутивно относительно сложения векторов:
a ×(b + с ) = a × b + a × с.
5. Векторное произведение векторов равно определителю матрицы
третьего порядка вида
|
|
|
|
|
|
|
|
|
|
|
|
|
a × |
|
|
i |
|
|
j |
k |
|
||||
|
= |
a1 |
a2 |
a3 |
, |
|||||||
b |
||||||||||||
|
|
|
b1 |
b2 |
b3 |
|
||||||
где a = (a1 , a2 , a3 ), b = (b1, b2 , b3 ).
6. Длина векторного произведения векторов численно равна площади параллелограмма, построенного на этих векторах как на сторонах
Из утверждения 6 теоремы 2.6 следует формула для вычисления площади треугольника АВС:
S ABC = 12 AB ´ AC .
Заметим, что последнюю формулу можно применять к любым векторам, образующим стороны треугольника, с началом в общей вершине.
Пример. Найти векторное произведение векторов |
|
|
|
|
|
|
|
||||||||
a = 2i |
+ 5 j + k и |
||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= i |
+ 2 j - 3k . |
|
|
|
|
|
|
|
||||||
Векторы a и b имеют координаты: a = (2, 5, 1), b = (1, 2, -3). Применяя утверждение 5 теоремы 2.6, получим:
i j k
a ´ b = 2 5 1 = -17i + 7 j - k. 1 2 - 3
Пример. Вычислить площадь треугольника АВС с вершинами А(2, 2, 2),
В(4, 0, 3), С(0, 1, 0).
AB |
= (4 - 2, 0 - 2, 3 - 2) = (2, - 2, 1), |
|
|
AC |
= (0 - 2, 1- 2, 0 - 2) = (-2, -1, - 2). |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
k |
|
|
|
|
|
|
|
|||||
|
|
|
´ |
|
= |
2 - 2 |
|
1 |
|
|
|
|
|
|
|
|||||||
|
|
AB |
AC |
|||||||||||||||||||
|
|
|
= -5i |
- 2 j + 6k. |
||||||||||||||||||
|
- 2 |
-1 |
- 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB ´ AC = 
 25 + 4 + 36 =
25 + 4 + 36 = 
 65.
65.
S ABC = 
 265 (кв. ед).
265 (кв. ед).
41
PDF created with pdfFactory Pro trial version www.pdffactory.com

Пример. Найти площадь параллелограмма, построенного на |
векторах |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
a + 3 |
|
, 3a + |
|
как на сторонах, если |
|
a |
|
= |
|
|
|
|
= 1; |
|
a ^ |
|
= 300. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
b |
b |
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Применяя утверждения теоремы 2.6, получим: |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 9 × (b ´ a) + 3× (b |
´ b ) = -b ´ a + 9 × (b ´ a) = 8 |
× (b ´ a), |
||||||||||||||||||||||||||||||||
(a + 3b ) ´ (3a + b ) = 3× (a ´ a) + a ´ b |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
откуда Sпараллелограмма = 8× |
|
|
|
|
|
× |
|
a |
|
×sin 300 = 4 (кв. ед). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
2.6. Смешанное произведение векторов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Определение 2.14. Смешанным произведением векторов a , |
|
|
|
и c |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
называется число, обозначаемое символами a × |
|
×c |
или (a , |
|
, c ) |
и равное |
|||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
скалярному произведению вектора a на |
вектор, |
равный векторному |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
произведению векторов |
|
и c : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a × |
|
× c = a ×( |
|
´ c). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
b |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Основные |
|
свойства |
смешанного |
|
|
|
произведения |
векторов |
||||||||||||||||||||||||||||||||||||||||||||||
сформулированы в следующей теореме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
Теорема 2.7. Справедливы следующие утверждения:
1.Смешанное произведение векторов равно в том и только в том случае, если:
1)хотя бы один из векторов нулевой;
2)какие-либо два векторов коллинеарны;
3)векторы компланарны.
2.Смешанное произведение векторов ассоциативно:
(a ´b ) ×c = a ×(b ´c).
3. Смешанное произведение векторов не меняется при циклической перестановке его сомножителей, а при перестановке двух соседних
сомножителей смешанное произведение векторов меняет свой знак на противоположный:
(a,b,c) = (b,c,a) = (c, a,b ) = -(b ,a,c) = -(c,b, a) = -(a,c,b ).
4. Смешанное произведение векторов обладает свойством линейности:
(λa1 + μa2 ,b,c) = λ(a1,b ,c) + μ(a2 ,b ,c)
5. Смешанное произведение векторов равно определителю матрицы,
строки которой составлены из координат его соответствующих сомножителей:
a1 a2 a3
(a,b ,c) = b1 b2 b3 , c1 c2 c3
42
PDF created with pdfFactory Pro trial version www.pdffactory.com
где a = (a1 , a2 , a3 ), |
|
= (b1, b2 , b3 ), c = (c1, c2 , c3 ). |
|
|
||
b |
|
|
||||
6. Модуль смешанного произведения a × |
|
×c |
|
численно равно объёму |
||
b |
||||||
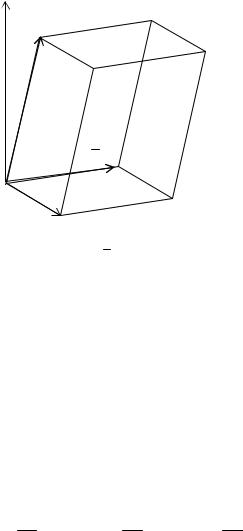
параллелепипеда, построенного на векторах a , |
|
и c как на рёбрах (рис. |
||||
b |
||||||
11) |
|
|
|
|
|
|
a
b
c
Рисунок 11. Параллелепипед, построенный на векторах a , b и c как на рёбрах
Из утверждения 6 теоремы 2.7 и стереометрических соотношений между телами следует, что объём треугольной пирамиды (тетраэдра), DABC, численно равен
V = |
1 |
|
|
( |
|
, |
|
, |
|
) |
|
. |
|
|
AB |
AC |
AD |
|
|||||||||
|
|||||||||||||
DABC |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что последнюю формулу можно применять к любым векторам, образующим рёбра пирамиды, с началом в общей вершине.
Пример. Доказать, что точки А(5, 7, 2), B(3, 1, -1), C(9, 4, -4), D(1; 5, 0)
принадлежат одной плоскости.
Воспользуемся утверждениями 1(3) и 5 теоремы 2.7. Для этого составим векторы:
AB = (-2,-6, 1), AC = (4,-3,-2), AD = (-4,-2, 2).
Найдём смешанное произведение полученных векторов:
|
|
- 2 |
- 6 |
1 |
|
|
|||||
|
|
||||||||||
|
× |
|
× |
|
= |
|
4 - 3 |
- 2 |
|
= 0, |
|
AB |
AC |
AD |
|||||||||
|
|
- 4 |
- 2 |
2 |
|
|
|||||
следовательно, составленные выше векторы компланарны, поэтому точки A, B, C, D принадлежат одной плоскости.
Пример. Найти объём пирамиды, если её вершины заданы координатами
A(0, 0, 1), B(2, 3, 5), C(6, 2, 3), D(3, 7, 2).
43
PDF created with pdfFactory Pro trial version www.pdffactory.com

Воспользуемся формулой VDABC = 16 (BA, BC, BD). Для этого составим
векторы:
BA = (-2, - 3, - 4), BD = (1, 4, - 3), BC = (4, -1, - 2).
Тогда объём пирамиды
V |
|
1 |
|
|
- 2 |
- 3 |
- 4 |
|
= 20 (куб ед). |
|
|
|
|
||||||||
= |
× mod |
|
1 |
4 |
- 3 |
|
||||
|
||||||||||
DABC |
6 |
|
|
|
|
|
|
|
||
|
|
|
4 |
-1 |
- 2 |
|
|
|||
|
|
|
|
|
|
|
||||
Вопросы для самоконтроля к разделу «Элементы векторной алгебры»
1.Что такое вектор и его длина? Какой вектор называется нулевым?
2.Какие векторы называются коллинеарными, а какие – компланарными?
3.Какие операции с векторами называются линейными? Сформулируйте их основные свойства.
4.Что называется базисом система векторов? Как определяются координаты вектора в некотором базисе?
5.Какие векторы называются линейно независимыми, а какие – линейно зависимыми? Сформулируйте свойства линейно зависимых и линейно независимых систем векторов.
6.Что называется системой координат? Как определяется декартова система координат на плоскости и в пространстве?
7.Сформулируйте определения ортонормированного базиса системы векторов и прямоугольной декартовой системы координат на плоскости и в пространстве?
8.Как определяются полярная, цилиндрическая и сферическая системы координат? Запишите формулы связи соответствующих координат точки с её прямоугольными декартовыми координатами.
9.Как определяется вектор и его длина в координатной форме?
Сформулируйте правила вычисления координат суммы векторов и произведения вектора на число.
10.Запишите формулы деления отрезка в данном отношении. Как вычисляются координаты середины отрезка?
11.Перечислите типы произведений векторов, сформулируйте их определения и основные свойства.
Задачи для самостоятельного решения к разделу «Элементы векторной алгебры»
1. Векторы a = (3, 2, 2), b = (2, 1, −1), c = (−1, 0, 3), d = (1, 2, 3) заданы в некотором базисе. Выясните, образуют ли сами векторы a, b и с
44
PDF created with pdfFactory Pro trial version www.pdffactory.com

|
базис. В случае утвердительного ответа найдите координаты вектора |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
в этом базисе. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2. |
Вычислите |
скалярное |
произведение |
векторов |
2a − 5 |
|
|
|
|
|
|
|
|
|
и |
|
3a + 7 |
|
|
, если |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
известно, что |
|
a |
|
= 3, |
|
|
|
|
|
= 4, |
a |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
b |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
3. |
Вычислите угол между векторами |
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, если a = 2i |
− j + 5k , |
b = −i + 2 j + 3k . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
Вычислите скалярное произведение 3a + 2 |
|
|
и 6a − |
|
, если |
известно, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
b |
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
a |
|
= 1, |
|
|
|
|
= 2, |
ϕ = |
π . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
Выясните, |
при |
|
|
каком |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
значении λ векторы a = i |
+ j + λk |
|
|
b = i + 2 j + 6k |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ортогональны. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
6. |
Вычислите |
скалярное |
произведение |
|
векторов |
|
a + 2 |
|
+ 3 |
|
|
|
и |
|
4a + 5 |
|
+ 6c, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
b |
c |
|
|
b |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
если известно, что |
|
a |
|
= 1, |
|
|
|
= 2, |
|
|
|
= 3, |
a^ |
|
= |
π , a^ |
|
= π , |
|
^ |
|
= π . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
b |
|
|
|
c |
b |
c |
b |
c |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
a = 2i − 3 j + 2k и b = 2i − 2 j + 3k.
8.Вычислите площадь треугольника АВС с вершинами А(1, 2, 3), В(0, 1, 0),
С(3, 3, -5).
9. Вычислите площадь параллелограмма, построенного на векторах
a + 2 |
|
, 3a + 4 |
|
как на сторонах, если известно, что |
|
a |
|
= 1, |
|
|
|
= 2, |
|
a^ |
|
= 450. |
b |
b |
|
|
b |
b |
|||||||||||
10. Вычислите смешанное произведение векторов a = (1,− 2, 3), |
|
= (2, 1,− 3) и |
||||||||||||||
b |
||||||||||||||||
c= (4, 1, 0).
11.Выясните, принадлежат ли точки А(2, 4, 1), B(3, -1, 1), C(0, 1, -3) и D(-1, -6, 2) одной плоскости.
12.Вычислите объём пирамиды, если её вершины заданы координатами
A(0, 1, 2), B(2, 0, 1), C(1, 4, 1), D(1, 2, 6).
3. Элементы аналитической геометрии
3.1. Линии на плоскости
Определение 3.1. Уравнением линии на плоскости называется соотношение y = f (x) между прямоугольными декартовыми координатами
точек, составляющих эту линию.
Если первоначально дана некоторая линия на плоскости, то, формулируя аналитически свойство, определяющее эту линию, можно получить уравнение этой линии. При этом следует учитывать, что каждое уравнение можно переписать в различных равносильных формах. Это
даёт возможность взамен линий рассматривать их уравнения и тем самым сводить геометрические задачи к алгебраическим. Например, для того чтобы проверить, проходит линия с уравнением y = f (x) через некоторую
45
PDF created with pdfFactory Pro trial version www.pdffactory.com
точку M (xM , yM ), достаточно подставить координаты этой точки в уравнение линии и проверить удовлетворится ли оно, т.е. будет ли yM = f (xM ).
3.1.1. Прямая на плоскости
Определение 3.2. Прямой l на плоскости называется линия, заданная
уравнением первого порядка вида
Ax + By + C = 0, |
(3.1) |
где A, B, C − действительные числа ( A и B − коэффициенты, |
C − свободный |
член), причём коэффициенты не равны нулю одновременно, т.е. A2 + B2 ¹ 0. |
|
Уравнение (3.1) называется общим уравнением прямой. |
Запись вида |
l : Ax + By + C = 0 читается так: «прямая l имеет уравнение Ax + By + C = 0) .
В зависимости от значений постоянных A, B, C возможны следующие
частные случаи расположения прямой относительно прямоугольной декартовой системы координат:
1)C = 0, А ¹ 0, В ¹ 0 – прямая l проходит через начало координат;
2)А = 0, В ¹ 0, С ¹ 0 – прямая l параллельна оси Ох;
3)В = 0, А ¹ 0, С ¹ 0 – прямая l параллельна оси Оу;
4)В = С = 0, А ¹ 0 – прямая l совпадает с осью Оу;
5)А = С = 0, В ¹ 0 – прямая l совпадает с осью Ох.
Уравнение прямой может быть представлено в различных видах в зависимости от каких–либо заданных начальных условий. Рассмотрим различные способы составления уравнения прямой на плоскости.
3.1.1.1. Уравнение прямой по точке и вектору нормали
Определение 3.3. |
Вектор nl = (A, B), перпендикулярный |
прямой l, |
|
называется вектором нормали этой прямой. |
|
|
|
Уравнение прямой l, проходящей через точку |
Mo (xo , yo ) |
||
перпендикулярно вектору nl = (A, B), имеет вид: |
|
|
|
|
A(x - xo ) + B(y - yo ) = 0. |
|
(3.2) |
Пример. Составим уравнение прямой, проходящей через точку |
А(1, 2) |
||
перпендикулярно вектору n = (3, −1). |
|
|
|
Подставляя в |
уравнение (3.2) значения A = 3, B = −1, |
xo =1, |
yo = 2, |
раскрывая скобки и приводя подобные члены, получим общее уравнение
3x − y −1 = 0.
46
PDF created with pdfFactory Pro trial version www.pdffactory.com

3.1.1.2. Уравнение прямой, проходящей через две точки
Пусть на плоскости заданы две точки A(xA , yA ), B(xB , yB ), уравнение прямой l, проходящей через эти точки, имеет вид:
x - xA = y - yA . xB - xA yB - yA
Уравнение (3.3) приводится к виду
y - yA = yB - yA (x - xA ), если xB ¹ xA , xB - xA
тогда
(3.3)
(3.3a)
и |
|
x - xA , если xB = xA. |
(3.3б) |
Определение 3.4. Число k = yB - yA называется угловым коэффициентом xB - xA
прямой l, проходящей через точки A(xA , yA ) и B(xB , yB ).
Пример. Составить уравнение прямой, проходящей через точки А(1, 2) и
В(3, 4).
Применяя формулу (3.3a), получаем:
y- 2 = 43--12 (x -1), y - 2 = x -1,
т.е. общее уравнение прямой имеет вид x − y + 1 = 0.
3.1.1.3. Уравнение прямой по точке и угловому коэффициенту
Общее уравнение прямой (3.1) приведём к виду
y = - BA x - CB
и обозначим - |
A |
= k, |
- C |
= b. |
|
B |
|
||||
|
|
B |
|
|
|
Определение 3.5. Уравнение прямой l, записанное в виде |
(3.4) |
||||
|
|
|
|
y = kx + b, |
|
называется уравнением прямой с угловым коэффициентом k.
Для составления уравнения прямой в виде (3.4) достаточно знать значение её углового коэффициента k, а также координаты какой-либо
точки этой прямой.
Тангенс угла наклона прямой l к оси абсцисс равен угловому коэффициенту (рис.12):
47
PDF created with pdfFactory Pro trial version www.pdffactory.com
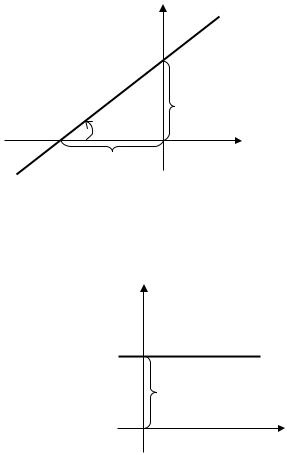
tgα = k.
y
l
|
|
b |
α |
|
|
a |
O |
x |
Рисунок 12. Прямая l образует угол α
с положительным направлением оси абсцисс
Если k = 0, то прямая l параллельна оси абсцисс, и её уравнение
имеет вид y = b (рис. 13)
y
l
b
O |
x |
Рисунок 13. Прямая l параллельна оси абсцисс
Пример. Прямая задана общим уравнением 4x + 2y − 2 = 0. Составим для
этой прямой уравнение с угловым коэффициентом.
Для этого перенесём в правую часть с противоположным знаком 4x и свободный член − 2 , затем разделим обе части полученного уравнения на коэффициент перед y :
2y = −4x + 2, y = −2x +1,
откуда k = −2, b = 1.
3.1.1.4. Уравнение прямой по точке и направляющему вектору
Определение 3.6. Каждый ненулевой вектор аl = (a1 , a2 ), лежащий на прямой l, либо на прямой, ей параллельной, называется направляющим вектором прямой l.
48
PDF created with pdfFactory Pro trial version www.pdffactory.com

Если вектор |
аl = (a1 , a2 )- |
направляющий вектор прямой |
l |
с |
общим |
|||||
уравнением (3.1), то его координаты удовлетворяют условию |
|
|
|
|
||||||
|
|
A × a1 + B ×a2 = 0. |
|
|
|
|
||||
Уравнение прямой l, проходящей через точку |
M o (xo , yo ), |
с |
||||||||
направляющим вектором аl = (a1 , a2 ), имеет вид: |
|
|
|
|
||||||
|
|
|
x - xo |
= |
y - yo |
. |
|
|
(3.5) |
|
|
|
|
a1 |
|
|
|
||||
|
|
|
|
a2 |
|
|
|
|
||
Пример. Найти уравнение прямой с направляющим вектором |
аl = (1,-1), |
|||||||||
проходящей через точку Mo (1, 2). |
|
|
|
|
|
|
|
|||
Подставляя |
исходные |
данные |
задачи xo =1, yo = 2, a1 =1, a2 |
= -1 |
в |
|||||
уравнение (3.5), выполняя необходимые арифметические операции, получим общее уравнение прямой:
x + y − 3 = 0.
3.1.1.5. Уравнение прямой в отрезках
Если в общем уравнении прямой (3.1) свободный член С¹0, то, разделив (3.1) на –С, получим:
|
|
|
- |
А |
|
х - |
|
В |
у = 1 |
|
||
|
|
|
С |
|
|
|
||||||
или |
|
|
|
|
|
С |
|
|||||
|
|
|
|
x |
|
y |
|
|
|
|||
|
|
|
|
|
+ |
= 1, |
(3.6) |
|||||
где a = - C |
|
b = - C |
|
|
a |
b |
||||||
|
|
|
|
|
|
|
||||||
, |
. Геометрический смысл чисел a и b |
заключается в том, |
||||||||||
A |
|
B |
|
|
|
|
|
|
|
|
|
|
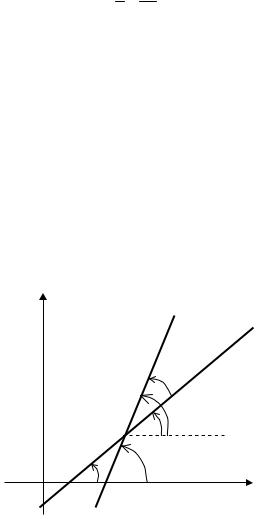
что a является абсциссой точки пересечения прямой с осью абсцисс, а b – ординатой точки пересечения прямой с осью ординат (рис. 14). Определение 3.7. Уравнение прямой l, записанное в виде (3.6),
называется уравнением прямой в отрезках.
y
l
b
a |
O |
x |
Рисунок 14. Прямая l отсекает a единиц на оси абсцисс и b единиц на оси ординат
49
PDF created with pdfFactory Pro trial version www.pdffactory.com
Пример. Для прямой с общим уравнение x − y −1= 0 уравнение в отрезках
имеет вид:
1х + −у1 =1,
т.е. эта прямая отсекает 1 единицу на оси абсцисс и -1 единицу на оси ординат.
Cледует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат, нельзя.
3.1.1.6.Угол между прямыми на плоскости. Условия параллельности
иперпендикулярности прямых на плоскости
Определение 3.8. Углом между двумя прямыми называется тот из двух углов, образованных этими прямыми, который меньше развёрнутого.
Если заданы две прямые l1 : y = k1x + b1 и |
l2 : y = k2 x + b2 , то угол φ между |
||||||||
ними изображён на рис.15 |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l1 |
||
|
|
φ |
|
|
|
|
|||
|
|
|
α2 |
|
|
|
|
||
|
|
α1 |
|
|
|
|
|
|
|
|
α1 |
α2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
O |
|
|
|
|
|
|
x |
||
Рисунок 15. |
Угол между прямыми l1 и l2 |
||||||||
Поскольку k1 = tgα1 и k2 |
= tgα2 , |
то из |
геометрических соображений, |
||||||
приведённых на рис.15, следует, что |
|
|
|
|
|
|
|
||
α2 = α1 +ϕ, ϕ = α2 −α1 , |
|||||||||
откуда |
|
|
|
tgα2 − tgα1 |
|
||||
tgϕ = tg (α2 −α1 ) = |
|
||||||||
1 |
+ tgα1tgα2 |
||||||||
|
|
|
|||||||
или |
|
k2 − k1 |
|
|
|
||||
|
tgϕ = |
. |
(3.7) |
||||||
|
|
||||||||
|
|
1+ k k |
2 |
|
|
|
|||
|
|
|
1 |
|
|
|
|||
Пример. Две прямые заданы уравнениями y = 2x + 3 и y = −3x + 2. Вычислим угол между этими прямыми.
50
PDF created with pdfFactory Pro trial version www.pdffactory.com
