
3. Замена базиса линейного пространства.
Пусть в пространстве Rn заданы два базиса е1,е2, ... ,еn и f1, f2, f3…, fn, тогда каждый вектор из базиса f можно разложить по базису e, т.е.
![]()
![]()
Из координатных столбцов векторов fj в базисе e можно составить квадратную матрицу порядка n.
 ,
которая называется, матрицей перехода
от базиса e
к базису f.
,
которая называется, матрицей перехода
от базиса e
к базису f.
Она
является невырожденной, т.е. А0.
Значит, выражение
![]() можно записать в матричном виде
можно записать в матричном виде![]() .
Умножая это равенство наТ-1
справа, получаем
.
Умножая это равенство наТ-1
справа, получаем
fT-1=e или e = fT-1, т.е. Т-1 – матрица перехода от базиса f к базису e.
Пример
5.
Найти координаты вектора
![]() в базисе
в базисе![]() если он задан в базисе
если он задан в базисе![]() .
.

![]() .
.
Решение. При переходе от базиса e к базису f координаты одного и того же вектора связаны формулами:
![]() ,
,
![]() ,
,
где T матрица перехода, которая находится из равенства f = eT.
Здесь
 .
Найдем определитель матрицы:
.
Найдем определитель матрицы:
![]()
(формула разложения определителя по третьей строке).
Найдем
алгебраические дополнения к элементам
матрицы T
и обратную матрицу по формуле
![]() :
:
![]()
![]()
![]() .
.
Таким
образом, обратная матрица будет
 и, следовательно,
и, следовательно,
 .
.
Окончательно
имеем в базисе f:
![]() .
.
Зависимость между матрицами одного и того же оператора в разных базисах выражается теоремой.
Теорема. Матрицы А и А* линейного оператора А(х) в базисах е1,е2, ... ,еn и f1, f2, f3…, fn связаны соотношением
A* = Т-1∙A∙Т,
где Т — матрица перехода от старого базиса к новому.
Пример
6.
В базисе e1,
e2
оператор А
имеет матрицу
![]() .
Найти матрицу этого же оператора в новом
базисеf1,
f2
, где
.
Найти матрицу этого же оператора в новом
базисеf1,
f2
, где
![]() .
.
Решение:
составим матрицу перехода (координаты
векторов нового базиса являются столбцами
матрицы перехода) т.е.
![]() и найдем обратную матрицу Т-1.
Т=5,
и найдем обратную матрицу Т-1.
Т=5,
![]() .
.
![]() -
матрица оператора А
в новом базисе.
-
матрица оператора А
в новом базисе.
Пример
7. Найти
матрицу линейного преобразования
![]() в базисе
в базисе![]() если она задана в базисе
если она задана в базисе![]()
 ,
,
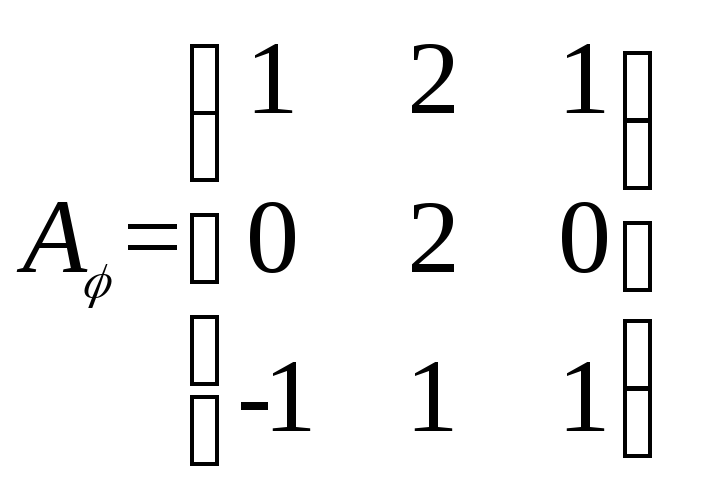 .
.
Решение. При переходе от базиса e к базису f матрица линейного преобразования, в соответствии с определением, будет иметь вид
![]() ,
,
где T матрица перехода, которая находится из равенства f = eT.
Здесь
 .
.
Найдем
определитель матрицы:

(прибавили к элементам второго и третьего столбца соответствующие элементы первого столбца и записали формулу разложения определителя по первой строке).
Найдем
алгебраические дополнения к элементам
матрицы T
и обратную матрицу по формуле
![]() :
:
![]()
 .
.
Таким
образом, обратная матрица будет
 и, следовательно,
и, следовательно,


 .
.
Лекция 14. Собственные значения и собственные векторы линейного оператора.
ЗАДАЧА.
Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей

Определение 1. Ненулевой вектор X, удовлетворяющий условию
AX=X , (1)
называется собственным вектором преобразования A . Число в равенстве (1) называется собственным значением.
Из определения следует, что собственный вектор под действием линейного оператора А переходит в вектор, коллинеарный самому себе, т.е. просто умножается на некоторое число. В то же время несобственные векторы преобразуются более сложным образом. В связи с этим понятие собственного вектора является очень полезным и удобным при изучении многих вопросов матричной алгебры и ее приложений.
Равенство (1) записано в матричной форме: АХ = Х,
где X — матрица-столбец из координат вектора х, или в развернутом виде
 (1)
(1)
Перепишем систему так, чтобы в правых частях были нули:
 (2)
(2)
Или в матричном виде (А - Е) = 0.
Полученная однородная система всегда имеет нулевое решение х = 0 = (0,0,...,0). Для существования ненулевого решения необходимо и достаточно, чтобы определитель системы (2) был равен 0.
 (3)
(3)
Определитель |А – ХЕ| является многочленом n-й степени относительно X. Этот многочлен называется характеристическим многочленом оператора А или матрицы А, а уравнение (3) — характеристическим уравнением оператора А или матрицы А.
Для отыскания собственных векторов необходимо:
1) составить характеристическое уравнение (3) и найти его корни 1, 2, 3 т.е. собственные значения;
2)
составить систему (2), положив
равным одному из найденных собственных
значений, например:
= 1,
и найти ненулевое решение
![]() этой системы;
этой системы;
3)
записать вектор
![]() который является собственным вектором
данного преобразования, соответствующим
собственному значению1
;
который является собственным вектором
данного преобразования, соответствующим
собственному значению1
;
4) проделать шаги 2), 3) для = 2 и = 3.
Следует
иметь в виду, что собственные векторы
определяются с точностью до произвольного
множителя, т.е. если вектор X
- собственный, то и вектор
![]() - собственный.
- собственный.
Собственные векторы, соответствующие различным собственным значениям, линейно независимы.
Если линейное преобразование имеет S одинаковых собственных чисел 0 , то говорят, что 0 имеет кратность S. Тогда ему соответствует не более S линейно независимых собственных векторов.
Пример 1. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
 .
.
РЕШЕНИЕ.
Запишем характеристическое уравнение данного линейного преобразования и найдем его корни:

Чтобы решить это уравнение, необходимо раскрыть определитель. Для этого рекомендуется разложить определитель по элементам некоторой строки (столбца), предварительно получив в этой строке (столбце) два нуля, используя свойства определителей. В нашем случае сначала к первой строке прибавим вторую, получим

Теперь ко второму столбцу прибавим первый, умноженный на (-1):
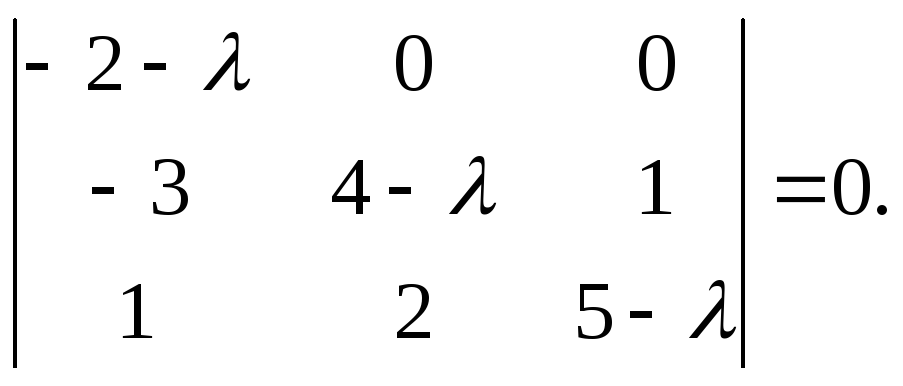
Раскладывая этот определитель по элементам первой строки, получаем:
![]()
или
![]()
Корнями этого уравнения являются три числа, 1 = -2, 2 = 3, 3 = 6.
В системе (2) положим = 1 = -2, тогда она примет вид:
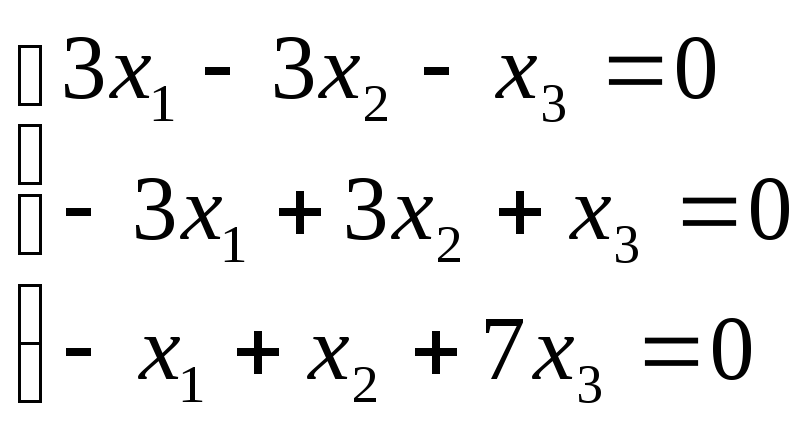
Здесь первые два уравнения тождественны, поэтому одно из них можно отбросить

Применяя метод Гаусса, найдем общее решение этой системы:
![]()
Следовательно, первым собственным вектором, соответствующим = -2, является X1 = (p1 , p1 , 0) = p1 (1,1,0), p1 0.
Меняя p1 ,будем получать различные векторы, лежащие на одной прямой. Все они собственные.
Аналогично поступаем с собственными значениями 2 = 3, 3 = 6, т.е. находим соответствующие им собственные векторы
X2 = p2(1 , -1 , 1); p2 0, (2 = 3);
X3 = p3(1 , -1 , -2); p3 0, (3 = 6).
Собственные вектора X1, X2, X3 определены с точностью до произвольных чисел p1 , p2 , p3 .
Пример 2. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
 .
.
РЕШЕНИЕ
Характеристическое уравнение данного преобразования имеет вид
 .
.
Корни этого уравнения 1 = 2 = -1, 3 = 5 являются собственными значениями.
Чтобы найти собственный вектор, соответствующий 1 = 2 = -1, полагаем в системе (2) = -1. Получим

Все
три уравнения тождественны, поэтому
два из них могут быть отброшены. Оставшееся
уравнение
![]() содержит три неизвестные. Полагая
содержит три неизвестные. Полагая
![]() =p1
,
=p1
,
![]() =p2
, находим
=p2
, находим
![]() = -p1
– p2
.
= -p1
– p2
.
Вектор X1 = (-p1 – p2 , p1 , p2 ), где p1 и p2 - любые числа, одновременно не равные нулю, является собственным вектором линейного преобразования, соответствующим 1 = 2 = -1.
Аналогично находим, что вектор X2 = p3(1, 1, 1) является собственным вектором данного преобразования, соответствующим 3=5.
Пример 3. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей
 .
.
РЕШЕНИЕ.
Характеристическое уравнение данного преобразования
 .
.
Корни этого уравнения 1 = 2 = 3 = 1 являются собственными значениями.
Полагаем в системе (2) = 1:
 .
.
Все
три уравнения тождественны, поэтому,
отбросив два из них, имеем
![]() .
.
Полагая
![]() ,
находим
,
находим
![]() .
.
Вектор X = (5q – 2p; p; q), где p, q - любые числа, одновременно не равные нулю, является собственным вектором данного линейного преобразования.
Пример4. Найти собственные
значения и собственные векторы
преобразования![]() ,
заданного в некотором базисе матрицей
,
заданного в некотором базисе матрицей .
.
Решение. Найдем собственные числа этой матрицы, для чего составим и решим характеристическое уравнение:

![]()
Приравняв к нулю это выражение, находим:
![]()
Находим
собственные векторы, соответствующие
найденным собственным значениям, для
чего при каждом
![]() составляем и решаем систему:
составляем и решаем систему:
а)
при
![]() ,
получаем
,
получаем

что
равносильно системе (здесь
![]() )
)
 ,
,
полагая
в которой, например,
![]() ,находим
,находим![]() ,таким образом, собственный вектор,
соответствующий собственному значению
3 есть
,таким образом, собственный вектор,
соответствующий собственному значению
3 есть
![]()
б)
при
![]() ,
получаем
,
получаем

что
равносильно уравнению (здесь
![]() ):
):![]() ,
,
полагая
в котором сначала,
![]() ,а затем
,а затем
![]() получаем еще два линейно независимых
собственных вектора:
получаем еще два линейно независимых
собственных вектора:
![]() .
.
Лекция 15. Привидение квадратной матрицы к диагональному виду.
Наиболее простой вид принимает матрица А линейного оператора А, имеющего n линейно независимых собственных векторов el,e2,...,en с собственными значениями, соответственно равными 1, 2, 3, ... n. Векторы е1, е2, ... , en примем за базисные. Тогда A(ei) = iei (i = 1,2,..., n) или
A(еi) = a1ie1 + a2ie2 + ... + aiiei + ... + anien = iei,
откуда aij = 0, если i j, и аij = i, если i = j. Таким образом, матрица оператора А в базисе, состоящем из его собственных векторов, является диагональной и имеет вид:
 .
.
Верно и обратное: если матрица А линейного оператора А в некотором базисе является диагональной, то все векторы этого базиса — собственные векторы оператора А.
Можно доказать, что если линейный оператор имеет n попарно различных собственных значений, то отвечающие им собственные векторы линейно независимы, и матрица этого оператора в соответствующем базисе имеет диагональный вид.
Пример
1.
Привести
матрицу А
=
![]() линейного оператора
А
к
диагональному виду.
линейного оператора
А
к
диагональному виду.
Решение.
Найдём собственные значения и
собственные векторы линейного оператора
А,
заданного матрицей
![]() .
.
Составляем характеристическое уравнение
![]()
![]() или
2
-
2
- 35
= 0 ,
откуда
собственные значения линейного оператора
А
1
= -5,
2
= 7.
или
2
-
2
- 35
= 0 ,
откуда
собственные значения линейного оператора
А
1
= -5,
2
= 7.
Находим собственный вектор х(1) = (х1, х2), соответствующий собственному значению 1 = -5. Для этого решаем матричное уравнение
 или
или
 ,
,
откуда находим х2 = -1,5х1. Положив х1 = с, получим, что векторы х(1) = (с; -1,5с) при любом с 0 являются собственными векторами линейного оператора А с собственным значением 1 = -5.
Аналогично
можно убедиться в том, что векторы х(2)
=
![]() при
любом с1
0
являются собственными векторами
линейного
оператора
А
с
собственным значением 2
= 7
.
при
любом с1
0
являются собственными векторами
линейного
оператора
А
с
собственным значением 2
= 7
.
Так
как координаты
векторов х(1
)и
x(2)
не пропорциональны, то векторы х(1)
и х(2)
линейно
независимы. Поэтому в базисе, состоящем
из любых
пар собственных векторов x(1)
= (с; -1,5с)
и х(2)
=
![]() (т.е.
при любых с0,
c1
0,
например, при с
= 2,
c1
= 6 из векторов
x(1)
= (2; - 3) и х{2)
= (4;
6) и т.д.) матрица А
будет
иметь диагональный
вид:
(т.е.
при любых с0,
c1
0,
например, при с
= 2,
c1
= 6 из векторов
x(1)
= (2; - 3) и х{2)
= (4;
6) и т.д.) матрица А
будет
иметь диагональный
вид:
 или
или
![]() .
.
Это
легко проверить, взяв, например, в
качестве нового базиса линейно
независимые собственные векторы х(1)
= (2; - 3) и x(2)
=
(4; 6). Действительно, матрица С
перехода от старого базиса
к новому в этом случае будет иметь
вид C
= (x(1),
x(2))
=
![]() .
Тогда
матрица А
в
новом
базисе х(1),
x(2)
примет вид:
.
Тогда
матрица А
в
новом
базисе х(1),
x(2)
примет вид:
![]() .
.
Или
после вычислений
![]() ,
т.е.
получим ту же диагональную матрицу,
элементы которой по главной диагонали
равны собственным значениям матрицы
А.
,
т.е.
получим ту же диагональную матрицу,
элементы которой по главной диагонали
равны собственным значениям матрицы
А.
Пример2.Пусть линейный оператор![]() ,
действующий в евклидовом пространстве
,
действующий в евклидовом пространстве
![]() ,
имеет в ортонормированном базисе матрицу
,
имеет в ортонормированном базисе матрицу![]() .
Построить в этом векторов пространстве
базис из собственных оператора
.
Построить в этом векторов пространстве
базис из собственных оператора![]() и найти матрицу оператора
и найти матрицу оператора![]() в этом базисе.
в этом базисе.
 .
.
Решение.
1)
Найдем
собственные числа оператора
![]() ,
для чего составим и решим характеристическое
уравнение:
,
для чего составим и решим характеристическое
уравнение:

![]()
![]()
![]()
![]()
Приравняв
к нулю, находим:
![]()
2)
Находим собственные векторы, соответствующие
найденным собственным значениям, для
чего при каждом
![]() составляем и решаем систему:
составляем и решаем систему:
а)
при
![]() ,
получаем
,
получаем

что
равносильно системе (здесь
![]() )
)
 ,
,
полагая
в которой, например,
![]() ,
находим
,
находим
![]() ,
таким образом, собственный вектор,
соответствующий собственному значению
9 есть
,
таким образом, собственный вектор,
соответствующий собственному значению
9 есть
![]()
б) при
![]() ,получаем
,получаем ,
,
что
равносильно уравнению (здесь
![]() )
)
![]() ,
,
полагая
в котором сначала,
![]() ,а затем
,а затем
![]() получаем еще два линейно независимых
собственных вектора:
получаем еще два линейно независимых
собственных вектора:
![]() .
.
3)
Находим матрицу перехода к базису из
собственных векторов и обратную к ней
(столбцами матрицы перехода являются
координатные столбцы векторов
![]() (см. раздел
1)):
(см. раздел
1)):
 .
.
![]()
![]()
![]()
4)
Теперь по формуле (5.1) находим
![]() – матрицу
линейного оператора в базисе из
собственных векторов
– матрицу
линейного оператора в базисе из
собственных векторов


Таким образом, матрица линейного оператора в базисе из собственных векторов диагональная!
Лекция 16. Квадратичные формы.
При решении различных прикладных задач часто приходится исследовать квадратичные формы.
Определение 1. Квадратичной формой L(х1,х2,...,хn) от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
L(х1,
х2,...,хn)
=
![]() .
.
Определение 2. Предполагаем, что коэффициенты квадратичной формы aij — действительные числа, причем aij = aji. Матрица А = (аij) (i, j = 1, 2, ..., n), составленная из этих коэффициентов, называется матрицей квадратичной формы.
Определение 3. Матрица, у которой все элементы аij = аji , называется симметрической.
В матричной записи квадратичная форма имеет вид: L = ХТАХ,
где
X
—
матрица-столбец переменных.
или  .
.
Пример 1. Дана квадратичная форма L(x1, х2, х3) = 4х12 - 12х1х2 - 10х1х3 + х22 - 3x32. Записать ее в матричном виде.
Решение. Найдем матрицу квадратичной формы. Ее диагональные элементы равны коэффициентам при квадратах переменных, т.е. 4, 1, —3, а другие элементы — половинам соответствующих коэффициентов квадратичной формы. Поэтому
 ►
►
Выясним, как изменяется квадратичная форма при невырожденном линейном преобразовании переменных.
Пусть матрицы-столбцы переменных X = (х1,х2,...,хn)Т и
Y = (y1,y2, ... ,yn)Т связаны линейным соотношением X = CY, где С = (cij) (i,j = 1,2,...,n) есть некоторая невырожденная матрица n-го порядка.
Тогда квадратичная форма
L = ХТАХ = (CY)ТA(CY) = (YТCТ)A(CY) = YТ(CТ AC)Y.
Итак,
при
невырожденном линейном преобразовании
X
= CY
матрица
квадратичной формы принимает вид:
![]() .
.
Пример 2. Дана квадратичная форма L(х1, х2) = 2x12 + 4x1x2 - 3x22. Найти квадратичную форму L(y1, y2), полученную из данной линейным преобразованием х1 = 2y1 – 3y2, x2 = y1 + y2.
Решение.
Матрица
данной квадратичной формы
![]() ,
а матрица линейного преобразования С
=
,
а матрица линейного преобразования С
=![]() .
.
Следовательно, матрицу искомой квадратичной формы находим по формуле:
 ,
,
Значит квадратичная форма имеет вид L(y1, y2) = 13y12 - 34у1у2 + 3у22. ►
Определение
4. Квадратичная
форма L
=![]() называется
канонической
(или
имеет канонический
вид), если
все ее коэффициенты аij
=
0 при i
j:
L
= a11x12
+ a22x22
+ ... + annxn2
=
называется
канонической
(или
имеет канонический
вид), если
все ее коэффициенты аij
=
0 при i
j:
L
= a11x12
+ a22x22
+ ... + annxn2
=
![]() ,а
ее матрица является диагональной.
,а
ее матрица является диагональной.
Справедлива следующая теорема.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Для всякой квадратичной формы существует такой базис, в котором она имеет канонический (и даже нормальный) вид.
Познакомимся с методами приведения квадратичной формы к каноническому виду: метод Лагранжа выделения полных квадратов и методом собственных векторов.
Пример
3.
Найти ортогональное преобразование,
приводящее квадратичную форму
![]() ,
заданную в евклидовом пространстве
,
заданную в евклидовом пространстве![]() ,
к каноническому виду. Написать этот
канонический вид.
,
к каноническому виду. Написать этот
канонический вид.
Решение:
матрица квадратичной формы имеет вид
 .
Найдем собственные числа этой матрицы:
.
Найдем собственные числа этой матрицы:![]() .
Соответственно ортонормированные
собственные векторы:
.
Соответственно ортонормированные
собственные векторы:

Следовательно,
в базисе из этих векторов, заданная
квадратичная форма имеет вид
 ,
,
где
соответствующие преобразования координат
имеют вид:
 ►
►
Канонический вид квадратичной формы не является однозначно определенным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные различными способами канонические формы обладают рядом общих свойств. Одно из этих свойств сформулируем в виде теоремы.
Теорема (закон инерции квадратичных форм). Число слагаемых с положительными (отрицательными) коэффициентами квадратичной формы не зависит от способа приведения формы к этому виду.
Следует отметить, что ранг матрицы квадратичной формы, называемый рангом квадратичной формы, равен числу отличных от нуля коэффициентов канонической формы и не меняется при линейных преобразованиях.
Лекция 17. Итоговое тестирование.
Лекция 18. Резерв.
Лекция 0. Входная контрольная работа за курс средней школы.
