2. Линейная зависимость системы векторов.

Определение 2.1. Выражение вида ₁а₁+₂а₂+...+_mа_m называется линейной комбинацией векторов а₁, а₂, ... а_m £, где ₁, ₂, ..., _m-1 — какие угодно действительные числа.

Определение 2.2. Векторы а₁, а₂, ..., а_m векторного пространства R называются линейно зависимыми, если существуют такие числа ₁, ₂, ..., _m, не равные одновременно нулю, что

₁а₁+₂а₂+...+_mа_m = 0, где 0 – ноль вектор.

В противном случае векторы а₁, а₂, ..., а_m называются линейно независимыми.

Примером линейно независимых векторов являются два не коллинеарных, т.е. не параллельных одной прямой, вектора а₁ и a₂ на плоскости. Действительно, условие ₁а₁+₂а₂ = 0 будет выполняться лишь в случае, когда ₁ = ₂ = 0, или если; например, ₂  0, то а₂ =а₁ и векторы a₁ и а₂ коллинеарны. Однако любые три вектора плоскости линейно зависимы.

Отметим некоторые свойства векторов линейного простран­ства.

1. Если среди векторов а₁, а₂, ..., а_m имеется нулевой вектор, то эти векторы линейно зависимы. В самом деле, если, например, e₁=0, то равенство ₁а₁+₂а₂+...+_mа_m = 0 справедливо при ₁ = 1, ₂ = .... = _m = 0.

2. Если часть векторов а₁, а₂, ..., а_m являются линейно зависи­мыми, то и все эти векторы - линейно зависимы. Действительно, если, например, векторы а₂, а₃, ..., а_m линейно зависимы, то спра­ведливо равенство ₂а₂+₃а₃+...+_mа_m = 0, в котором не все числа ₂, ₃, ..., _mравны нулю. Но тогда с теми же числам ₂, ₃, ..., _m, и ₁ = 0 будет справедливо равенство ₁а₁+₂а₂+...+_mа_m = 0

Пример 1. Выяснить, являются ли векторы а₁ = (1; 3; 1; 3),

а₂ = (2; 1; 1; 2) и а₃ = (3;-1;1;1) линейно зависимыми.

Решение. Составим векторное равенство ₁а₁ + ₂а₂ + ₃а₃ = 0. Записывая а₁, а₂, а₃ в виде вектор-столбцов, получим

Задача свелась, таким образом, к решению системы:

откуда найдем бесконечное множество ее решений ₁ = С, ₂ = -2С, ₃ = С), где С — произвольное действительное число.

Итак, для данных векторов условие ₁а₁ + ₂а₂ + ₃а₃ = 0 выполняется не толь­ко при ₁ = ₂ = ₃ = 0 (а, например, при ₁ = 1, ₂ = -2, ₃ = 1 (С = 1); при ₁ = 2, ₂ = -4, ₃ = 2 (С = 2) и т.д.), следовательно, эти векторы линейно зависимые.

Лекция 11. Базис и ранг системы векторов.

1. Базис и ранг системы векторов.

Определение 1.1. Линейное пространство R называется n-мерным, если в нем существует n линейно независимых векторов, а любые из (n +1) векторов уже являются зависимыми.

Другими словами, размерность пространства — это максимальное число содержа­щихся в нем линейно независимых векторов. Число n называется размерностью пространства R и обозначается dim(R).

Определение 1.2. Совокупность n линейно независимых векторов n-мерного пространства R называется базисом.

Справедлива следующая теорема.

Теорема. Каждый вектор х линейного пространства R можно представить и притом единственным способом в виде линейной комбинации векторов базиса.

x = x₁e₁ + x₂e₂ + ... + x_ne_n.

Это равенство называется разложением вектора х по базису е₁, е₂ ,..., е_n , а числа х₁,х₂,...,х_n — координатами вектора х отно­сительно этого базиса. В силу единственности разложения каждый вектор однозначно может быть определен координатами в некотором базисе.

Очевидно, что нулевой вектор имеет все нулевые координаты, а вектор, противоположный данному, — противоположные по знаку координаты.

Вывод: Базисом в линейном пространстве называется любая упорядоченная система векторов обладающая свойствами:

1. она линейно независима,

2. любой вектор из линейного пространства является линейной комбинацией векторов этой системы, т.е.

x = x₁e₁ + x₂e₂ + ... + x_ne_n.

Пример 1. В базисе е₁ , е₂, е₃ заданы векторы a₁ = (1; 1; 0), a₂ = (1;-1;1) и a₃=( -3; 5; -6). Показать, что векторы а₁, а₂, а₃ образуют базис. Разложить вектор а₄=(1;1;1) по этому базису.

Решение. Векторы a₁, а₂, а₃ образуют базис, если они ли­нейно независимы. Составим векторное равенство: ₁а₁ + ₂а₂ + ₃а₃ = 0.

⇒⇒

Система имеет единственном нулевом решение: ₁ = ₂ = ₃ = 0, т.е. векто­ры а₁, а₂, а₃ образуют систему линейно независимых векторов и, следовательно, составляют базис.

Разложение вектора по базису будет иметь вид: х₁а₁ + х₂а₂ + х₃а₃ = а₄. Тогда получаем систему уравнений:

⇒⇒⇒

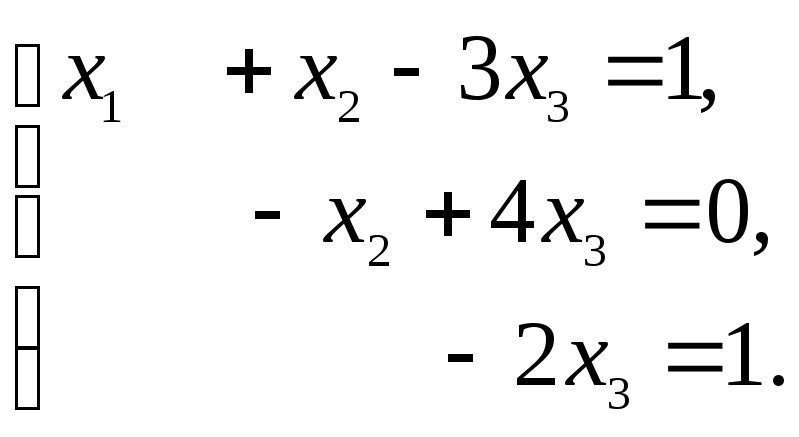Значит разложение вектора по данному базису а₁, а₂, а₃ будет иметь вид а₄=1,5а₁ - 2а₂ - 0,5а₃. Т.е. координаты вектора а₄ в базисе а₁, а₂, а₃ будут (1,5; -2; -0,5)

Утверждение 1. Всякая система векторов имеет хотя бы один базис; при этом оказывается, что все базисы этой системы имеют одинаковое количество векторов, называемое рангом системы векторов.

Другими словами, если множество обладает базисами, то все они состоят из одинакового числа векторов, называемого рангом. В частности, если все пространство £ имеет базис, то оно называется конечномерным и обозначается £_n, где n=dim£ - число векторов в любом базисе, называемое размерностью пространства. В противном случае пространство £ называется бесконечномерным.

Утверждение 2. Ранг всего пространства Rⁿ равен n и называется размерностью пространства; при этом в качестве базиса Rⁿ можно взять следующую систему:

е₁=(1;0;0;…,0), е₂=(0;1;0;…,0), е₃=(0;0;1;…,0), …, е_n=(0;0;0;…,1)

Этот базис принято называть каноническим.

2. Построение базиса системы векторов a₁, a₂, a₃,..., а_n и разложений векторов по базису.

Алгоритм решения задач:

1. Рассмотреть систему уравнений х₁а₁ + х₂а₂ + х₃а₃+…+х_n а_n=0 и найти равносильную ей разрешенную систему уравнений х₁а₁* + х₂а₂* + х₃а₃*+…+х_n а_n*=0.

2. Найти диагональную часть системы векторов a₁*, a₂*, a₃*,..., а_n*.

3. Отметить векторы системы a₁, a₂, a₃,..., а_n , соответствующие диагональной части системы a₁*, a₂*, a₃*,..., а_n*; они образуют базис системы a₁, a₂, a₃,..., а_n.

4. Разложить вектор а_j* по диагональной части системы a₁*, a₂*, a₃*,..., а_n*; он разлагается по базису найденному в пункте 3, с коэффициентами, которые совпадают с коэффициентами разложения а_j* по диагональной части системы a₁*, a₂*, a₃*,..., а_n*.

Пример 2. Найти базис системы векторов и векторы не входящие в базис, разложить по базису: a₁ = (5; 2; -3;1), a₂ = (4;1;-2;3), a₃=( 1; 1; -1;-2), a₄ = (3; 4; -1;2), a₅ = (13;8;-7;4) и a₃=( -3; 5; -6).

Решение. Рассмотрим систему линейных уравнений х₁а₁ + х₂а₂ + х₃а₃+ х₄а₄ + х₅а₅ =0 и методом Гаусса найдём разрешенную систему уравнений:

Шаг 1 x1 x2 x3 x4 x5 5 4 1 3 13 2 1 1 4 8 -3 -2 -1 -1 -7 1 3 -2 2 4	Шаг 2 x1 x2 x3 x4 x5 5 4 1 3 13 -3 -3 0 1 -5 2 2 0 2 6 11 11 0 8 30
Шаг 3 x1 x2 x3 x4 x5 0 -1 1 -2 -2 0 0 0 4 4 1 1 0 1 3 0 0 0 -3 -3	Шаг 4 x1 x2 x3 x4 x5 0 -1 1 0 0 0 0 0 1 1 1 1 0 0 2 0 0 0 0 0

Разрешённая система уравнений, равносильная исходной, имеет вид х₁а₁* + х₂а₂* + х₃а₃*+ х₄а₄* + х₅а₅*=0, где

, ,,,.

Векторы а₁*, а₃*, а₄* образуют диагональную систему. Следовательно, векторы а₁, а₃, а₄ - базис системы векторов a₁, a₂, a₃, a₄, a₅.

Разложим теперь векторы а₂ и а₅ по базису а₁, а₃, а₄. Для этого сначала разложим соответствующие векторы а₂* и а₅* по диагональной системе а₁*, а₃*, а₄*, имея в виду, что коэффициентами разложения вектора по диагональной системе являются его координаты:

а₂*= а₁*- а₃*+0 а₄*,

а₅*=2а₁*+0а₃*+ а₄*.

Векторы а₂ и а₅ разлагаются по базису а₁, а₃, а₄ с теми же коэффициентами, что и векторы а₂* и а₅* по диагональной системе а₁*, а₃*, а₄*:

а₂= а₁- а₃+0 а₄,

а₅=2а₁+0а₃+ а₄.

Задача решена.

Пример 3. Найти размерность и базис линейного подпространства, являющегося линейной оболочкой векторов. Записать разложение векторов системы по найденному базису.

,

.

Решение. Составим из координатных столбцов векторов системы матрицу и с помощью элементарных преобразований определим ее ранг. Ранг этой матрицы будет совпадать с числом линейно независимых векторов в системе и значит, равен размерности оболочки векторов. Матрица из координатных столбцов имеет вид:

Умножим элементы первого столбца на –2 и прибавим к соответствующим элементам второго и пятого столбцов, затем элементы первого столбца умножим на –1 и прибавим к соответствующим элементам третьего и четвертого столбцов. В результате получим матрицу эквивалентную исходной, она будет иметь вид:

Вычитая теперь из третьего столбца второй, а из пятого – четвертый получаем опять матрицу, которая эквивалентна исходной:

.

Таким образом, ранг этой матрицы равен трем и размерность линейной оболочки тоже будет равна трем. В качестве базиса можно взять векторы (вектор является линейной комбинацией векторов и поэтому не может быть базисным).

Находим разложение векторов системы по этому базису. Пусть

,

что равносильно системе линейных алгебраических уравнений (СЛАУ)

,

решая которую, находим , т.е..

Записывая разложение вектора и решая аналогичную систему, находим.

Пример 4. Найти базис ортогонального дополнения линейной оболочки системы векторов, заданных в некотором ортонормированном базисе четырехмерного евклидова пространства :

Решение. Запишем систему, используя координаты векторов и найдем ее фундаментальную систему решений

.

~ ~.

Из последних двух уравнений получаем:

Пусть х₃=1 и х₄=0, тогда

Пусть х₃=0 и х₄=1, тогда .

Таким образом, базисом линейной оболочки системы векторов являются векторы

.

Лекция 12. Пространства со скалярным произведением. Евклидовы пространства.