
1. Определение линейного оператора
Одно из фундаментальных понятий матричной алгебры — понятие линейного оператора.
Рассмотрим два линейных пространства: Rn размерности n и Rm размерности m.
Определение 1. Если задан закон (правило), по которому каждому вектору х пространства Rn ставится в соответствие единственный вектор у пространства Rm, то говорят, что задан оператор (преобразование, отображение) А(х), действующий из Rn в Rm, и записывают у = А (х).
Определение 2. Оператор (преобразование) называется линейным, если для любых векторов х и у пространства Rn и любого числа выполняются соотношения:
А(х + у) = А(х) + А(у) — свойство аддитивности оператора;
А(х) = А(x) — свойство однородности оператора.
Определение 3. Вектор у = А(х) называется образом вектора x, а сам вектор х — прообразом вектора у.
Если пространства Rn и Rm совпадают, то оператор А отображает пространство Rn в себя. Именно такие операторы мы будем рассматривать в дальнейшем.
Связь между вектором х и его образом у = А(х) можно выразить в матричной форме уравнением
Y = А∙Х,
где А — матрица линейного оператора, X = (х1,х2,...,хn)Т,
Y = (y1, y2,..., yn)Т - матрицы-столбцы из координат векторов х и у.
Пример
1.
Пусть
![]() Являются ли линейными следующие
преобразования?
Являются ли линейными следующие
преобразования?
![]()
![]()
Решение.
Преобразование
будет линейным, если все координаты
образов векторов будут линейными
комбинациями координат вектора
![]() .
Здесь в преобразовании
.
Здесь в преобразовании![]() вторая координата равная
вторая координата равная![]() не является линейной комбинацией, в
преобразовании
не является линейной комбинацией, в
преобразовании![]() ,
аналогично, кроме того, третья координата
имеет вид
,
аналогично, кроме того, третья координата
имеет вид![]() ,
что так же не является линейной комбинацией
координат вектора
,
что так же не является линейной комбинацией
координат вектора![]() .
Значит, эти преобразования не являются
линейными. Преобразование
.
Значит, эти преобразования не являются
линейными. Преобразование![]() является линейным.
является линейным.
Пример 2. Пусть в пространстве R3 линейный оператор А,
в
базисе е1,
е2,
е 3
задан
матрицей A
=
 .
.
Найти образ у = А(х) вектора х = 4е1 - Зе2 + е3.
Решение. По формуле Y = А∙Х имеем

Следовательно, у = 10el - 13e2 - 18е3. ►
2. Действия над линейными операторами.
Определение 4. Суммой двух линейных операторов А и В называется оператор (А + В), определяемый равенством: (А + В)(х) = А(х) + В(х).
Определение 5. Произведением линейного оператора А на число называется оператор А , определяемый равенством (А)(х) = (А(х)).
Определение 6. Произведением линейных операторов А и В называется оператор АВ, определяемый равенством: (АВ)(х) = А(В(х)).
Можно убедиться в том, что операторы (А + В), А, АВ полученные в результате этих действий, удовлетворяют отмеченным выше свойствам аддитивности и однородности, т.е. являются линейными.
Определим нулевой оператор О, переводящий все векторы пространства Rn в нулевые векторы 0(х) = 0, и тождественный оператор Е, действующий по правилу: Е(х) = х.
Пример 3. Выяснить, какие из заданных отображений в себя пространства арифметических векторов R3 являются линейными операторами. Выписать их матрицы в каноническом базисе:
А(х)=(х1, х2+1, х3+2) – не является линейным оператором;
А(х)=(х2 +х3 ,2х1 +х2 , 3х1 – х2 +х3) – является линейным оператором с матрицей
 .
.
Пример 3. В пространстве заданы два линейных оператора А и В. Найти матрицу С линейного оператора С=АВ и его явный вид в каноническом базисе:
А(х)=(2х2, -2х1 +3х2 +2х3 , 4х1 – х2 +5х3 ), В(х)=(-3х1 +х3 , 2х2 +х3 , -х2 +3х3 ).
Решение:
Составим матрицы операторов
 .С=АВ=
.С=АВ= .
.
Следовательно С(х) =(4х2 +2х3, 6х1 +4х2 +7х3 , -12х1 -7х2 +18х3 ).
Пример 4. Пусть
![]()
Найти
ψ(х)=![]()
Решение.
Матрицы
преобразований
![]() будут соответственно
будут соответственно
 .
Пусть
.
Пусть
![]() – матрица преобразования
– матрица преобразования![]() ,
тогда
,
тогда

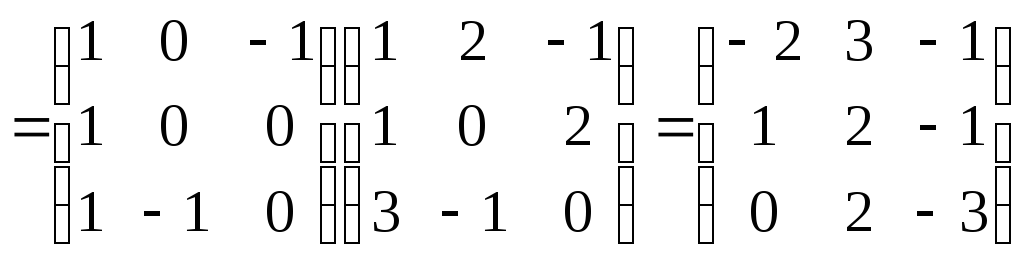 .
.
![]() .
.
