1. Решение произвольных систем уравнений. Метод Гаусса.

Пусть задана система m линейных уравнений с n неизвестными:

(1)

Рассмотрим один из самых простых методов решения систем уравнений, заключающийся в последовательном исключении неизвестных и называемый методом Гаусса. Данный метод заключается в том, что с помощью элементарных преобразований строк расширенной матрицы системы уравнений, она приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних по номеру переменных, находятся все остальные. Метод Гаусса имеет ряд преимуществ:

1. значительно менее трудоёмкий;

2. позволяет однозначно установить, совместна система или нет, а в случае её совместности найти её решения (единственное или бесконечное множество);

3. дает возможность определить ранг матрицы системы.

С помощью элементарных преобразований над строками приведем расширенную матрицу системы (2.1) (А|В) к ступенчатому виду (А`|Н`):

,

где при.

Полученной расширенной матрице (А`|Н`) соответствует система линейных уравнений, эквивалентная системе (2.1). При этом r(A) = r(A`), r(A`|Н`) = r(A|Н), и утверждения о том, что полученная система совместна (несовместна) и определена (неопределенна) верны и для системы (2.1).

Если хотя бы одно из чисел отлично от нуля, то система линейных уравнений несовместна.

Если же , то система совместна, ее ранг равенr. Очевидно, что минор, стоящий на пересечении первых r строк и r столбцов, не равен нулю, следовательно, его можно принять за базисный. Назовем переменные базисными, а- свободными. Отбрасывая строки с нулевыми элементами, получаем систему изr уравнений:

(1)

Если r = n , то матрица этой системы треугольная, все переменные – базисные, и их значения определяются однозначно.

Если r < n, то из системы легко выразить базисные переменные через свободные переменные. Придавая свободным переменным произвольные значения:

,

последовательно получаем выражения для базисных переменных

.

Определение . Решение, задаваемое формулами

где - любые действительные числа, называетсяобщим решением системы (2.1).

Пример 1. Решить методом Гаусса систему уравнений

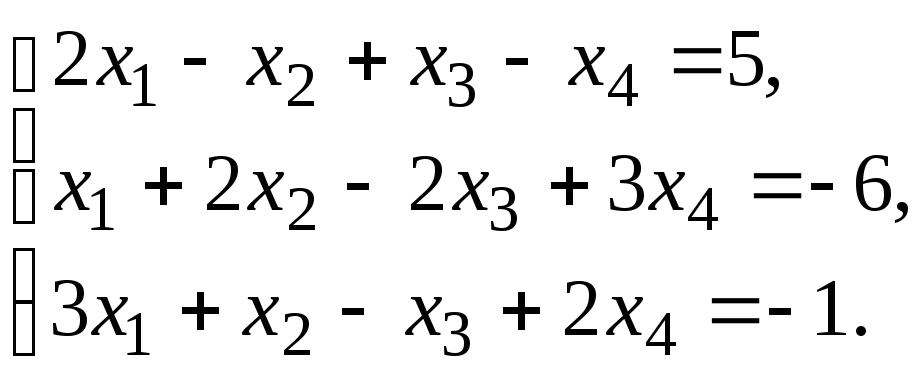
Составим расширенную матрицу и с помощью элементарных преобразований приведем ее к ступенчатому виду

.

r(A) = r(A|Н) = 2 < 4, следовательно, система имеет бесконечное множество решений.

Исходная система равносильна системе:

Решим ее.

, этот минор можно принять за базисный. Тогда, x₁, x₂ – базисные переменные, а остальные x₃, x₄ – свободные переменные.

Задавая свободным переменным произвольные значения x₃ = c₁, x₄ = c₂ найдем бесконечное множество решений.

Ответ:

Второй способ применения метода Гаусса.

Применение метода Гаусса для решения систем линейных уравнений заключается в последовательном исключении неизвестных в уравнениях системы (6.1) с целью приведения ее к треугольному виду:

(2)

При этом допускаются следующие элементарные преобразования системы, приводящие к эквивалентным системам уравнений:

а) перестановка уравнений в системе;

б) умножение обеих частей уравнений на одно и то же число неравное нулю;

в) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на одно и то же число;

г) исключение уравнений вида 0 = 0.

В полученной системе (2) вычисляется из 3-го уравнения и его значение подставляется во 2-е уравнение, затем из 2-го уравнения вычисляетсяи подставляется вместе св 1-ое уравнение, после чего из 1-го уравнения вычисляется.

Пример 2. Дана система линейных уравнений .

Решить методом Гаусса.

Решение: Применим метод Гаусса к решению данной системы.

ШАГ 1: умножим 1-ое уравнение системы на 1/ 2, чтобы коэффициент при x₁ стал равен единице

ШАГ 2: члены первого уравнения, во-первых, умножим на (-3)

и прибавим к членам второго уравнения, во-вторых, умножим на

(-5) и прибавим к членам третьего уравнения. В результате

получим систему:

ШАГ 3: к членам третьего уравнения прибавим члены второго уравнения.В результате получим:

Таким образом, исходная система приведена к эквивалентной системе треугольного вида. Как известно, она имеет единственное решение. Решаем эту систему, начиная с последнего уравнения:

Следовательно, решение системы:

Пример 3. Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом ис­пользуется сырье трех типов: S_l, S₂, S₃. Нормы расхода каждого из них на одну пару обуви и объем расхода сырья на 1 день зада­ны таблицей:

Вид сырья	Нормы расхода сырья на одну пару, усл.ед.			Расход сырья на 1 день,
	Сапоги	Кроссовки	Ботинки
S1	5	3	4	2700
S2	2	1	1	900
S3	3	2	2	1600

Найти ежедневный объем выпуска каждого вида обуви.

Решение. Пусть ежедневно фабрика выпускает х пар са­пог, y пар кроссовок и z пар ботинок. Тогда в соответствии с расходом сырья каждого вида имеем систему:

Решая систему любым способом, находим x = 200, y = 300, z = 200, т.е. фабрика выпускает 200 пар сапог, 300 — кроссовок и 200 пар ботинок. Рассмотрим, например, решение системы методом Гаусса:

Ответ: ежедневный объем выпуска каждого вида обуви составляет 200 пар сапог, 300 пар кроссовок и 200 пар ботинок.

Лекция 9. Системы линейных однородных уравнений.