Алгоритм вычисления обратной матрицы методом элементарных преобразований (метод Гаусса)

1. Приписываем справа к матрице А размера единичную матрицу того же размера, получим прямоугольную матрицуразмера.

2. С помощью элементарных преобразований над строками матрицы Г сначала приведем ее к ступенчатому виду , где матрица А₁ – треугольная.

3. Затем, так же, с помощью элементарных преобразований приведем Г₁ к виду .

Пример 2. Найти матрицу, обратную к данной методом Гаусса:

1. .

2. .

3. .

2. Ранг матрицы. Совместность систем.

Пусть задана система m линейных уравнений с n неизвестными:

(1)

Определение 4. Если , то система (1) называетсяоднородной. Если же хотя бы одно из этих чисел отлично от нуля, то система неоднородная.

Для исследования данной системы составим матрицу из коэффициентов при неизвестных. Для решения многих задач важное значение имеет понятие ранга матрицы.

Определение 5. В матрице A_mn вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы k-го порядка, где kmin(m;n). Определители таких матриц называются минорами k-го порядка матрицы A_mn.

Определение 6. Рангом матрицы A_mn называется наивысший порядок ненулевых миноров этой матрицы.

Обозначается rang A или r(A).

Из определения следует:

1. ранг матрицы A_mn не превосходит меньшего из её размеров;

2. r(A) = 0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А нулевая матрица.

3. Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А имеет определитель отличный от нуля.

Определение 7. Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.

Пример 2. Вычислить ранг матрицы и указать какой-либо ее базисный минор.

Решение: матрица имеет четвертый порядок, но detА = 0. Все миноры 3-го порядка тоже равны нулю, так как содержат хотя бы один нулевой столбец (свойство 5⁰ определителя). Все миноры 2-го порядка тоже равны нулю, тек как содержат либо нулевой столбец, либо пропорциональные столбцы (свойство 6⁰). Значит r(A) = 1, т.к. есть элементы отличные от нуля. Любой такой элемент можно принять за базисный минор, к примеру, .

Пример 3. Вычислить ранг матрицы и указать какой-либо ее базисный минор.

Решение: А_34 значит r(A)  3. Среди миноров третьего порядка лишь один не содержит нулевого столбца. Вычислим его:

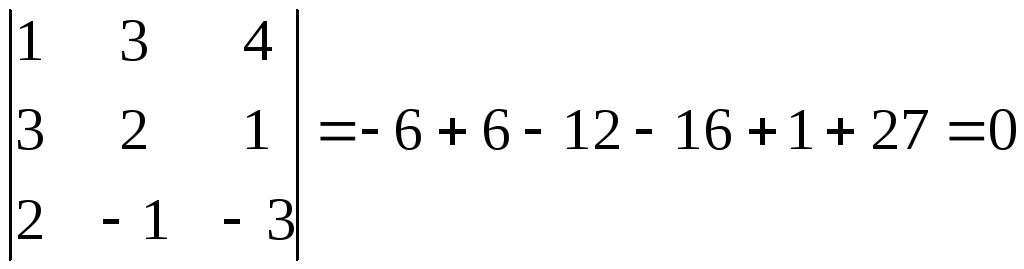
Итак, все миноры третьего порядка равны нулю. Среди миноров второго порядка есть ненулевые, например, . Следовательно,r(A) = 2.

Для облегчения нахождения ранга матрицы используются элементарные преобразования матриц, которые сохраняют её ранг. Напомним, что к элементарным преобразованиям матриц относятся:

1) Умножение всех элементов строк или столбцов матрицы на число, отличное от нуля.

2) Изменение порядка строк или столбцов матрицы.

3) Прибавление к каждому элементу одной строки или столбца соответствующих элементов другой строки или столбца, умноженных на любое число.

С помощью элементарных преобразований строк и перестановки столбцов можно привести матрицу к трапециевидному или ступенчатому виду, когда определение её ранга не составляет труда.

Определение 8. Трапециевидной или ступенчатой называется матрица вида:

,

где

Ранг трапециевидной или ступенчатой матрицы равен количеству ненулевых строк.

Пример 4. Найти ранг матрицы

Лекция 5. Матричные уравнения. Системы линейных уравнений.