1. Системы линейных уравнений с квадратной невырожденной матрицей

В случае системы линейных уравнений с квадратной невырожденной матрицей возможно также решение средствами матричного исчисления.

Пусть число уравнений системы равно числу перемен­ных, т.е.

(1)

Тогда матрица системы является квадратной, а ее определитель  = |A| называется определителем системы. Запишем систему вида (1) в матричном виде, обозначив матрицу коэффициентов при неизвестных , матрицу столбец свободных членов, матрицу столбец неизвестных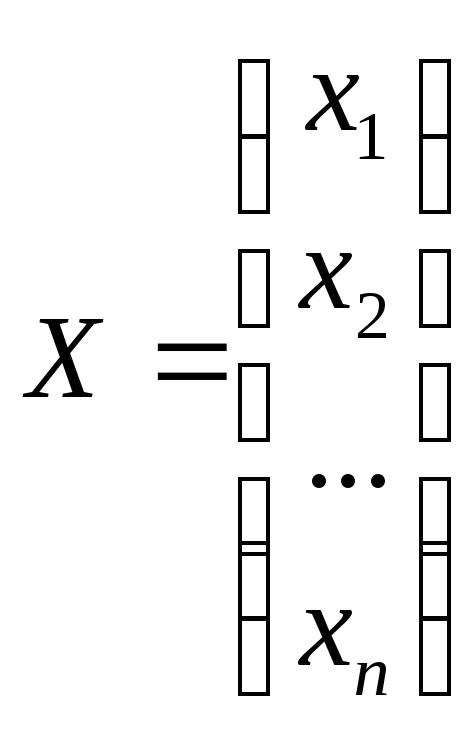. Умножая матрицы АХ, получаем новую матрицу, элементами которой являются левые части уравнений системы (1). На основании равенства матриц систему (1) можно записать систему (1) в виде АХ=В.

Предположим, что матрица системы А невырожденная, т.е. ее определитель отличен от нуля. Тогда существует обратная матрица А^-1. Следовательно решение системы (1) имеет вид Х = А^-1 В. Т.е., чтобы найти решение системы, нужно обратную матрицу умножить на столбец свободных членов справа.

Пример 1. Дана система линейных уравнений

.

Доказать ее совместность и решить средствами матричного исчисления.

РЕШЕНИЕ

Докажем совместность. Запишем расширенную матрицу системы

и найдем ее ранг. Элемент матрицы , стоящий в левом верхнем углу,отличен от нуля, следовательносреди миноров второго порядка, окаймляющих (включающих в себя) этот элемент, также есть отличные от нуля, например,

, т.е. .

Из миноров третьего порядка, окаймляющих , возьмем минор

:

Т.к. то, а т.к. у матрицыминоров 4-го порядка не существует, то. Так как , то и . Таким образом, , и совместность доказана.

1. Применяем матричный метод к решению системы. Формируем матрицы, состоящие из элементов системы:

а) Определитель системы , значит, матричный метод применим.

б) Запишем систему в матричном виде :

в) Вычисляем алгебраические дополнения .

Подставляя найденные значения в формулу (6.3), получим:

г) воспользуемся формулой (6.4).

получим:

Итак, решение системы:

Пример 2. Решить систему уравнений матричным методом.

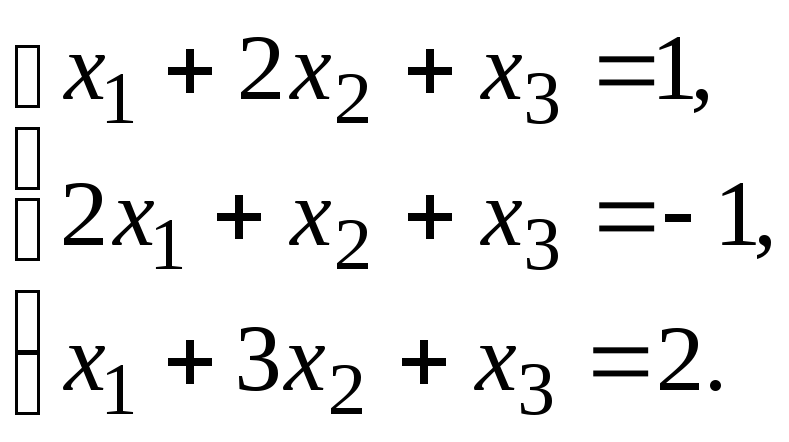
Решение:

Находим обратную матрицу (самостоятельно)

. Следовательно, по формуле Х = А^-1Н, получаем ,

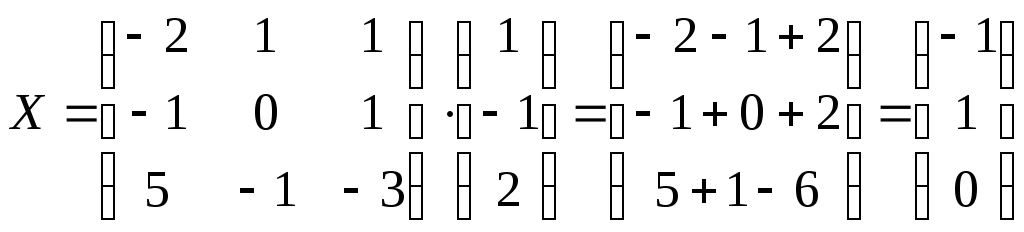т.е.

Ответ:

Лекция 7. Решение систем линейных уравнений по формулам Крамера.

1. Решение систем по формулам Крамера.

Рассмотрим решение системы двух уравнений с двумя пере­менными:

(3) в которой хотя бы один из коэффициентов при переменных от­личен от нуля.

Для решения этой системы исключим переменную х₂, умно­жив первое уравнение на a₂₂, второе — на (-a₁₂) и сложив их. Затем исключим переменную х₁, умножив первое уравнение на (-a₂₁ ), второе — на a₁₁ и также сложив их. В результате получим систему:

Выражение в скобках есть определитель системы

Обозначив система примет вид: Из полученной системы следует, что если определитель сис­темы  = 0, то система имеет единственное решение, определяемое по формулам:

Если  = 0, a ₁ 0 (или ₂  0), то система (3) несовместная, так как в этом случае приводится к виду:

Если  = ₁ = ₂ = 0 , то система (2) неопределенная и имеет бесконечное множество решений, так как в этом случае приводится к виду:

Для получения решения системы (2) в общем виде предположим, что квадратная матрица системы А_nn невырож­денная, т.е. ее определитель |A|  0. В этом случае существует обратная матрица А^-1.

Умножая слева обе части матричного равенства на матри­цу А^-1, получим A^-1(AX)=A^-1 В. Так как A^-1(AX)=(A^-1A)B= ЕХ = X , то

Теорема Крамера. Пусть  — определитель матрицы системы A, a j — определитель матрицы, получаемой из матрицы А заме­ной j-го столбца столбцом свободных членов. Тогда, если   0, то система имеет единственное решение, определяемое по формулам:

Эти формулы получили название формул Крамера.

Доказательство: решением системы методом обратной матрицы будет матрица-столбец X=A^-1B. Обратная матрица A^-1= , где A^* — матрица, присоединенная к матрице А. Так как элементы матрицы А^* есть алгебраические дополнения элементов матрицы А^T , транспонированной к А, то запишем данное равенство в раз­вернутой форме:

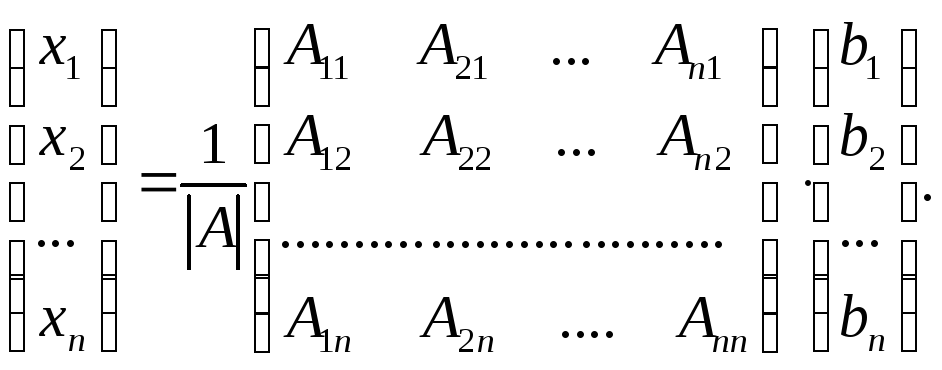Учитывая, что , получим после умножения матриц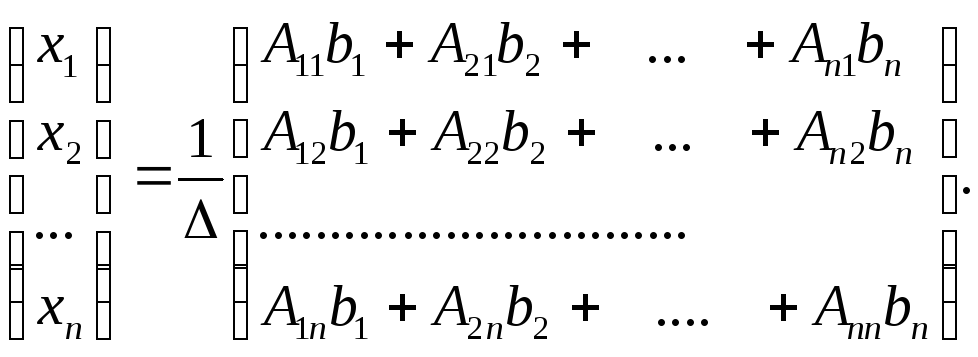Откуда следует, что для любогоj (j = 1,2,3,4,...,n) .

На основании свойств определителей , где_j – определитель матрицы, полученной из матрицы А заменой j-го столбца столбцом свободных членов. Следовательно, .(j = 1,2,3,4,....n) , т.е.

Пример 1. Решить систему уравнений по формулам Крамера.

Решение. Найдем определитель системы  = |А| = 5 . Так как   0, то по теореме Крамера система имеет единственное реше­ние.

Вычислим определители матриц ₁, ₂, ₃, полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:

Теперь по формулам Крамера получаем т.е. решение системы (4; 2; 1).

В конце решения системы (любым способом) рекомендуем сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства.

Пример 2. Решить систему по формулам Крамера.

Решение. Составим

Вычислим определитель этой системы:

.

Последовательно заменяя в определителе ∆ первый, второй и третий столбцы столбцом свободных членов, получим:

, , .

Подставим значения определителей в формулы Крамера.

Ответ:

Существенным недостатком решения систем n линейных уравнений с n переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных экономических задач, сводящихся часто к системам с большим числом уравнений и переменных.

Лекция 8. Общее решение систем линейных уравнений.