23

Глава 15. Определённый интеграл

§15.1.Понятие площади плоской фигуры. Задача о вычислении площади криволинейной трапеции

15.1.1. Площадь многоугольника

Начнём изложение теории определённого интеграла с постановки актуальной задачи о вычислении площади плоской фигуры, ограниченной кривыми линиями. К этой задаче сводятся многие математические модели, в том числе модели экономических теорий. Для решения задачи о площади, а также многих других важных задач, в этой главе излагается теория определённого интеграла.

Поставим перед собой вопрос, а что же такое площадь фигуры, которую мы собираемся вычислять? На память сначала придут известные из школьного курса формулы для вычисления площадей различных фигур – прямоугольника, треугольника, других многоугольников. Отметим, что понятие площади многоугольника является достаточно очевидным, оно не вызывает вопроса, как его определить. Однако если обратиться к понятию площади даже такой простой фигуры, как круг, то его в школьном курсе определяли уже с помощью предельного перехода, рассматривая последовательность площадей вписанных в круг многоугольников. Таким образом, для каких-то фигур, например, многоугольников, понятие площади является интуитивно ясным. Площади других фигур будем определять, приближая эти фигуры многоугольниками.

Этот подход вполне практичен. Для приближённого, нахождения площади какой- то фигуры, например, участка на карте, часто используется следующий приём. Участок карты накрывается сеткой, состоящей из квадратов определённой площади. Считают, сколько квадратов целиком содержится в измеряемой фигуре и в скольких квадратах эта фигура расположена хотя бы частично. Эти два числа дают границы, в которых находится интересующая нас площадь. Если полученная точность измерения недостаточна, то следует взять более мелкую сетку.

Изложенные выше соображения послужат нам для более строгого определения понятия площади. Отправной точкой считаем понятие площади треугольника, которое предполагаем известным.

Для того, чтобы определить площадь произвольного многоугольника, разобьём его на треугольники, вычислим площади этих треугольников и просуммируем их.

Следует доказать корректность этого определения. Это означает, что:

если разбить многоугольник на треугольники каким-то другим способом и просуммировать площади вновь полученных треугольников, то в результате получится то же самое число.

► Возьмем два разбиения некоторого многоугольника на треугольники. Построим общее разбиение, взяв разделяющие линии этих двух разбиений. В результате получится разбиение исходного многоугольника на более мелкие многоугольники. Те мелкие многоугольники, которые не являются треугольниками, разобьём на треугольники.

Тогда площади частей как 1-го, так и 2-го разбиения получаются, как суммы площадей маленьких треугольников из результирующего разбиения. Поэтому суммы площадей треугольников - частей 1-го и 2-го разбиения отличаются друг от друга только порядком и их величины одинаковы.◄

Площадь многоугольника обозначим .Она обладает такими свойствами:

1. Площадь любого многоугольника неотрицательна;

1. Если ,- многоугольники, то

пл. () = пл. () + пл. () - пл. (),

в частности, если пл. () = 0 то

пл. () = пл. () + пл. ().

Это свойство называется аддитивностью площади. Из него следует, что если , то пл. ()пл. ().

15.1.2. Площадь плоской фигуры.

Пусть теперь - ограниченная плоская фигура. Рассмотрим множество {} многоугольников таких, чтои множество {} многоугольников таких, что. Множество площадей {пл. ()}многоугольниковограничено сверху площадью любого многоугольникатакого, что. Поэтому существует точная верхняя грань этого числового множества,.

Аналогично, для множества площадей {пл. ()}многоугольников,, существует точная нижняя грань.

Определение. Плоская фигура называется имеющей площадь (квадрируемым множеством), если:

при этом общее значение этих величин называется её площадью

Нетрудно заметить, что:

1. Площадь любой квадрируемой фигуры P неотрицательна.

►По определению а все◄

2. Аддитивность площади, т.е. равенство пл.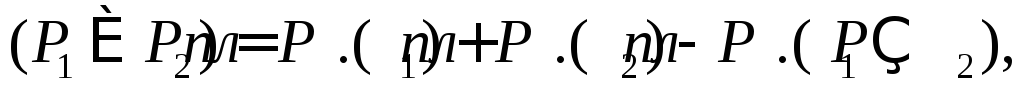также имеет место для квадрируемых фигур

►Достаточно доказать это равенство в случае, когда пл.

Пусть Выберем многоугольникитак, чтобыТогдаиоткудат.е. Следовательно, .

Поэтому:

Ввиду произвольности числа это означает, чтоимеет площадь, ичто и требовалось доказать. ◄

Иногда оказывается полезным такое утверждение.

Теорема 15.1. Пусть - плоская фигура, множество квадрируемых фигур - множество квадрируемых фигур

Если то - квадрируемая фигура, причем её площадь равна общему значению этих величин.

►Для доказательства достаточно для произвольного выбрать сначала квадрируемые фигурытак, чтобыи. Затем выберем многоугольники так, что тогда

Таким образом, для фигуры можно выбрать многоугольники так, что и площади и столь угодно близки, что и означает квадрируемость .◄

Вернёмся к поставленной задаче нахождения площади фигуры, ограниченной кривыми линиями. Например, рассмотрим фигуру, ограниченную снизу осью , по бокам — отрезками вертикальных прямыхи,, а сверху — графиком непрерывной на отрезкефункции(см. рис.)

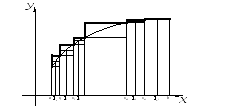
Разобьём отрезок на части и рассмотрим площадь ступенчатой фигуры, ограниченной сверху соответствующей этому разбиению полужирной линией, целиком лежащей под графиком функции. Рассмотрим также площадь ступенчатой фигуры, ограниченной сверху жирной линией и целиком лежащей над графиком функции. Площади этих ступенчатых фигур – многоугольников – при условии, что мы берём всё более мелкие отрезки, становятся всё ближе. То значение, к которому эти площади приближаются, и есть искомая площадь.

На первый взгляд кажется, что поставленная в начале параграфа задача решена. Получен алгоритм вычисления площади с заданной точностью. Однако

в этом алгоритме нет никакой математической хитрости и применение его на практике было бы долгим занятием. Поэтому переходим к следующему параграфу!