
- •Глава 10. Дифференциальное исчисление функций нескольких переменных
- •§10.1. Дифференцируемость функции многих переменных
- •10.1.1.Определение дифференцируемости функции многих переменных. Частные производные
- •10.1.2. Достаточное условие дифференцируемости функции нескольких переменных
- •§10.2. Дифференциал функции многих переменных и дифференциал отображения
- •10.2.1. Дифференциал функции многих переменных
- •10.2.2 Дифференциал отображения
- •§10.3. Производная сложной функции. Инвариантность формы первого дифференциала. Свойства матрицы Якоби
- •10.3.1. Производная сложной функции
- •10.3.2. Инвариантность формы первого дифференциала
- •10.3.3. Свойства матрицы Якоби. Якобиан
- •§10.4.Геометрические приложения
- •10.4.1. Касательная плоскость
- •10.4.2. Производная по направлению, градиент
- •§10.5.Производные и дифференциалы высших порядков
- •10.5.1. Производные высших порядков
- •10.5.2. Дифференциалы высших порядков
- •10.5.3.Второй дифференциал функции. Матрица Гессе
Глава 10. Дифференциальное исчисление функций нескольких переменных
§10.1. Дифференцируемость функции многих переменных
10.1.1.Определение дифференцируемости функции многих переменных. Частные производные
Пусть
![]() определена в некоторой окрестности
точки
определена в некоторой окрестности
точки![]() ,
,![]() - точка из этой окрестности.
- точка из этой окрестности.
Определение.
Величина
![]() называетсяприращением
функции
называетсяприращением
функции
![]() в точке,
в точке,![]() соответствующим приращению аргумента
соответствующим приращению аргумента![]() .
.
Определение.
Функция
![]() называетсядифференцируемой
в точке
называетсядифференцируемой
в точке
![]() ,
если существуют такие постоянные числа
,
если существуют такие постоянные числа![]() и функции
и функции![]() при
при![]()
![]() (1)
(1)
Часто обозначают
![]() и
и![]() .
Тогда (1) перепишем в виде
.
Тогда (1) перепишем в виде![]() .
.
При
![]() наше определение (1) совпадает с известным
определением дифференцируемости
наше определение (1) совпадает с известным
определением дифференцируемости![]() (пункт 6.1.1). Для функций одной переменной
дифференцируемость равносильна
существованию производной( теоремы 6.2
и 6.3). В случае нескольких переменных
ситуация несколько сложнее.
(пункт 6.1.1). Для функций одной переменной
дифференцируемость равносильна
существованию производной( теоремы 6.2
и 6.3). В случае нескольких переменных
ситуация несколько сложнее.
Сначала введем в
рассмотрение величину
![]() .
Она представляет собой приращение
функции при фиксированных значениях
всех производных, кромеi-той.
.
Она представляет собой приращение
функции при фиксированных значениях
всех производных, кромеi-той.
Пусть
![]() дифференцируема в точке
дифференцируема в точке![]() .
Тогда для любого
.
Тогда для любого![]() равенство (1) дает
равенство (1) дает
![]() при
при
![]() (2)
(2)
Поскольку
![]() при фиксированных значениях
при фиксированных значениях![]() равносильно тому, что
равносильно тому, что![]() ,
равенство (2) означает, что функция
,
равенство (2) означает, что функция![]() одной переменной
одной переменной![]() дифференцируема в точке
дифференцируема в точке![]() и, значит, существует предел
и, значит, существует предел![]()
![]() (3)
называемый, по определению,
частной
производной функции
(3)
называемый, по определению,
частной
производной функции
![]() по переменной
по переменной![]() в точке
в точке![]() .
.
Мы только что, тем самым, доказали теорему:
Теорема 10.1.
Если
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то для всех
,
то для всех![]() существуют
существуют![]() .
.
Таким образом, существование частных производных – необходимое условие дифференцируемости. При этом
![]()
![]() при
при
![]() .
.
Другое необходимое условие дифференцируемости – непрерывность функции, как показывает следующая теорема.
Теорема 10.2.
Если
![]() дифференцируема в точке
дифференцируема в точке![]() ,
то
,
то![]() .
.
►Достаточно
доказать, что при
![]() ,
,![]() ,
(т.к.
,
(т.к.![]() ).
Но это сразу следует из равенства (1),
так как
).
Но это сразу следует из равенства (1),
так как![]() .
◄
.
◄
Однако, в отличие
от случая
![]() ,
из существования частных производных
,
из существования частных производных![]() ,определенных
равенством (3) не следует даже непрерывность
функции
,определенных
равенством (3) не следует даже непрерывность
функции![]() в точке
в точке![]() и тем более не следует дифференцируемость
и тем более не следует дифференцируемость![]() в точке
в точке![]() ,
согласно теореме10.2.
,
согласно теореме10.2.
Пример.
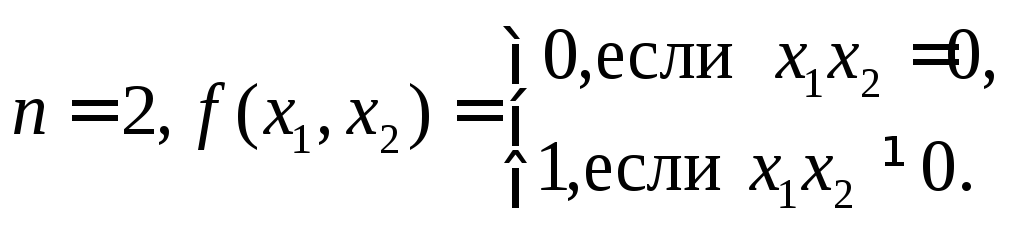 Тогда
Тогда
![]() ,
так как
,
так как![]() .
Аналогично,
.
Аналогично,![]() .
Однако
.
Однако![]() даже не непрерывна в точке
даже не непрерывна в точке![]() .
.
10.1.2. Достаточное условие дифференцируемости функции нескольких переменных
Достаточное условие дифференцируемости дает следующая теорема.
Теорема 10.3.
Пусть частные
производные
![]() существуют в окрестности точки
существуют в окрестности точки![]() и непрерывны в этой точке. Тогда
и непрерывны в этой точке. Тогда![]() дифференцируема в точке
дифференцируема в точке![]() .
.
► Рассмотрим
сначала простой случай
![]() .
.
Пусть точки
![]() и
и![]() принадлежат рассматриваемой окрестности
принадлежат рассматриваемой окрестности![]() точки
точки![]() .
Рассмотрим приращение функции в точке
.
Рассмотрим приращение функции в точке![]() :
:![]() и представим его в виде:
и представим его в виде:
![]() .
.
Зафиксировав
![]() ,
рассмотрим функцию от переменной
,
рассмотрим функцию от переменной![]() вида
вида
![]() .
.
Поскольку в
![]() существуют частные производные, функция
существуют частные производные, функция![]() дифференцируема на любом промежутке,
содержащем
дифференцируема на любом промежутке,
содержащем![]() и
и![]() .
Применим поэтому теорему Лагранжа,
согласно которой
.
Применим поэтому теорему Лагранжа,
согласно которой
![]() ,
где
,
где
![]() .
.
По определению частной производной,
![]() .
.
Поэтому
![]() .
.
Аналогичным образом,
![]() .
.
Следовательно,
![]() .
.
Далее, при
![]() →
→![]() точки
точки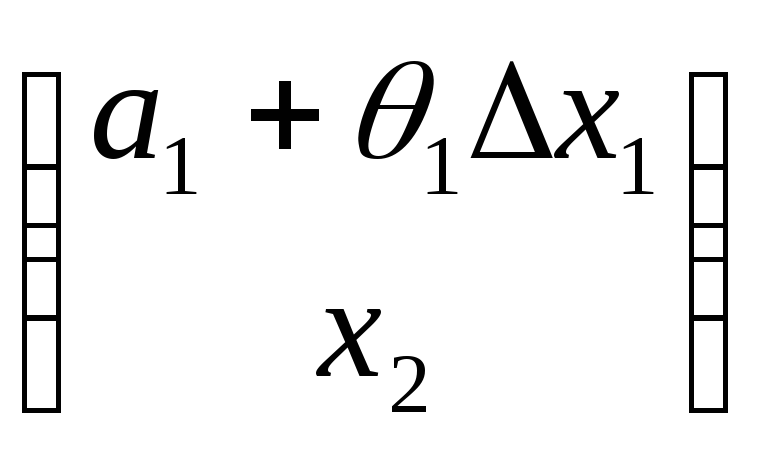 и
и стремятся к точке
стремятся к точке![]() .
.
Непрерывность частных производных в этой точке означает, что их можно представить в виде
![]() ,
,
![]() ,
где
,
где
![]() при
при![]() →
→![]() .
.
Поэтому получаем представление для приращения функции:
![]() ,
,
означающее
дифференцируемость функции
![]() .Случай
.Случай![]() рассмотрен.
рассмотрен.
В общем случае
пусть
![]() принадлежит рассматриваемой окрестности
принадлежит рассматриваемой окрестности![]() .
При этом все точки
.
При этом все точки![]() так же принадлежат рассматриваемой
окрестности. Приращение функции
так же принадлежат рассматриваемой
окрестности. Приращение функции![]() представим в виде
представим в виде
![]() (4)
(4)
и рассмотрим разности
![]() , (5)
, (5)
составляющие в сумме приращение (4).
Положим
![]() (то
есть фиксируем все переменные, кроме
(то
есть фиксируем все переменные, кроме![]() ).
Тогда рассматриваемая разность (5) имеет
вид
).
Тогда рассматриваемая разность (5) имеет
вид![]() .
Функция
.
Функция![]() по условию дифференцируема на отрезке,
соединяющем
по условию дифференцируема на отрезке,
соединяющем![]() и
и![]() .
Значит, она непрерывна на этом отрезке
и можно применить теорему Лагранжа,
согласно которой
.
Значит, она непрерывна на этом отрезке
и можно применить теорему Лагранжа,
согласно которой![]() ,
где
,
где![]() .
Но
.
Но![]() .
По условию непрерывности частных
производных
.
По условию непрерывности частных
производных![]() ,
где
,
где![]() при
при![]() .
.
Поэтому каждая из
разностей (5) имеет вид
![]() ,
а приращение (4) совпадает с (3) из
определения дифференцируемости. ◄
,
а приращение (4) совпадает с (3) из
определения дифференцируемости. ◄
Замечание.
Непрерывность частных производных не
является необходимым условием
дифференцируемости функций. Например
можно доказать, что функция 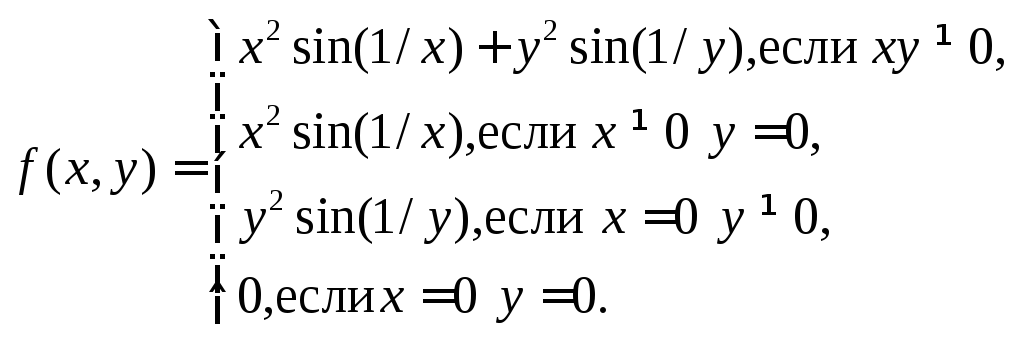 дифференцируема в точке
дифференцируема в точке
![]() ,
но частные производные в этой точке не
непрерывны.
,
но частные производные в этой точке не
непрерывны.
Замечание.
Тем не менее, для функции
![]() частные производные в точке
частные производные в точке![]() равны
0, так как
равны
0, так как![]() и
и![]() (в остальных точках
(в остальных точках![]() ,
,![]() и ясно, что эти производные терпят разрыв
в точке
и ясно, что эти производные терпят разрыв
в точке![]() .
Но функция не дифференцируема в точке
(0,0) , так как её приращение
.
Но функция не дифференцируема в точке
(0,0) , так как её приращение![]() не имеет вида
не имеет вида
![]() ,
где
,
где
![]() при
при![]() .
Действительно, полагая
.
Действительно, полагая![]() и предполагая, что
и предполагая, что![]() ,
,
получаем
![]() ,
или
,
или![]() что невозможно, так как при
что невозможно, так как при![]() правая часть стремится к 0, а левая нет!
правая часть стремится к 0, а левая нет!
