241
Лекция 30
3.13. Электромагнитные колебания
В электрической цепи, содержащей конденсатор и катушку индуктивности (или проводники, обладающие отличными от нуля ёмкостью и индуктивностью) – колебательном контуре – могут возникать электромагнитные колебания. Если сообщить конденсатору заряд и замкнуть цепь, то конденсатор будет разряжаться через катушку. По катушке будет идти переменный ток, который по закону электромагнитной индукции будет создавать в катушке индуцированное электрическое поле, препятствующее изменению тока. Конденсатор будет разряжаться и перезаряжаться, а ток в цепи расти, убывать и менять направление: заряд конденсатора и ток в цепи будут изменяться периодически, т. е. будут происхо-
дить электромагнитные колебания.
3.13.1. Свободные незатухающие колебания (R = 0)
Схема электрической цепи, в которой происходят свободные незатухающие электромагнитные колебания, представлена на РИС. 30.1. Так как сопротивление цепи равно нулю, ток будет изменяться по модулю и направлению, а конденсатор перезаряжаться неограниченно долго – возникнут свободные незатухающие электромагнитные колебания.
Обобщённый закон Ома для контура 12 (1 и 2 – обкладки конденсатора)
Es – ЭДС самоиндукции – единственная ЭДС в этой цепи. Разность потенциалов между обкладками конденсатора
|
по закону электромагнитной индукции |
|
|
|
|
Es L |
dI |
. |
(30.3) |
|
dt |
|
|
|
|
|
По определению силы тока |
I |
dq |
. Подставив это выражение, а также (30.2) и |
|
dt |
|
|
|
|
|
|
|
|
|
|
|
(30.3) в уравнение (30.1): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
2 |
|
|
|
|
|
|
|
L |
d q |
0 |
, |
|
|
|
C |
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2q q 0 . dt2 LC
Это дифференциальное уравнение свободных гармонических колебаний (см. 1.14.2).
, запишем его в стандартном виде (16.1)
d2q ω2q 0 . dt2 0
Общее решение этого уравнения
A и φ – постоянные интегрирования, которые находятся из начальных условий.
Собственная циклическая частота колебательного контура
период свободных незатухающих электромагнитных колебаний
|
Зависимость тока от времени |
|
|
|
I t |
dq |
Aω0 sin ω0t φ . |
|
dt |
|
|
|
Пусть в начальный момент времени заряд конденсатора равен q0, а тока в цепи нет. Подставим начальные условия в общее решение (30.4) и формулу (30.5):
q t q cosω t, |
|
0 |
0 |
|
|
|
I t qω sinω t. |
|
0 |
0 |
Напряжение на конденсаторе
Графики зависимостей q(t) и I(t) при указанных начальных условиях показаны на РИС. 30.2А, Б. Видно, что ток опережает заряд конденсатора (и напряжение на кон-
Энергия электромагнитного поля в колебательном контуре (энергия колебательного контура) складывается из энергии электрического поля конденсатора и энергии магнитного поля катушки:
|
2 |
|
LI |
2 |
|
2 |
|
LI |
2 |
W |
q |
|
|
|
q |
|
|
|
|
|
m |
|
m |
|
|
|
|
|
|
|
|
|
2C |
|
2 |
|
2C |
|
2 |
где qm, Im – соответственно амплитуды заряда конденсатора и тока в цепи. Студенты доказывают утверждение (30.6) самостоятельно.
243
q q0
–q
а
I
q0ω0
–q0ω0
б
Рис. 30.2
3.13.2. Свободные затухающие колебания
Пусть теперь электрическое сопротивление цепи отлично от нуля (см. схему на РИС. 30.3, содержащую элемент R).
|
|
|
|
|
L |
|
|
|
|
|
Обобщённый закон Ома для участка цепи 12: |
|
|
|
|
|
|
|
|
|
|
|
|
φ1 φ2 |
Es IR . |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
(30.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим в это уравнение выражения (30.2) и (30.3): |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
L |
dI |
IR . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 30.3 |
|
|
Учитывая, что I |
dq , запишем это уравнение как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
R dq |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d q |
|
|
|
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
2 |
L dt |
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначим |
1 |
|
ω2 |
, |
R |
2β , где β – коэффициент затухания; получим уравнение |
|
LC |
L |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(16.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
244
2 |
|
|
dq |
|
|
d q |
2β |
2 |
|
|
2 |
|
ω q 0 |
(30.8) |
dt |
|
dt |
0 |
|
|
|
|
– дифференциальное уравнение свободных затухающих колебаний (см. 1.14.3). Это однородное дифференциальное уравнение второго порядка с постоянными ко-
эффициентами. Его характеристическое уравнение
Корни этого уравнения
λ1,2 β 
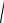 β2
β2
Эти корни могут быть как действительными, так и комплексными. Общее решение дифференциального уравнения (30.8)
|
|
|
|
|
|
q t A1e |
λ t |
A2e |
λ t |
, |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 и A2 – постоянные интегрирования. |
|
|
|
|
|
1. Сильное затухание (β ≥ ω0) |
|
|
|
|
|
|
|
|
|
|
Корни характеристического уравнения (30.9) |
– |
q |
действительные. Общее решение дифференци- |
|
ального уравнения (30.8) |
|
|
|
|
|
|
|
|
|
|
q0 |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
2 |
2 |
t |
|
|
β |
2 |
2 |
t |
|
|
|
|
q t A e |
|
β β |
ω |
A e |
|
β |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
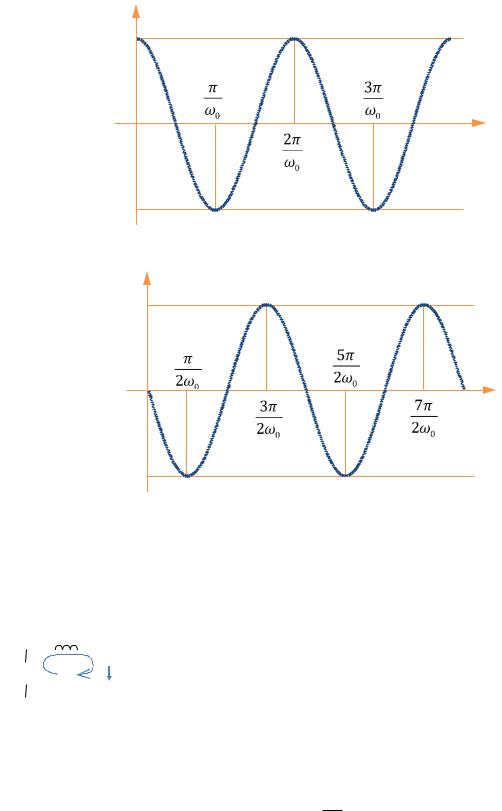
– апериодическое решение (разрядка конденсато-
ра). График этого решения представлен на
РИС. 30.4 (q0 – заряд конденсатора при t = 0). 0 t
2. Слабое затухание (β < ω0) |
Рис. 30.4 |
|
Корни характеристического уравнения (30.9) – комплексные. дифференциального уравнения (30.8)
|
|
β i |
2 |
β |
2 |
|
t |
|
|
β i |
2 |
β |
2 |
t |
|
|
|
|
|
2 |
2 |
|
|
|
|
ω |
|
|
ω |
|
|
βt |
|
i |
t |
|
i |
q t A e |
|
0 |
|
|
|
A e |
|
0 |
|
|
|
e |
A e |
ω |
β |
A e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
Обозначим
ω
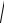 ω02 β2
ω02 β2
–циклическая частота свободных затухающих колебаний. Общее решение удобно представить в виде
q t A e βt cos ωt φ |
, |
(30.10) |
0 |
где A0 и φ – постоянные интегрирования, значения которых определяются из начальных условий.
Период затухающих колебаний
Амплитуда затухающих колебаний
A t A0e βt ;
245
затухающие колебания можно рассматривать как гармонические колебания с переменной амплитудой:
q
График функции (30.10) при φ = 0 q
t Acos ωt φ .
показан на РИС. 30.5.
Рис. 30.5
Зависимость тока в цепи от времени
|
|
I t |
dq |
A e |
βt |
βcos ωt φ ωsin ωt φ |
A e |
βt |
β |
2 |
2 |
|
|
|
|
|
|
|
ω |
|
|
|
|
|
dt |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
cos ωt |
φ |
|
ω |
|
sin ωt |
|
|
|
|
βt |
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
A e |
β |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ω sin ωt φ θ ; |
|
β |
2 |
ω |
|
|
|
|
|
β |
2 |
ω |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin θ |
|
|
|
|
|
cos θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgθ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ток отстаёт от напряжения по фазе на π θ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Введём ещё некоторые характеристики затухающих колебаний. |
|
|
|
Логарифмический декремент затухания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ ln |
A t |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A t T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим логарифмический декремент через другие характеристики колебаний:
δ ln |
A e |
βt |
βT |
2πβ |
|
|
|
|
. |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
A e |
βt |
e |
βT |
|
ω |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Время релаксации – время, за которое амплитуда затухающих колебаний уменьшается в e раз:
246
|
t |
|
|
A e |
βt |
|
|
|
|
A |
|
e |
|
|
e |
|
e βτ 1 |
|
A t τ |
0 |
|
|
|
βτ |
, |
A e |
βt |
e |
βτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
1 |
. |
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число колебаний за время релаксации, т. е. число колебаний, за которое их ам-
плитуда уменьшается в e раз,
Отсюда ясен физический смысл логарифмического декремента затухания. Добротность колебательного контура
Эта величина пропорциональна уменьшается в e раз.
Энергия затухающих колебаний
.
за которое их амплитуда
В колебательной системе с затуханием происходит диссипация энергии. Так как электрическое сопротивление цепи отлично от нуля, энергия электромагнитного поля переходит во внутреннюю энергию проводников.
Энергия колебаний пропорциональна квадратам амплитуд всех колеблющихся
Относительное уменьшение энергии за период
При малом затухании (δ << 1) 
2πW
 W
W 
Чем выше добротность колебательной системы, тем медленнее убывает энергия колебаний.
3.13.3. Вынужденные колебания
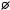 ~
~ 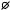
E
Рис. 30.6
Теперь включим в колебательный контур источник с переменной ЭДС (РИС. 30.6), изменяющейся по гармоническому закону:
E U cosΩt |
|
0 |
|
– вынуждающей ЭДС. |
|
Обобщённый закон ома для участка 12: |
|
φ1 φ2 E Es IR . |
(30.11) |
Подставив сюда (30.2) и (30.3), получим |
|
с учётом I
Обозначим,
мет вид
|
|
q |
U0 cosΩt L |
dI |
IR ; |
|
C |
dt |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
dq |
|
|
q |
|
|
|
|
|
|
|
|
|
|
L |
d q |
R |
|
U |
|
cosΩt |
, |
|
|
|
dt |
2 |
dt |
|
C |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2q |
R dq |
|
|
q |
|
|
U0 |
cosΩt . |
|
|
dt2 |
|
LC |
|
|
|
|
L dt |
|
|
|
|
L |
|
|
|
|
|
1 |
|
|
|
|
2 |
, |
R |
2β , а также |
U0 |
|
LC |
ω0 |
L |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d q |
|
2β |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
ω q F cosΩt |
|
|
|
dt |
|
|
|
dt |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Уравнение (30.11) при-
(30.12)
– дифференциальное уравнение вынужденных гармонических колебаний. Это неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Далее рассматриваем случай СЛАБОГО ЗАТУХАНИЯ. |
|
|
|
|
Общее решение дифференциального уравнения (30.12): |
|
|
|
q t A e βt cos ωt φ q cos Ωt φ |
. |
(30.13) |
0 |
0 |
0 |
|
|
общее решение ОДУ частное решение НДУ
Общее решение однородного дифференциального уравнения [(30.8) или (30.12) без правой части] быстро затухает, далее мы его учитывать не будем. Найдём коэффициенты q0 и φ0 в частном решении неоднородного уравнения [и убедимся в том, что это решение действительно имеет вид второго слагаемого в выражении
(30.13)].
Подставим в (30.12):
|
q t q0 cos Ωt φ0 |
, |
|
I t |
dq |
Ωq0 sin Ωt φ0 , |
|
dt |
|
|
|
|
|
d2q |
Ω2q cos Ωt φ ; |
|
dt2 |
|
0 |
0 |
получим
Ω2q0 cos Ωt φ0 2βΩq0 sin Ωt φ0 ω02q0 cos Ωt φ0 F0 cosΩt .
Преобразуем левую часть этого равенства:
|
q |
ω |
Ω |
|
cos Ωt φ |
2βΩsin Ωt φ q |
|
ω |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2βΩ |
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
cos Ωt φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
2 |
Ω |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
Ω |
2 |
|
|
|
2 |
Ω |
2 |
|
|
|
ω |
|
|
|
|
4β |
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
4β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
2 |
Ω |
|
|
|
Ω |
cos Ωt |
φ θ |
|
, |
|
cos θ |
|
|
|
|
|
|
|
|
|
ω |
|
|
|
4β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgθ |
2βΩ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
Ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
|
2 |
4β |
Ω |
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin Ωt φ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin θ
0 |
|
0 |
|
2 |
|
|
|
0 |
|
|
0 |
2 |
|
2 |
|
|
q |
|
2 |
|
2 |
|
θ |
|
F cosΩt |
|
ω |
Ω |
|
4β |
Ω |
cos Ωt φ |
|
Это равенство должно выполняться при любых t, поэтому
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
2 |
2 |
2 |
2 |
Ω |
2 |
F |
, |
q |
|
ω |
Ω |
|
4β |
|
|
|
|
|
φ θ cosΩt. |
|
|
|
|
|
|
cos Ωt |
|
|
|
|
|
0 |
|
|
|
|
|
|
Отсюда получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ θ |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
– колебания заряда опережают вынуждающую ЭДС по фазе на θ;
q |
|
|
|
|
F |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
Ω |
2 |
2 |
2 |
Ω |
2 |
|
|
|
ω |
|
|
4β |
|
– амплитуда заряда конденсатора.
Запишем окончательные выражения зависимостей заряда конденсатора и силы тока в цепи от времени:
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Ω |
2 |
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
|
ω |
|
|
|
|
4β Ω |
|
|
|
|
|
|
|
|
|
|
|
F Ω |
|
|
|
|
|
I0 – амплитуда силы тока |
|
I t |
|
|
|
|
|
|
|
|
sin Ωt θ |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
Ω |
2 |
2 |
|
2 |
Ω |
2 |
|
|
|
|
|
|
|
ω |
|
|
|
|
4β |
|
|
|
|
|
Так как |
|
|
|
|
|
π |
θ |
|
|
|
|
Ωt θ |
π |
, ток отстаёт по |
sin Ωt θ sin θ Ωt cos |
|
|
Ωt |
cos |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
фазе от заряда конденсатора на |
|
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим
Z U0 I0
– полное сопротивление (импеданс) цепи. (Эта величина вводится по аналогии с законом Ома для участка цепи U = IR: если сопротивление R проводника – это коэффициент пропорциональности между током и напряжением на этом участке, то
249
импеданс Z – это коэффициент пропорциональности между амплитудным значением тока и амплитудным значением напряжения на клеммах участка цепи, т. е. вынуждающей ЭДС.)
Выразим полное сопротивление цепи, а также сдвиг фаз между зарядом конденсатора и вынуждающей ЭДС через её параметры R, L, C:
|
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
|
|
|
4β |
Ω |
|
|
|
|
|
|
|
|
|
|
ω Ω |
|
|
|
|
|
|
|
U L |
|
|
1 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F Ω |
|
|
|
|
|
|
|
|
|
|
|
U |
Ω |
|
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
L |
|
|
|
|
L |
|
|
2 |
|
|
|
L |
|
|
|
Ω |
2 |
|
|
|
|
|
Ω |
Ω |
|
|
|
Ω |
2 |
|
2 |
|
|
|
|
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
ΩLC |
|
|
|
|
tgθ |
|
|
|
2RΩ |
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
L |
|
|
|
Ω2L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2L |
|
|
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LC |
|
|
|
|
|
|
|
|
|
ΩLC |
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
R |
2 |
|
|
1 |
|
|
|
|
|
|
, |
tgθ |
|
|
|
|
|
ΩC |
|
ΩL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
2 |
4 |
2 Ω |
2 |
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
4L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
R |
2 |
|
|
R |
2 |
|
|
ΩL |
, |
|
|
|
|
ΩC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ΩL |
|
|
|
|
|
|
|
ΩC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
. |
|
|
|
|
|
|
|
|
(30.14) |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ΩL |
|
|
|
|
|
|
|
|
|
|
ΩC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|










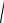 β
β
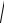

 W
W 
 ~
~