Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4624 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Национальный исследовательский университет «МЭИ»
Предмет:
B-физика
Файл:

Конспект лекций по общей физики (1-4 семестр)

.pdf
Скачиваний:
143
Добавлен:
31.03.2015
Размер:
13.27 Mб
Скачать
☆

 

 

 

 

 

 

120

 

 

 

 

 

 

y

 

t

y′

 

 

 

t′

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m0

 

 

 

 

 

 

 

 

m0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

K′

 

 

 

 

 

 

 

 

 

 

 

K

O′

 

 

 

 

 

 

 

 

 

 

 

x′

 

 

 

 

 

 

 

 

 

 

 

 

 

 

O

 

 

 

 

 

Рис. 15.4

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Определим импульс материальной точки, как в классической механике:

 

 

 

 

 

 

p m0u .

 

 

 

 

 

 

Используя РЕЛЯТИВИСТСКИЙ ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ, получим в системе отсчёта K:

проекция начального импульса системы на ось x

 

 

 

 

 

 

 

 

 

 

P1x 2m0v

,

 

 

 

 

 

проекция конечного импульса

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

P

m

 

 

v u

m

v u

.

 

 

 

 

 

 

 

2x

0

 

 

v

u

0

 

v

u

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c2

 

 

 

c2

Видно, что P1x ≠ P2x. Получается., что в системе отсчёта K закон сохранения не выполняется, чего не может быть.

Подберём такое выражение для импульса, чтобы py py . (В классической механи-

ке py m0 dydt ; так как dy = dy′, а dt = dt′, то при таком определении

py

py

.) Возь-

мём в качестве элементарного интервала времени собственное время dτ = dτ′. Тогда

 

 

 

 

 

 

 

m0

dy

m0

dy

py .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

py

dτ

dτ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Но dτ dt 1

u

, поэтому

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m dy

 

 

m dy

 

 

 

m u

y

 

 

 

 

p

 

 

0

 

 

 

 

 

0

 

 

 

 

 

 

0

 

 

 

 

 

y

dτ

 

 

 

 

u

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

dt

1

c

2

 

 

 

1

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

аналогично

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

px

 

m u

 

, pz

 

m u

 

 

;

 

 

 

 

 

 

 

 

0

x

 

 

0

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

1

u

 

 

 

1

u

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

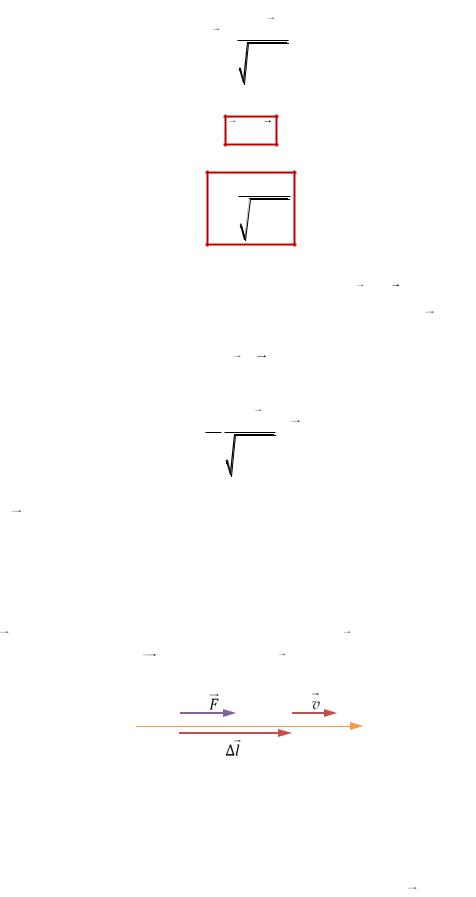
в векторной форме

,

121

p

m u

 

0

 

 

 

 

 

 

 

 

2

 

1

u

 

c

2

 

 

 

 

 

.

Запишем это определение в виде, аналогичном формуле классической механики:

p здесь m – релятивистская масса:

m

mu ,

m

 

 

0

 

 

 

 

2

1

u

c

2

 

 

 

.

1.13.2. Релятивистское уравнение динамики материальной точки

Если материальная точка изолирована, то её импульс

p mu const . Если на точ-

ку действуют другие объекты, то мера взаимодействия – сила F . Запишем уравнение динамики:

 

 

p F

 

t

или, подставляя выражение для релятивистского импульса,

 

 

 

 

 

 

 

d

m u

 

F

 

 

dt

0

u

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

1

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

– релятивистское уравнение динамики материальной точки.

Так как F f v,t и ни время, ни скорость не являются инвариантами преобразо-

ваний Лоренца, то и сила не является релятивистским инвариантом. Поэтому полученное уравнение динамики малополезно для решения задач.

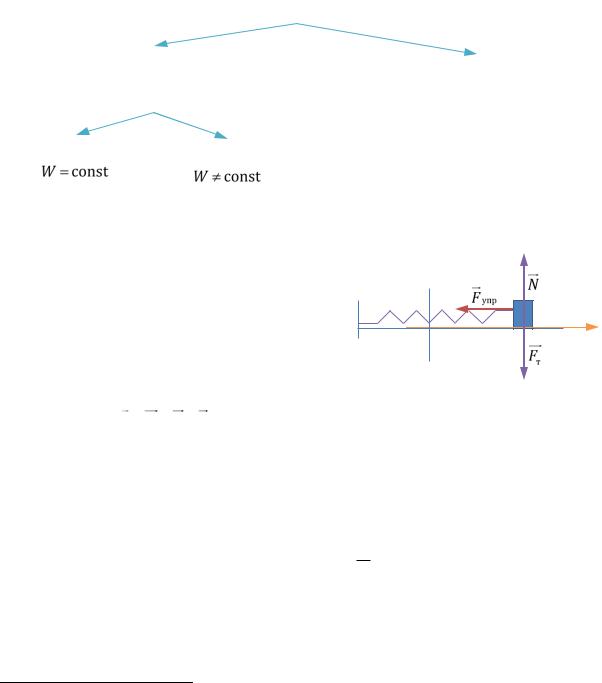
1.13.3. Энергия в релятивистской механике

Пусть тело движется под воздействием других объектов, которое описывается

силой F , направленной параллельно перемещению

l

(РИС. 15.5). Тело разгоняет-

ся от начальной скорости u0 0

до скорости u .

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

O

 

 

 

 

 

 

 

 

 

 

 

t 0

 

 

t 0

 

 

x 0

 

 

x 0

 

 

u 0

 

 

u 0

 

 

Wк 0

Wк 0

 

 

 

 

 

Рис. 15.5

 

 

По теореме об изменении кинетической энергии работа силы F

 

 

 

A

Wк Wк .

 

 

122

Найдём работу и, соответственно, кинетическую энергию тела. Элементарная работа на малом перемещении dl (dl = dx)

δA Fdl

Fdxcos0 Fdx

;

так как из релятивистского уравнения динамики

пульс p mu

δA

d mu

dx ud mu .

dt

 

 

Проинтегрируем это выражение:

F

dp dt

, релятивистский им-

 

 

u

ud mu u mu

u

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

u

 

 

 

 

 

m

 

 

2u du

к

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

A W

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

mudu mu

 

 

2

 

 

 

 

 

 

 

 

 

u

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

 

u

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

c

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m c

2

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

mu

2

 

 

 

c

 

mu

2

m

 

 

 

 

 

 

 

 

 

 

 

 

m c

2

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

u

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

m c

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m u

 

 

 

 

 

 

 

 

 

m u

 

 

m c2 mc2 m c2

,

 

 

 

 

 

0

 

 

 

0

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

u

 

 

 

1

u

 

 

1

u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

2

 

 

 

c

2

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W mc

2

m c

2

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

к

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При u << c

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

 

 

W

m c

2

 

 

 

 

 

 

1 m c

2

1

 

u

 

 

1

 

m u

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

к

 

 

0

 

 

 

u

 

 

 

 

 

 

0

 

 

 

 

 

 

 

2c

2

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

– результат классической механики.

Полная энергия

 

 

2

 

 

 

 

W mc

.

 

 

 

 

 

 

 

Представим

 

 

 

 

2

W m c

2

W mc

 

 

 

к

 

0

 

При u = 0 W = W0 = m0c2;

 

 

 

 

 

W m c2

 

 

 

0

0

 

 

 

.

– энергия покоя.

Энергия покоя может переходить в другие виды энергии.

123

ПРИМЕРЫ

1) Реакция аннигиляции

При взаимодействии частицы и её античастицы они аннигилируют (взаимно уничтожаются) с образованием фотонов. Например, реакция электрона и позитрона

e

 

 

m0

e 2γ

m0

,

m0 = 0

γ – фотон рентгеновского излучения. Массы покоя электрона и позитрона одинаковы (m0), а масса покоя фотона равна нулю. Энергия покоя электрона и позитрона переходит в энергию фотона (энергию электромагнитного поля).

2) Дефект масс

Атомные ядра состоят из нуклонов – протонов и нейтронов (см. РАЗДЕЛ 7.1.1). Массы покоя протона и нейтрона в свободном состоянии соответственно равны mp и mn; масса ядра – mя.

Всегда масса ядра меньше суммы масс составляющих его нуклонов:

m Zm A Z

я

p

здесь Z – число протонов в ядре – заряд ядра, нейтронов в ядре. Разность

m Zm

A Z m

0

p

n

– дефект масс.

mn ,

A – массовое число, (A – Z) – число

mя 0

,

Рассмотрим реакцию синтеза атомного ядра (см. РАЗДЕЛ 7.3.5) – реакцию получе-

ния ядра из отдельных нуклонов. Изменение энергии системы нуклонов

к

 

 

 

0

 

W W

 

m c

 

 

 

 

 

2

 

В замкнутой системе W = 0. Поэтому

 

 

 

 

Wк c

2

m0

 

 

 

 

 

W c

 

 

 

2

 

к

 

 

m

W

 

к

 

 

 

0

 

c

2

 

 

 

m0

.

.

1.13.4. Вектор энергии-импульса

В 4-пространстве оперируют физическими величинами – 4-векторами.

4-вектор энергии-импульса

 

i

W

 

 

c

 

 

 

 

 

 

 

 

 

 

 

 

P

 

px

 

.

 

 

 

 

 

 

p

 

 

 

 

y

 

 

 

 

 

 

 

pz

 

 

 

 

 

 

 

 

 

 

 

 

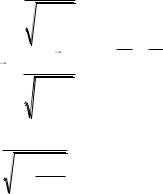
Найдём модуль вектора энергии-импульса:

124

W

 

m c

2

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

u

 

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

p

 

m u

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

1

u

 

 

 

c

2

 

 

 

 

 

 

 

 

 

 

 

 

 

W

m c

2

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

1

c

2

p

2

 

 

 

 

 

 

W

2

 

 

 

 

 

 

 

 

 

 

 

,

 

p

 

u

,

u

 

cp

;

W

c

2

c

W

 

 

 

 

 

 

 

 

 

 

 

W

2

2

2

2

4

inv

 

c p

m c

 

 

 

 

 

0

 

 

– модуль вектора энергии-импульса является релятивистским инвариантом.

125

Лекция 16

1.14. Механические колебания39

1.14.1. Виды колебаний

Колебания – периодические изменения какой-либо физической величины во времени. Система тел, в которой происходят колебания, – колебательная си-

стема.

Колебания могут иметь разную физическою природу, но схожее математическое описание. Сейчас мы будем рассматривать механические колебания.

 

Колебания

 

свободные

вынужденные

колебательная система

при периодическом внешнем

предоставлена самой себе

воздействии

 

 

незатухающие

затухающие

 

 

 

W↓

1.14.2. Свободные незатухающие колебания (собственные колебания)

Рассмотрим свободные колебания пружинного маятника (трения нет) в горизонтальном направлении. Груз – материальная точка массы m – колеблется на пружине жёсткостью k (РИС. 16.1), после того как его вывели из положения равновесия (точка O) и предоставили систему самой себе.

k

m

O

x

 

Запишем II закон Ньютона для груза:

Рис. 16.1

ma Fт N Fупр .

 

Спроецируем это уравнение на ось x. Так как Fупр x = –kx,

 

max kx .

 

По определению, ax d2x2 . Получим дифференциальное уравнение dt

m

d2x

kx 0

 

d2x

dt2

dt2

 

 

 

 

 

Обозначим

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

k

ω02

;

 

 

 

 

m

 

 

 

 

 

 

 

 

k

x

m

 

 

0

.

39 Материал параграфов 1.14 и 1.15 входит в экзаменационную программу II семестра. Материал лекций 16 и 17 может быть, по обстоятельствам, прочитан во II семестре перед темой «ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ» или параллельно материалу этой темы.

126

d

2

x

 

 

 

2

 

 

 

2

ω x 0

(16.1)

dt

0

 

 

 

– дифференциальное уравнение свободных гармонических колебаний.

Это линейное однородное дифференциальное уравнение второго порядка. Его общее решение40

x t Acos ω0t φ

(16.2)

содержит две произвольные константы A и φ. Данные константы определяются из начальных условий.

Пусть при t = 0 x = x0, vx = 0 (груз оттянули на x0 и отпустили без начальной скорости). Первая производная функции (16.2) – проекция скорости груза на ось x

dx v

x

t Aω sin ω t φ .

(16.3)

dt

0

0

 

 

 

 

 

Подставим начальные условия в функции (16.2) и (16.3) и найдём константы A и

φ:

x 0 Acosφ,

 

 

x

0

Acosφ,

 

0 Aω sinφ

 

 

 

 

 

0

Aω sin

v

 

 

x

0

 

 

 

 

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

Частное решение дифференциального уравнения условиях

 

 

φ 0,

 

φ

 

 

A x

.

 

 

 

0

 

(16.1) при данных начальных

x t x0 cosω0t ;

проекции скорости и ускорения на ось x

vx t x0ω0 cosω0t , ax t x0ω02 cosω0t .

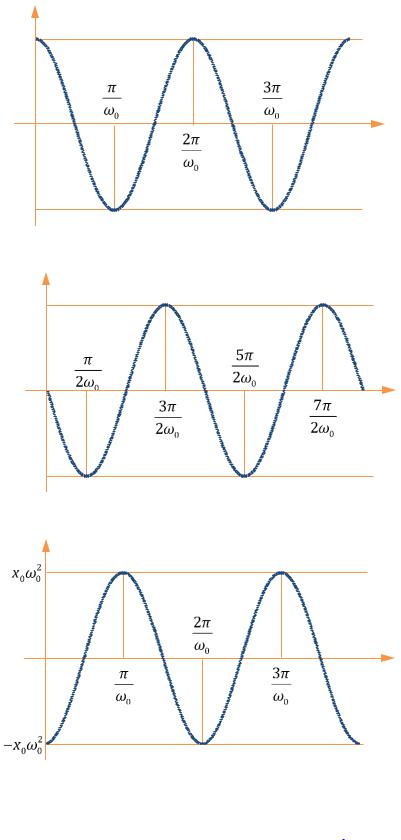
Графики функций x(t), vx(t), ax(t) представлены на РИС. 16.2. Решение (16.2) – гар-

моническая функция.

В общем решении (16.2):

A – амплитуда колебаний – максимальное отклонение колеблющейся величины от равновесного значения;

ω0 – циклическая частота;

выражение в скобках (аргумент косинуса) – фаза колебаний;

φ – начальная фаза.

Введём другие характеристики гармонических колебаний:

период T – время, за которое колебательная система совершает одно полное колебание;

частота ν – число полных колебаний в единичный промежуток времени;

T

ω0

2π

,

ν

ω0

 

1

;

ω0

2π

T

 

 

 

 

 

 

 

 

 

 

 

радс с 1 , ν Гц .

40 Студентам предлагается проверить самостоятельно, является ли формула (16.2) общим решением дифференциального уравнения (16.1).

127

x x0

0

t

–x0

а

vx

x0ω0

0

t

–x0ω0

б

ax

0

t

в

Рис. 16.2

Энергия колебаний (механическая энергия колебательной системы)

W Wк Wп mv2

kx2

const

2π

2

2

 

 

ω0

(студенты проверяют выполнение этого равенства самостоятельно).

128

Демонстрация: Пружинные маятники

ПРИМЕРЫ

1. Математический маятник

 

 

Математический маятник – материальная точка,

 

 

подвешенная на невесомой нерастяжимой нити в одно-

 

 

родном гравитационном поле.

z

 

Найдём период колебаний математического маятника

 

 

 

l

массы m на нити длиной l (РИС. 16.3). Запишем II закон

φ

Ньютона:

 

 

ma Fт T .

 

 

mСпроецируем это уравнение на оси естественной системы координат:

 

man T Fт cosφ ,

 

Рис. 16.3

maτ Fт sinφ .

(16.4)

Груз вращается вокруг оси z по окружности радиуса l. Выразим тангенциальное ускорение маятника через угловое ускорение:

aτ εzl ,

а по определению

εz d2φ . dt2

Подставим (16.5) и (16.6), а также Fт = mg в уравнение (16.4):

 

2

 

 

 

 

 

m

d φ

l

mgsinφ ,

dt

2

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

g

 

d φ

 

sinφ 0.

dt

2

 

l

 

 

 

 

 

 

 

 

 

При малых углах sin φ ≈ φ и это дифференциальное уравнение примет вид

(16.5)

(16.6)

2

 

d φ

dt

2

 

ω2φ 0

0

,

– дифференциальное уравнение свободных гармонических колебаний, где

ω0 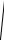gl .

Период колебаний математического маятника T 2π ,

ω0

T 2π gl

зависит только от его длины.

129

2. Физический маятник

Физический маятник – твёрдое тело, которое может вращаться вокруг неподвижной оси, проходящей через

точки этого тела, не являющиеся его центром масс, в од-

z

 

 

нородном гравитационном поле.

 

 

Пусть масса маятника равна m, его момент инерции отно-

 

d

 

 

 

сительно оси маятника равен I, расстояние между цен-

φ

 

C

 

тром масс маятника и его осью z равно d (РИС. 16.4).

 

 

 

 

 

 

Найдём период колебаний маятника.

Запишем основное уравнение динамики вращательного движения:

Рис. 16.4

Iε MF

M

т

 

( N – сила реакции оси маятника). нение на ось маятника:

N

Спроецируем это урав-

 

2

 

I

d φ

dt

2

 

 

 

mgdsinφ

.

При малых углах φ sin φ ≈ φ и

2

 

d φ

dt

2

 

Обозначив

mgd

φ

I

 

0

.

ω

mgd

 

0

I

 

,

получим дифференциальное уравнение свободных гармонических колебаний. Пе-

риод колебаний

T

2π

ω0

,

 

 

 

 

 

T 2π

I

.

 

 

mgd

 

 

 

 

 

 

Приведённая длина физического маятника – длина математического маятника с периодом собственных колебаний, равным периоду собственных колебаний данного физического маятника.

Демонстрация: Математический и физический маятники

Из приведённых выше примеров видно, что свободные незатухающие механические колебания будут гармоническими лишь при малых изменениях колеблющейся величины.

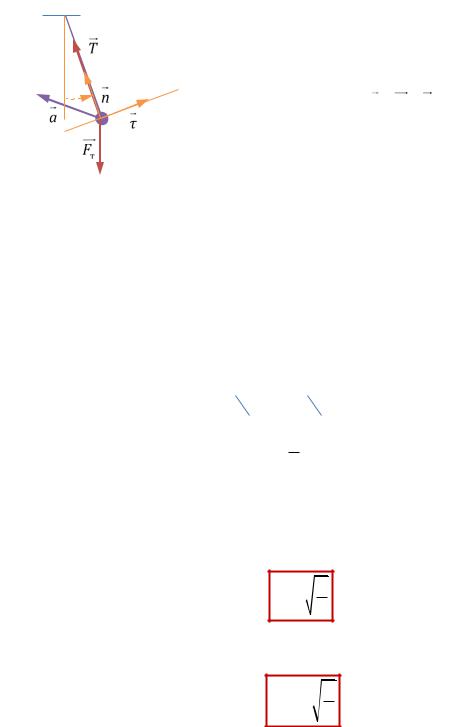
1.14.3. Свободные затухающие колебания

Рассмотрим пружинный маятник (см. 1.14.2), введя силу сопротивления в виде Fсопр rv – сила вязкого трения, r – положительная константа. Колебательная система изображена на РИС. 16.5.

Запишем II закон Ньютона для груза:

ma Fт N Fупр Fсопр .

В проекции на ось x

Соседние файлы в предмете B-физика
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности