
- •7.2. Примеры расчета перемещений в балках методом начальных параметров Пример
- •Решение
- •7.3. Определение перемещений методом Мора
- •7.4. Определение перемещений способом Верещагина
- •7.5. Примеры определения перемещений методом Мора и способом Верещагина Пример
- •Решение
- •4. Определить прогиб сечения с способом Верещагина.
- •Решение
- •Вопросы для самопроверки
- •Содержание и порядок выполнения работы
- •Содержание и порядок выполнения работы
- •Глава VIII. Расчет статически неопределимых плоских систем
- •8.1. Понятие о статически неопределимых системах, степени статической неопределимости, основной и эквивалентной системах, методе сил
- •8.2. Канонические уравнения метода сил
- •8.3. Примеры раскрытия статической неопределимости
- •8.3.1. Расчет многопролетной балки Пример
- •Решение
- •8.3.2. Расчет статически неопределимой рамы Пример
- •8.3.3 Использование свойств симметрии в статически неопределимых рамах Пример
- •Решение
- •8.3.4. Расчет статически неопределимого вала Пример
- •8.3.5. Расчет статически неопределимых систем при растяжении-сжатии Пример
- •Вопросы для самопроверки
- •Контрольная работа № 9.
- •Содержание и порядок выполнения работы
- •Содержание и порядок выполнения работы
- •Содержание и порядок выполнения работы
- •Содержание и порядок выполнения работы
- •Глава IX. Косой изгиб
- •9.1. Понятие косого изгиба
ных долей единицы, следовательно, формулу можно переписать в более простом виде:
![]() .
(7.4)
.
(7.4)
Приравнивая выражения (7.2) и (7.4), получим дифференциальное уравнение упругой балки (7.5):
![]() .
(7.5)
.
(7.5)
При направлении оси y вверх уравнение (7.5) приобретает вид
![]() .
( 7.6)
.
( 7.6)
Систематизируя рассмотренное выше выражение (7.6), можно записать дифференциальные зависимости:
![]()
![]() ,
,
![]() ,
,![]() .
(7.7)
.
(7.7)
Применяя аппарат определенного интегрирования, можно получить универсальные уравнения (7.8), (7.9) позволяющие найти параметры изогнутой оси балки при любых условиях закрепления ее концов, не прибегая к интегрированию дифференциального уравнения:
![]()
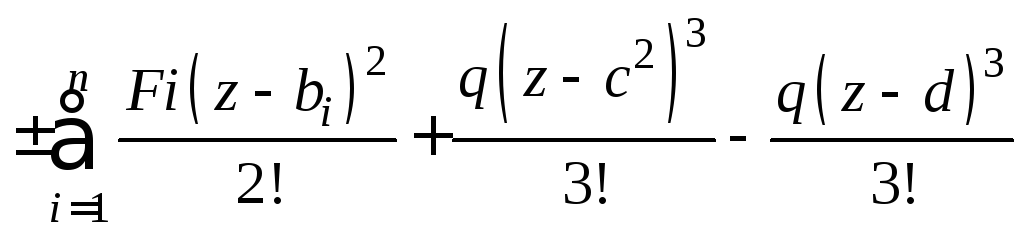 ,
(7.8)
,
(7.8)
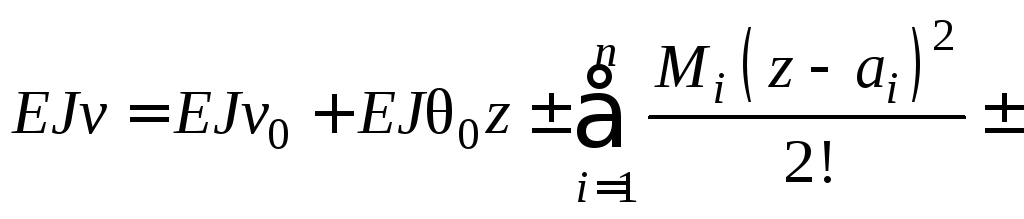
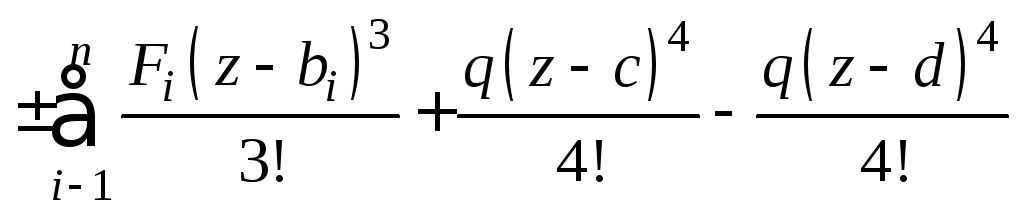
 .
(7.9)
.
(7.9)
З десьai,
bi,
c,
d
– абcциссы
точек приложения сосредоточенных
моментов M,
сил F
и начало равномерно распределенной
нагрузки q
постоянной
интенсивности. В случае действия
распределенной нагрузки, выраженной
по другому закону, необходимо ввести
коррек-тивы в уравнения (7.8), (7.9). M,
F,
q
– внешние
силы и моменты
(включая опорные реакции), расположенные
между данными сечением и началом
координат,
десьai,
bi,
c,
d
– абcциссы
точек приложения сосредоточенных
моментов M,
сил F
и начало равномерно распределенной
нагрузки q
постоянной
интенсивности. В случае действия
распределенной нагрузки, выраженной
по другому закону, необходимо ввести
коррек-тивы в уравнения (7.8), (7.9). M,
F,
q
– внешние
силы и моменты
(включая опорные реакции), расположенные
между данными сечением и началом
координат,
![]() ,
,![]() – прогиб и угол поворота в начале
координат, называемые начальными
параметрами,
а сам метод определения
перемещений с помощью выражений (7.8),
(7.9) называют методом начальных параметров.
Начальные параметры определяют из
условий закрепления балки. Так, для
двухопорной балки (рис. 7.2) а)
– прогиб и угол поворота в начале
координат, называемые начальными
параметрами,
а сам метод определения
перемещений с помощью выражений (7.8),
(7.9) называют методом начальных параметров.
Начальные параметры определяют из
условий закрепления балки. Так, для
двухопорной балки (рис. 7.2) а)![]() = 0 приz
= 0 и
= 0 приz
= 0 и
![]() = 0 приz
= l;
б)
= 0 приz
= l;
б)
![]() = 0 приz
=
a,
= 0 приz
=
a,
![]() = 0 приz
=
a
+ l;
в)
= 0 приz
=
a
+ l;
в)
![]() = 0 приz
= 0,
= 0 приz
= 0,
![]() = 0 приz
= 0.
= 0 приz
= 0.
Для определения перемещений в ступенчатой балке можно использовать общие методы, изложенные в § 7.4, 7.5, или применить видоизмененный метод начальных параметров, что вносит некоторые сложности.
Определение перемещений с помощью универсального уравнения должно включать следующие операции:
Определение реакций на опорах, анализ поперечных сил и изгибающих моментов, подбор сечения балки.
Выбор начала координат, которое принято брать в левой крайней точке рассматриваемой балки.
Проведение произвольного сечения на последнем участке, считая от начала координат, расстояние до которого z. Если распределенная нагрузка обрывается на каком-либо участке (рис. 7.3, а), то ее продлевают до конца балки, а для восстановления действительных грузовых условий на продолжаемой длине прикладывают распределенную нагрузку обратного знака (рис. 7.3, б). Дополнительную и компенсирующую нагрузки принято показывать штриховыми линиями.
З
 апись
уравнений для линейных (v)
и угловых (θ) перемещений применительно
к крайнему правому участку балки.
Сосредоточенная сила и сосредоточенный
момент, приложенные в крайнем сечении
справа, в уравнения не входят.
апись
уравнений для линейных (v)
и угловых (θ) перемещений применительно
к крайнему правому участку балки.
Сосредоточенная сила и сосредоточенный
момент, приложенные в крайнем сечении
справа, в уравнения не входят.Определение из условий закрепления начальных параметров
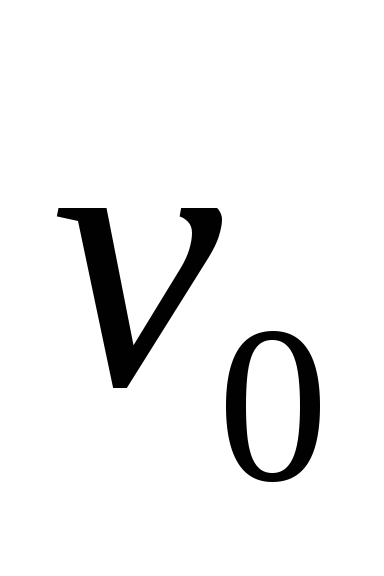 и
и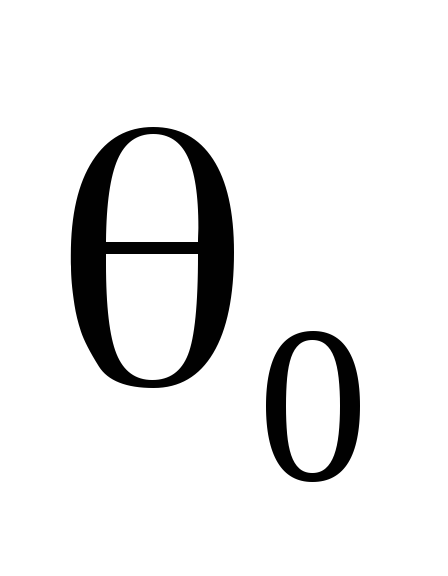 .
Для того чтобы вычислить перемещения
какого-либо
сечения, необходимо в соответствующие
уравнения подставить координату z
(только в те составляющие уравнений
(7.8), (7.9), которые входят в промежуток
между началом координат и рассматриваемым
сечением).
.
Для того чтобы вычислить перемещения
какого-либо
сечения, необходимо в соответствующие
уравнения подставить координату z
(только в те составляющие уравнений
(7.8), (7.9), которые входят в промежуток
между началом координат и рассматриваемым
сечением).
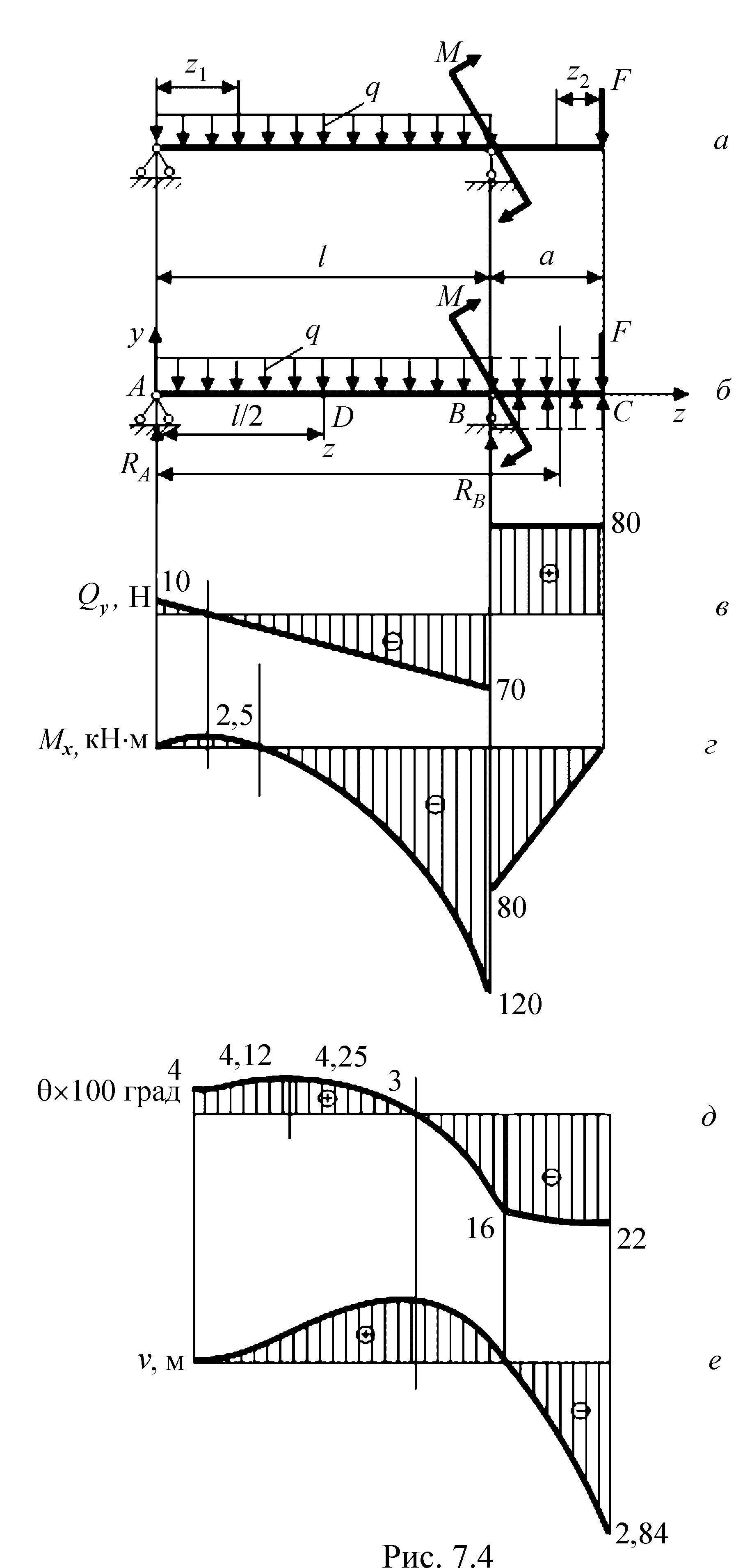
7.2. Примеры расчета перемещений в балках методом начальных параметров Пример
Для
заданной балки (рис. 7.4, а)
подобрать стандартный двутавр из условия
прочности. Определить углы поворота и
прогибы
в различных сечениях, построить
эпюры θ и v;
![]() = 160 МПа,E
=
= 160 МПа,E
=
![]() МПа, M
= 40
МПа, M
= 40
![]() ,
F
= 80 кН, q
= 20 кН/м, l
= 4м,
a
= 1 м.
,
F
= 80 кН, q
= 20 кН/м, l
= 4м,
a
= 1 м.
Решение
1. Определение реакций на опорах, анализ внутренних силовых факторов, подбор сечения.
![]() ,
– M
– F(a
+ l)
–
,
– M
– F(a
+ l)
–
![]() +
+![]()
– 40 –
![]() ,
,
![]()
![]() ,
– M
–
,
– M
–
![]()
= –40 –
![]()
![]()
Проверка:
![]()
Анализ внутренних силовых факторов, подбор сечения:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Эпюры поперечных сил и изгибающих моментов представлены на рис. 7.4, в, г.
Из условия прочности по нормальным напряжениям подбираем сечение:
![]() ,
,
![]()
![]()
По
ГОСТ 8239–89 ближайший номер двутавра №
40
с
![]() =953
см3,
=953
см3,
![]() = 19062 см2.
= 19062 см2.
2. Выбор начала координат в левом краевом сечении, запись универсальных уравнений для последнего участка (рис. 7.4, б).
![]() ,
,
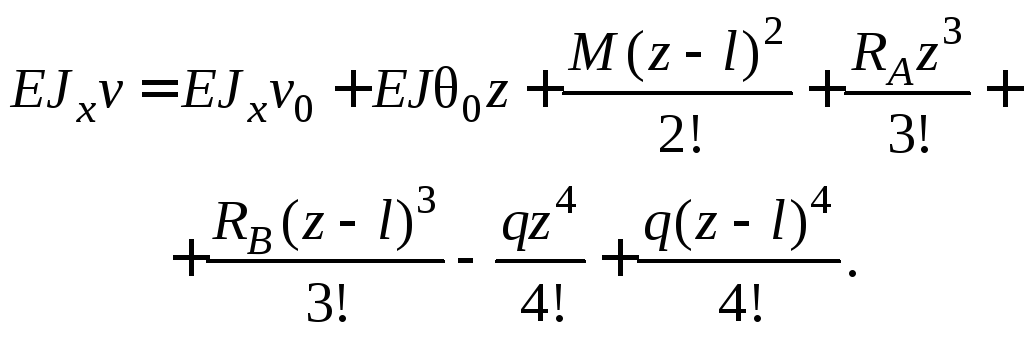
3. Определение
начальных параметров
![]() ,
,![]()
![]() при
при
![]()
![]() ,
т.е.
,
т.е.
![]()
![]() при
при
![]()
![]()
![]()
Окончательные уравнения имеют вид:
![]()
![]()
4. Определение углов поворотов и перемещений в различных сечениях.
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
По расчетным данным построены эпюры углов поворотов θ и перемещений v (рис. 7.4 д, е). Закономерности эпюр θ и v вытекают из дифференциальных зависимостей (7.7):
а) на участках, где
![]() =
0, касательная к кривой θ =f(z)
параллельна оси абсцисс. Там, где на
эпюре моментов скачок, на эпюре θ
наблюдается излом;
=
0, касательная к кривой θ =f(z)
параллельна оси абсцисс. Там, где на
эпюре моментов скачок, на эпюре θ
наблюдается излом;
б) если на протяжении какого-либо участка изгибающий момент равен нулю, то эпюра θ прямоугольна, а эпюра v выражена прямой наклонной линией;
в) на участках, где изгибающий момент постоянный, эпюра θ – прямая наклонная линия, эпюра v – парабола второго порядка;
г) вогнутость на криволинейных участках эпюры θ направлена в сторону эпюры Qy (рис. 7.4 в, д). Вогнутость на криволинейных участках эпюры v направлена в сторону изгибающего момента Mx (рис. 7.4 г, е);
д) в тех сечениях, где θ = 0, на эпюре v наблюдается аналитический максимум или минимум;
е) в сечениях балки, где есть промежуточные шарниры, на эпюре θ будут скачки, на эпюре v – изломы.
7.3. Определение перемещений методом Мора
Практическое применение метода начальных параметров, также как и непосредственное интегрирование дифференциального уравнения упругой линии для некоторых систем имеет сложности. В практике обычно возникает необходимость оценки перемещений в конкретных сечениях конструктивных элементов. Эту задачу успешно решил немецкий ученый Отто Христиан Мор в 1874 г. Метод Мора является универсальным методом определения линейных и угловых перемещений, возникающих в любой стержневой системе от произвольной нагрузки.
В большинстве случаев при определении перемещений в балках, рамах, в арках можно пренебречь влиянием продольных деформаций и деформаций от сдвига, учитывая лишь перемещения, вызываемые только изгибом и кручением. В этом случае для плоской системы интеграл Мора имеет вид
 (7.10)
(7.10)
В случае пространственного нагружения
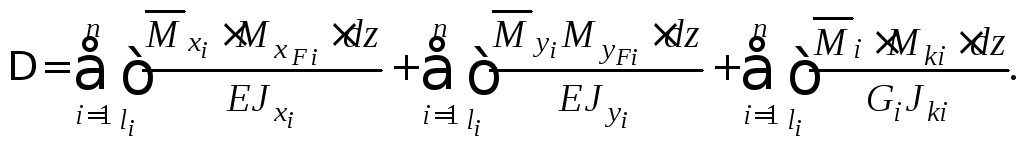 (7.11)
(7.11)
В случае растяжения или сжатия сохраняется лишь член, содержащий продольную силу:
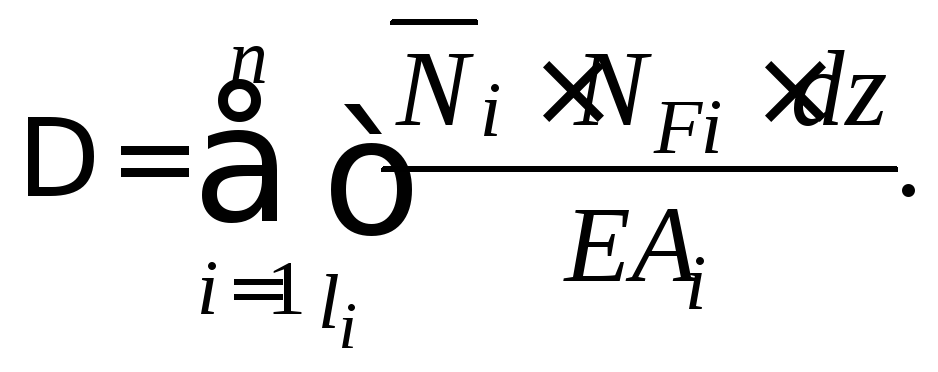 (7.12)
(7.12)
Для системы, испытывающей только кручение,
![]() (7.13)
(7.13)
В формулах
(7.10)–(7.13)
![]() ,
,![]() ,
,![]() – грузовые внутренние силовые факторы
наi-м
участке: соответственно изгибающий
момент, продольная сила и крутящий
момент от внешней нагрузки;
– грузовые внутренние силовые факторы
наi-м
участке: соответственно изгибающий
момент, продольная сила и крутящий
момент от внешней нагрузки;
![]() ,
,![]() ,
,![]() – единичные силовые факторы –
соответственно изгибающий момент,
продольная сила, крутящий момент наi-м
участке от силы, равной единице,
приложенной в том сечении, где необходимо
найти линейное перемещение, или от
момента, равного единице, приложенного
в сечении определения углового
перемещения;
– единичные силовые факторы –
соответственно изгибающий момент,
продольная сила, крутящий момент наi-м
участке от силы, равной единице,
приложенной в том сечении, где необходимо
найти линейное перемещение, или от
момента, равного единице, приложенного
в сечении определения углового
перемещения;
![]() – длинаi-го
участка;
– длинаi-го
участка;
![]() – модуль сдвига,
– модуль сдвига,![]() – модуль продольной упругости,
– модуль продольной упругости,![]() ,
,![]() ,
,![]() – площадь, момент инерции (при круглом
сечении
– площадь, момент инерции (при круглом
сечении![]() =
=![]() где
где![]() – полярный момент инерции),
– полярный момент инерции),![]() – осевой момент инерции сечения наi-м
участке.
– осевой момент инерции сечения наi-м
участке.
Методика определения перемещений методом Мора может быть сведена к следующим пунктам.
1. Определяют
реакции на опорах, разбивают систему
на участки, выбирают направление обхода
участков, записывают выражения для
грузовых силовых факторов на i-х
участках:
![]() ,
,![]() ,
,![]() .
.
2. Строят вспомогательную систему, которую нагружают единичной нагрузкой в точке, где необходимо определить перемещение. При определении линейного перемещения в заданном направлении прикладывают единичную силу, при определении углового перемещения – единичный момент.
3. Определяют
реакции на опорах для вспомогательной
системы и, соблюдая тот же обход участков,
что и в грузовом состоянии, записывают
на i-х
участках
![]() ,
,![]() ,
,![]() .
.
4. Вычисляют интегралы Мора по участкам в пределах всей системы. В соответствии с вышеуказанным при расчете плоских балок, рам и арок исходят из зависимости (7.10), при расчете ферм – из (7.12), при кручении – из (7.13).
5. Если искомое перемещение имеет положительный знак, то это означает, что его направление совпадает с направлением единичной силы; если отрицательный знак – действительное направление искомого перемещения противоположно направлению единичной силы.
