Используя нормировочное условие

,

получаем

Окончательно получим следующие формулы для вероятностей состояний:

(k = 0,1,2, ... ,n), (3.13)

которые называются формулами Эрланга.

Введем обозначение ρ = λ/μ. Преобразуем выражение (3.13) к виду, удобному для вычислений. С этой целью используем ρ и умножим числитель и знаменатель дроби (3.13) на величину .

, (3.14)

где P(k, ρ) и R(n, ρ) – табличные функции пуассоновского распределения.

Найдем характеристики классической системы массового обслуживания с отказами.

С одной стороны, вероятность обслуживания заявки Р_обс, очевидно, равна вероятности того, что заявка, поступившая в систему, застанет свободным хотя бы один канал:

. (3.15)

С другой стороны, вероятность обслуживания заявки равна относительной пропускной способности системы:

, (3.16)

где λ₀ – плотность потока обслуженных заявок (абсолютная пропускная способность СМО), а – среднее число занятых каналов. Отсюда

. (3.17)

Выражение для среднего числа занятых каналов можно получить и непосредственно через вероятностьР_k:

. (3.18)

Сравнивая (3.17) и (3.18), убеждаемся в том, что

. (3.19)

Вероятность того, что канал занят, будет равна отношению среднего числа занятых каналов к общему числу каналовn:

. (3.20)

Введем в рассмотрение случайную величину Т_з.к – время занятости канала, равное длине промежутка времени, начинающегося с момента поступления заявки в канал, до следующего непосредственного момента освобождения канала. Время занятости канала Т_з.к по условию распределено по показательному закону с интенсивностью μ. Следовательно, среднее время занятости канала

_з.к = М[Т_з.к] = 1/μ.

Временем простоя канала Т_п.к называется длина промежутка времени, начинaющегося с момента освобождения канала, до его занятия следующей заявкой. Среднее время простоя канала _п.к определяется из следующего выражения, имеющего место для эргодической системы, находящейся в стационарном режиме:

,

т.е. вероятность занятости канала равна отношению среднего времени занятости канала к сумме среднего времени занятости канала и среднего времени простоя канала. Отсюда

.

Вероятность полной загрузки системы, т.е. вероятность того, что все каналы будут заняты:

Аналогичным образом могут быть определены и другие характеристики системы.

3.4.2. Системы массового обслуживания с отказами и полной взаимопомощью между каналами

Постановка задачи. На вход n-канальной СМО поступает простейший поток заявок с интенсивностью λ. Интенсивность простейшего потока обслуживает каждого канала равна μ. Если заявка застает все каналы свободными, то она принимается на обслуживание и обслуживается всеми n каналами одновременно. Предполагается, что такое обслуживание возможно и при этом приборы обслуживают заявку параллельно, что равносильно увеличению в n раз интенсивности обслуживания (n). После окончания обслуживания все n каналов освобождаются одновременно.

Если вновь прибывшая заявка застает в системе одну заявку, то она принимается на обслуживание. В этом случае часть каналов продолжает обслуживать первую заявку, а остальные каналы приступают к обслуживанию вновь прибывшей заявки. Распределение каналов по заявкам может производиться любым образом. Если прибывшая новая заявка застает в системе две обслуживаемые заявки и n > 2, то каналы распределяются по всем трем заявкам, и т.д.

Если вновь прибывшая заявка застает в системе k заявок (k = 1,2, ... , n–1), то она принимается к обслуживанию и все n каналов перераспределяются произвольным образом между k + 1 заявками, но так, чтобы все каналы участвовали в обслуживании.

Если вновь прибывшая заявка застает в системе n заявок, то она получает отказ и не обслуживается. Попавшая на обслуживание заявка обслуживается до конца (заявки «терпеливые»).

Если обслуживание какой-либо заявки окончено, то освободившаяся группа каналов присоединяется к обслуживанию остальных заявок, находящихся в системе. Таким образом, при наличии в системе хотя бы одной заявки все n каналов все время будут заняты.

Граф состояний такой системы приведен на рис. 3.7.

Рис. 3.7. Граф состояний СМО с отказами и полной

взаимопомощью между каналами

Для пуассоновских потоков и стационарного режима СМО будет описываться следующей системой алгебраических уравнений:

0 = –λ Р₀ + nμР₁,

.………………

0 = –(λ + nμ)Р_k + λР_k–1 + nμР_k+1 (k = 1,2, ... , n–1),

……………....

0 = λР_n–1 – nμ Р_n.

Используя тот же подход, что и в § 3.4.1, получим

u_i = –λP_i–1+ nμ Р_i (i = 1,2, ... , n),

u₁= 0,

…...…

u_k+1 – u_k = 0 (k = 1,2, ... , n–1),

…..…

u_n = 0,

откуда

.

Введя обозначение χ и используя нормировочное условие, получим

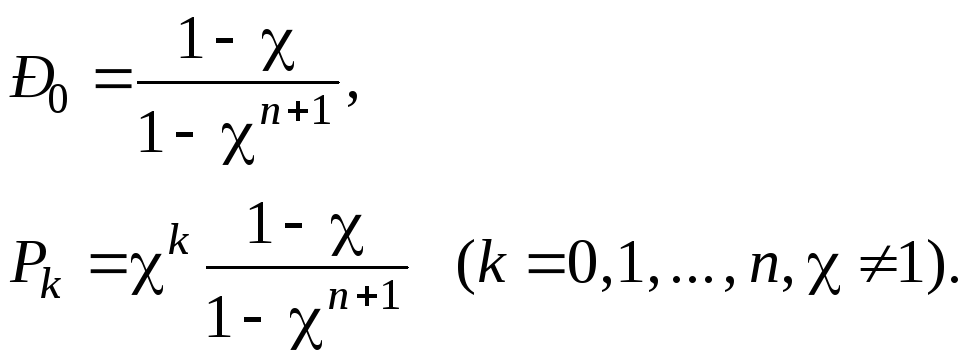
Это выражение справедливо для любых значений χ ≠ 1. При χ = 1 имеет место неопределенность, раскрывая которую, получим

(k = 0,1, ... , n, χ = 1),

т.е. все состояния будут равновероятными.

Определим основные параметры системы.

Вероятность обслуживания заявки определяется из выражения

Найдем среднее число заявок , находящихся в системе:

. (3.21)

Для вычисления суммы, входящей в выражение (3.21), воспользуемся методом дифференцирования рядов [9] и получим

.

При χ = 1 .

Среднее число занятых каналов определяется так:

Для этой системы вероятность того, что любой отдельный канал будет занят, равна вероятности того, что все каналы будут заняты.

.

Среднее время простоя

.

Среднее время занятости канала

.

Аналогичным образом могут быть определены и другие характеристики системы.