По данной матрице построим дифференциальные уравнения вероятностей состояния:

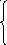
P₀(t + dt) = P₀(t) (1-2_idt)

P₁(t + dt) = P₀(t) 2_idt + P₁(t) (1-_idt)dt

P₂(t + dt) = P₁(t) _idt + P₂(t)

P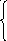^י₀(t) = - 2P₀(t) _i

P^י₁(t) = 2P₀(t) _i – P₁(t) _i

P^י₂(t) = P₁(t) _idt

Начальные условия: P₀(0) = 1; P₁(0) = P₂(0) = 0

Решим систему уравнений с помощью преобразований Лапласа.

Z{ P_i(t)} =P_i(S)

Z{P^י_i(t)} = SP_i(S) - P_i(0)

S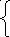P₀(S) - 1 = - 2_i P₀(S)

SP₁(S) = 2_i P₀(S) - _i P₁(S)

SP₂(S) = _i P₁(S)

Решив систему, получим:

P₀(S) =

P₁(S) = =

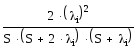
P₂(S) =

Вероятность безотказной работы i-го модуля складывается из вероятностей нахождения его в работоспособном состоянии. Работоспособные состояния i-го модуля: 0 и 1.

R_i(t) = P₀(t) + P₁(t)

Используя обратное преобразование Лапласа, получим:

P₀(t) = e ^{–2 λi t} P₁(t) = 2e^{– λi t} – 2 e ^{–2 λi t}

R_i(t) = 2e ^{– λi t} - e ^{–2 λi t}

Тогда вероятность безотказной работы системы с поэлементным резервированием методом дублирования:

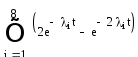R(t) = =

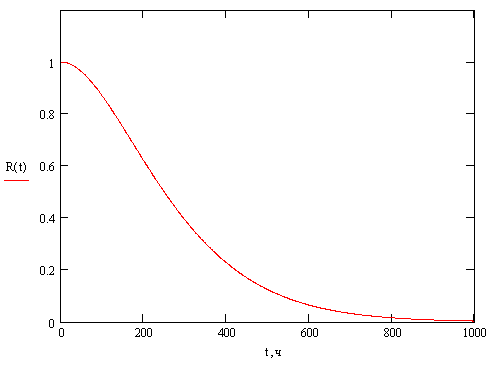
График изменения вероятности безотказной работы неремонтируемой системы с поэлементным резервированием методом дублирования

5. Рассчитать вероятность безотказной работы ремонтируемой системы с общим резервированием методом замещения и построить график ее изменения. (μ = 0.8 ч^-1)

1

8

7

6

5

4

3

2

1^΄

8^΄

7^΄

6^΄

5^΄

4^΄

3^΄

2^΄

Будем предполагать, что в данной ремонтируемой системе:

1. возникновение отказов подчинено экспоненциальному закону распределения;

2. время ремонта – случайная величина с экспоненциальным законом распределения;

3. ремонт оборудования производится сразу же после отказа оборудования;

4. ремонт производится одной ремонтной бригадой (случай ограниченного восстановления);

5. перерывы в работе системы допустимы;

6. отказать может только то оборудование, которое находится в работе;

7. переключающее устройство абсолютно надежно.

Данную систему можно представить следующим образом:

Определим возможные состояния системы:

0 – основное оборудование исправно и находится в работе;

1 – основное оборудование в ремонте, работает резервное оборудование;

2 – и основное, и резервное оборудование неисправны.

Тогда матрица вероятностей переходов системы следующая:

0 1 2

0 1 - _i dt _i dt 0

P = 1  dt 1 –( _i +)dt _i dt

2 0 dt 1- dt

Составим дифференциальные уравнения системы.

P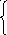₀(t+dt) = P₀(t)(1-_idt) + P₁(t)dt

P₁(t+dt) = P₀(t) _idt + P₁(t)(1 – (+_i))dt + P₂(t)μdt

P₂(t+dt) = P₁(t) _idt – P₂(t)(1 – μdt)

P₀‘(t) = –_i P₀(t)+ P₁(t)

P₁‘(t) = P₀(t) _i – P₁(t) (+_i) + P₂(t)μ

P₂‘(t) = P₁(t) _i – P₂(t)μ

Начальные условия: P₀(t) = 1; P₁(t) = P₂(t) = 0

S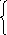P₀(S) – 1 = –_i P₀(S)+ P₁(S)

SP₁(S) = P₀(S) _i – P₁(S) (+_i) + P₂(S)μ

SP₂(S) = P₁(S) _i – P₂(S)μ

Решим систему методом Крамера:

S+_i - 0

Δ = -_i (S+_i +) - = (S+_i)((+S)(S+_i+) - _i ) - _I(+S)

0 -_i (+S)

Δ = (S+0.94)( S+0.016)( S+0.664)

1 - 0

Δ₀ = 0 (S+_i +) - =(+S)(S+_i+) - _i  = S² + S(2 + _i) + ²

0 -_i (+S)

Δ₀ = S² +1,6088S+0,64=(S +0.7204)(S +0.8884)

S+_i 1 0

Δ₁ = -_I 0 -  =_i(+S)

0 0 (+S)

Δ₁ = 0,0088S + 0,00704

P₀(S)====

A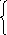+B+C = 1

= 1,6088

= 0.64

A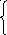= 0.044

B = 1.026

C = -0.072

P₀(S) =

P₀(t) = 0.044* e ^{– 0.94t} + 1.026*e ^{– 0.016t} + 0.072*e ^{– 0.664t}

P₁(S)====

A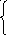+B+C = 0

= 0,0088

= 0.00704

A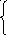= -0.004834

B = 0.012

C = -0.006687

P₁(S) =

P₁(t) = -0.004834* e ^{– 0.94t} + 0.012*e ^{– 0.016t} + -0.006687*e ^{– 0.664t}

Для ремонтируемых систем, для которых возможны перерывы в работе, характеристикой надежности является коэффициент готовности:

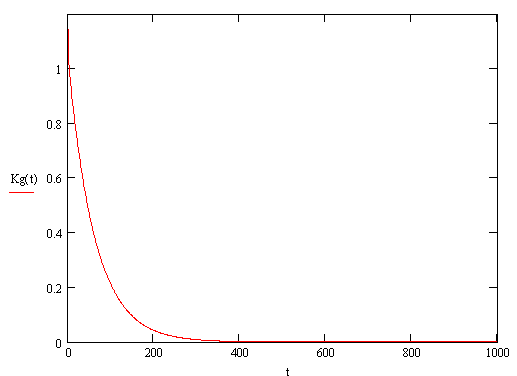
K_Г = P₀(t) + P₁(t) = 0.039166* e ^{– 0.94t} + 1.038*e ^{– 0.016t} + 0.065313*e ^{– 0.664t}

График зависимости безотказной работы ремонтируемой системы с общим резервированием методом замещения: