Лаба 2;

Нижегородский Государственный Технический Университет

им Р.Е.Алексеева

Кафедра: Прикладная математика

Отчет по лабораторной работе №2

Тема «Решение систем линейных уравнений»

Вариант №7

Выполнил: Кокурин М.А.

Студент группы: 11-КСУ-2

Проверил: Белоцерковская И. Е.

Нижний Новгород

2012г.

Оглавление.

Метод Гауса 3

• Ручной счет 3

• Excel 5

• Mathcad 5

• Си ++ 6

Метод простой итерации 5

• Ручной счет 8

• Excel 9

• Mathcad 10

• Си ++ 10

Метод Зейделя 8

• Ручной счет 11

• Excel 12

• Mathcad 13

• Си ++ 13

Список литературы 14

Вывод 15

1 Метод Гаусса.

Запишем систему в виде матрицы, включив коэффициенты уравнений и свободные члены:

A1	15	3	3	0	3
A2	1	14	5	-7	7
A3	-2	1	18	-4	5
A4	3	3	-4	14	4

Алгоритм прямого хода метода Гаусса:

1. Нормируем первое уравнение, разделив каждый член на коэффициент a₁₁.

2. Умножаем коэффициенты полученного уравнения на первые коэффициенты остальных уравнений (a₂₁, a₃₁).

3. Полученные при перемножении результаты последовательно вычитаем из соответствующих уравнений.

В результате матрица принимает следующий вид:

B1=A1/14	1	0,2	0,2	0	0,2
B2=A2-B1*2	0	13,8	4,8	-7	6,8
B3=A3	0	1,4	18,4	-4	5,4
B4=A4-B1*3	0	2,4	-4,6	14	3,4

Видно, что члены, содержащие x₁ исключились из всех уравнений, кроме первого. Далее работаем с системой второго порядка (исключаем члены, содержащие x₂ из третьего уравнения). В результате матрица принимает следующий вид:

C1=B1	1	0,2	0,2	0	0,2
C2=B2/11,8	0	1	0,34	-0,50	0,49
C3=B3-C2*1	0	0	17,91	-3,29	4,71
C4=B4-С2*1,76	0	0	-5,43	15,21	2,21

Видно, что члены, содержащие x₂ исключились из всех уравнений, кроме первого и второго. Далее работаем с системой третьего порядка (исключаем члены, содержащие x₃ из третьего уравнения). В результате матрица принимает следующий вид:

D1=B1	1	0,2	0,2	0	0,2
D2=С2	0	1	0,34	-0,50	0,49
D3=С3/10,735	0	0	1	-0,18	0,26
D4=С4-D3*0,741	0	0	0	14,21	3,64

Наконец, нормируем последнее уравнение:

E1=D1	1	0,2	0,2	0	0,2
E2=D2	0	1	0,34	-0,50	0,49
E3=D3	0	0	1	-0,18	0,26
E4=D4/7,0296	0	0	0	1	0,25

В результате прямого хода метода Гаусса мы получили следующую систему уравнений, имеющую треугольный вид:

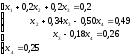
Обратный ход метода Гаусса существенно проще. Сначала из последнего уравнения вычисляем x₄, затем из третьего – x₃, из второго – x₂, наконец, из первого – x₁. В результате получим:

x₄=0,25; x₃ 0,31; x₂ = 0,51; x₁ = 0,03.

1.2 Реализация в Excle

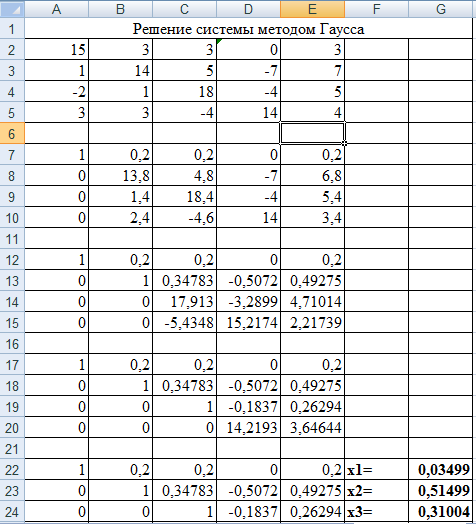
3. Реализация в Mathcad

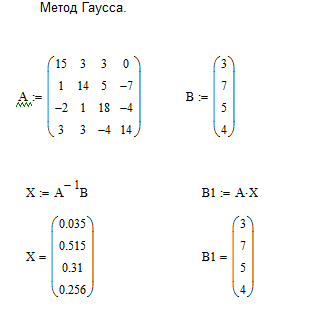
1.4 Реализация в Си++

#include "stdafx.h"

#include<iostream>

#define n 4

#define m 5

using namespace std;

void main()

{

double a[n][m]={{15,3,3,0,3},{1,14,5,-7,7},{-2,1,18,-4,5},{3,3,-4,14,7}};

int i,j,k;

double x[4],c,s;

double d[4][5];

printf("\n matr \n");

for(i=0;i<n;i++)

{for(j=0;j<m;j++)

printf("%5.2f\t",a[i][j]);

printf("\n");}

printf("\n-----------------\n");

for(i=0;i<n;i++)

for(j=0;j<m;j++)d[i][j]=a[i][j];

for(i=0;i<n;i++)

{c=a[i][i];

for(j=0;j<m;j++)

a[i][j]=a[i][j]/c;

if(i!=n-1)

{

for(k=i+1;k<n;k++)

{double r=a[k][i];

for(j=0;j<m;j++)a[k][j]=a[k][j]-a[i][j]*r;

}

}

}

printf("\n 3-naj matr \n");

for(i=0;i<n;i++)

{for(j=0;j<m;j++)

printf("%5.2f\t",a[i][j]);

printf("\n");}

printf("n=%d\tm=%d\t",n,m);

for(i=0;i<n;i++)x[i]=0;

for(i=n-1;i>=0;i--)

{s=0;

for(j=n-1;j>=0;j--)s=s+a[i][j]*x[j];

x[i]=a[i][m-1]-s;

}

printf("\n korni:\n");

for(i=0;i<n;i++)

printf("\n x[%d]=%5.2f",i,x[i]);

printf("\n");

printf("\npoverka po 3-noj matrice:\n");

for(i=0;i<n;i++)

{s=0;for(j=0;j<n;j++)s+=a[i][j]*x[j];

printf("\n %d-e: %5.2f=%5.2f\n",i,s,a[i][m-1]);

printf("\n");

}

printf("\npoverka no isxodnoj matrice:\n");

for(i=0;i<n;i++)

{s=0;for(j=0;j<n;j++)s+=d[i][j]*x[j];

printf("\n %d-e: %5.2f=%5.2f\n",i,s,d[i][m-1]);

printf("\n");

}

char st;

cin>>st;

}

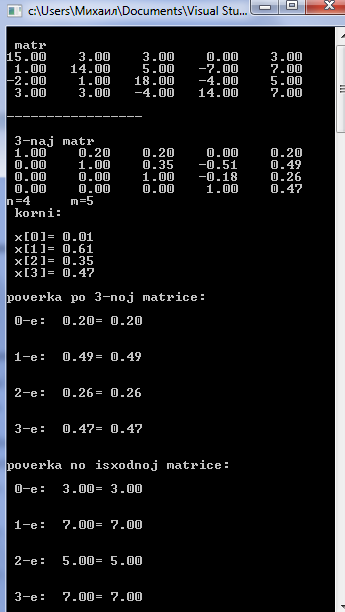
2 Метод простой итерации.

2.1. Ручной счет.

Применим алгоритм метода.

1. Проверка условия сходимости.

15>3+3- да; 14>1+5+-7- да; 18>-2+1+-4- да; 14>3+3+-4- да; сходимость есть.

2. Выбор начального приближения: .

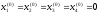3. Запись приведенной системы уравнений:

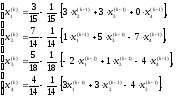
4. Выполним две итерации.

k=1

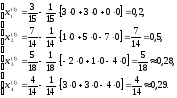
k=2

k=8

Заметим, что точное решение 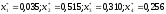в данном методе никогда не будет достигнуто, однако с каждой последующей итерацией вектор неизвестных все ближе приближается к точному решению.

.

2.2 Реализация в Excel

2.3 Реализауия в Mathcad

2.4 Реализация в Си++

3 Метод Зейделя.

3.1 Ручной счет

Применим алгоритм метода.

1. Проверка условия сходимости.

15>3+3- да; 14>1+5+-7- да; 18>-2+1+-4- да; 14>3+3+-4- да; сходимость есть.

2. Выбор начального приближения: .

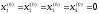3. Запись приведенной системы уравнений:

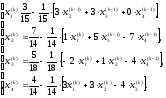
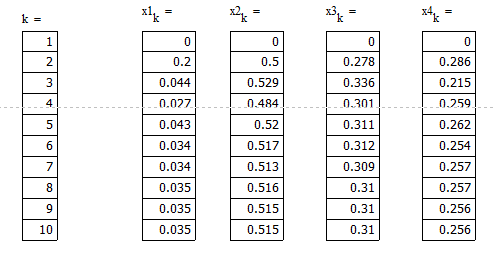
4. Выполним три итерации.

k=1

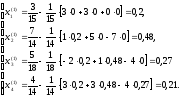
k=2

k=5

Результаты свидетельствуют о более быстрой сходимости метода Зейделя по сравнению с методом простой итерации.

3.2 Реализация в Excel

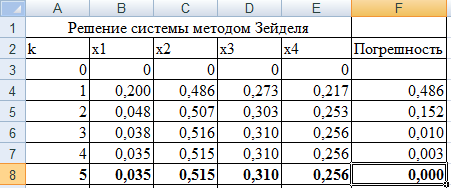
3.3 Реализация в Mathcad.

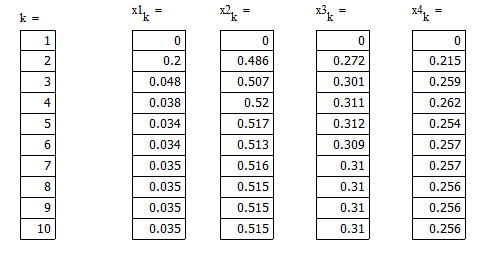
3.4 Реализация в Си++

Список литературы.

1) Соболь, Мешков Б.В. «Практикум по вычислительной математике»

2) Пискунов В.В. «Работа в mathcad»

3) Кирьянов В.Д. «Учебник по Mathcad 14»

4) П. Франка «Учебный курс по C++»

Вывод

В данной лабораторной работе я рассмотрел три метода решения систем линейных уравнений. Метод Зейделя наиболее подходит для моей системы уравнений, так как получилось меньше итераций, чем в других методах и при решении им подставляется только что найденное значение корня, а не предыдущее, за счет чего достигается наиболее уточненное значение корня.