По данной матрице построим дифференциальные уравнения вероятностей состояния:

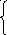
P₀(t + dt) = P₀(t) (1-(₁+…+₈)dt)

P₁(t + dt) = P₀(t) (₁+…+₈)dt + P₁(t)dt

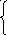
P^י₀(t) = - P₀(t) (₁+…+₈)

P^י₁(t) = P₀(t) (₁+…+₈)

Начальные условия: P₀(0) = 1; P₁(0) = 0

Решим систему уравнений с помощью преобразований Лапласа.

Z{ P_i(t)} =P_i(S)

Z{P^י_i(t)} = SP_i(S) - P_i(0)

S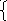P₀(S) - 1 = - (₁+…+₈) P₀(S)

SP₁(S) = (₁+…+₈) P₀(S)

Решив систему, получим:

P₀(S) = 1/(S+(₁+…+₈))

P₁(S) =

Вероятность безотказной работы системы в течение наработки (0; t) определяется суммой вероятностей нахождения системы в работоспособном состоянии. В данном случае работоспособное состояние одно, поэтому надежность системы определяется следующим образом:

R(t) = P₀(t)

Применив обратное преобразование Лапласа, получим:

P₀(t) = L{ P₀(S)} = e ^{- (1+…+8) t} = e ^{– 0,0088 t}

Тогда вероятность безотказной работы неремонтируемой системы:

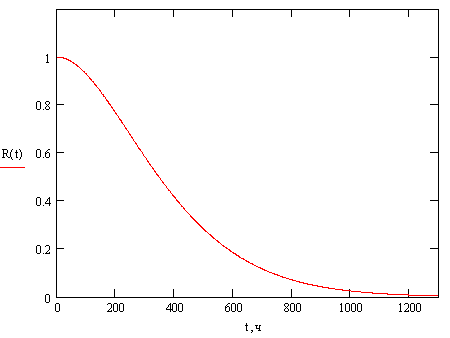
R(t) = e ^{– 0, 0088 t}

График зависимости вероятности безотказной работы неремонтируемой системы от времени:

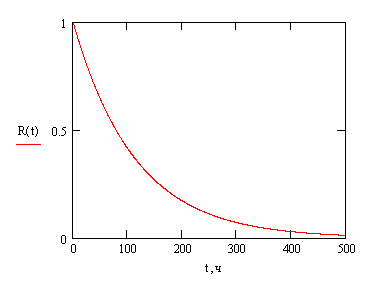
2. Рассчитать вероятность безотказной работы неремонтируемой системы с поэлементным резервированием методом замещения и построить график ее изменения.

Функциональная схема неремонтируемой системы с поэлементным резервированием методом замещения имеет вид:

Рассмотрим резервирование отдельного образца:

Тогда вся система целиком может быть представлена в качестве последовательного соединения таких модулей. Поскольку к отказу системы приведет отказ хотя бы одного из модулей, то вероятность безотказной работы неремонтируемой системы с поэлементным резервированием методом замещения будет определяться следующим образом:

R(t) = П R_i(t)

где R_i(t) – вероятность безотказной работы i-го модуля. При этом считаем, что вероятность отказа каждого модуля не зависит от состояния остальных.

Таким образом, задача сводится к вычислению надежности i-го модуля. Рассмотрим модель надежности такого модуля. При этом будем предполагать, что:

1. возникновение отказов подчинено экспоненциальному закону распределения;

2. модуль откажет, если отказали оба образца;

3. вероятность отказа каждого из двух образцов не зависит от состояния другого;

4. отказать может только тот образец, который находится в работе, а не в резерве;

5. вероятность отказа каждого образца в i-м модуле равна λ_i

Возможные состояния i-го модуля:

0 – i-й образец работает;

1 - i-й образец отказал, работает образец i΄;

2 – образец i΄ отказал.

Матрица вероятностей перехода для i-го модуля:

0 1 2

0 1 - _i dt _i dt 0

P = 1 0 1 - _i dt _i dt

2 0 0 1

По данной матрице построим дифференциальные уравнения вероятностей состояния:

P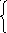₀(t + dt) = P₀(t) (1-_idt)

P₁(t + dt) = P₀(t) _idt + P₁(t) (1-_idt)dt

P₂(t + dt) = P₁(t) _idt + P₂(t)

P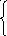^י₀(t) = - P₀(t) _i

P^י₁(t) = P₀(t) _i – P₁(t) _i

P^י₂(t) = P₁(t) _idt

Начальные условия: P₀(0) = 1; P₁(0) = P₂(0) = 0

Решим систему уравнений с помощью преобразований Лапласа.

Z{ P_i(t)} =P_i(S)

Z{P^י_i(t)} = SP_i(S) - P_i(0)

S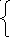P₀(S) - 1 = - _i P₀(S)

SP₁(S) = _i P₀(S) - _i P₁(S)

SP₂(S) = _i P₁(S)

Решив систему, получим:

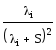
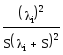
P₀(S) = P₁(S) = P₂(S) =

Вероятность безотказной работы i-го модуля складывается из вероятностей нахождения его в работоспособном состоянии. Работоспособные состояния i-го модуля: 0 и 1.

R_i(t) = P₀(t) + P₁(t)

Используя обратное преобразование Лапласа, получим:

P₀(t) = e ^{– λi t} P₁(t) = λ_i t e^{– λi t}

R_i(t) = e ^{– λi t}(1 + λ_i t)

Тогда вероятность безотказной работы системы с поэлементным резервированием методом замещения:

R(t) = e ^{– λit}(1+ λ_i t) = e ^{– 0,0088 t} (1+ λ_i t)

График изменения вероятности безотказной работы неремонтируемой системы с поэлементным резервированием методом замещения