1. ИСХОДНЫЕ ПОНЯТИЯ

Предмет аэрогазодинамики – изучение законов движения жидкостей и газов и их взаимодействия с твердыми телами. Это изучение мы будем проводить в рамках гипотезы сплошности, смысл которой в следующем.

Известно, что жидкость (или газ) состоит из молекул, которые находятся в хаотическом движении и сталкиваются между собой. Степень разреженности газа можно характеризовать длиной свободного пробега молекул (статистически среднее расстояние между столкновениями любой молекулы с другими молекулами). При нормальных атмосферных условиях в 1 см3 воздуха содержится 2,7·1019 молекул, а длина свободного пробега представляет величину порядка 10-5 cм. На молекулярном уровне изучением движения жидкостей и газов занимается кинетическая теория. Возникающие при этом вопросы носят достаточно специфический характер и являются предметом отдельного изучения.

На основе гипотезы сплошности можно ввести понятие элементарной жидкой частицы (здесь и далее под жидкостью понимается текучая среда, т.е. как собственно жидкость типа воды, так и газ, например, воздух). Это такая частица, размеры которой малы по сравнению с характерными линейными размерами изучаемого течения, однако намного больше длины свободного пробега молекул. Жидкая частица содержит очень много молекул и обладает всеми характерными свойствами жидкости. Ей можно приписать определенные плотность, скорость, давление, температуру и т.п.

Предполагается, что жидкие частицы сплошным образом заполняют все пространство течения, поэтому их параметры можно рассматривать как непрерывные функции координат и времени (хотя, в принципе, в течении допускается наличие поверхностей, на которых параметры терпят разрывы первого рода).

Это позволяет для описания течений жидкостей и газов использовать аппарат математического анализа и смежных разделов математики, изучающих гладкие функции. В частности, при оп-

Стремление объема V к нулю имеет здесь не столько математический, сколько физический смысл – уменьшение объема до элементарной жидкой частицы.

В таком представлении введение понятия жидкой частицы позволяет единообразно рассматривать как движение капельной жидкости, так и газообразной среды и употреблять при этом такие словосочетания, как «несжимаемая жидкость» и «сжимаемая жидкость».

Обычно считается, что среда сплошная, если число Кнудсена Kn = l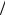L ≤ 0,01 , где l – длина свободного пробега, L – характерный размер рассматриваемого течения; если Kn>0,1 – разреженный газ, если Kn ≈ 0,01÷0,1 – переходный режим течения.

Приведем некоторые основные понятия и определения, используемые при изложении курса.

Укажем сначала основные свойства жидкости, существенно влияющие на уравнения ее движения и методы их решения. Таких свойств три:

•сжимаемость – способность жидкости изменять объем;

•вязкость – способность жидкости сопротивляться деформационному движению;

•теплопроводность – способность жидкости проводить те-

пло.

В зависимости от сочетания этих свойств, учитываемых при постановке задач, рассматриваются различные модели жидкостей:

•несжимаемая, невязкая (идеальная) и нетеплопроводная;

•несжимаемая, вязкая, теплопроводная;

•сжимаемая, невязкая, нетеплопроводная;

•сжимаемая, вязкая, теплопроводная.

При изучении движения газов различают:

•газ совершенный (термодинамически идеальный) – газ, для которого собственный объем молекул пренебрежимо мал и молекулы взаимодействуют только при столкновениях;

•газ реальный. Эта модель принимается для случая, когда не выполняется хотя бы одно из вышеназванных условий.

Если параметры жидкости в каждой точке течения не изменяются во времени, то такое течение называется установившимся

100

или стационарным, в противном случае – неустановившимся или нестационарным.

Если параметры течения зависят от трех пространственных координат, то его называют трехмерным или пространственным, если от двух, то двумерным (например, плоское или незакрученное осесимметричное течение), если от одной координаты, – одномерным. Если, наконец, параметры течения не зависят от пространственных координат, но изменяются с течением времени, то говорят о нульмерном процессе.

1.1. О методе размерностей

Величины, численные значения которых зависят от выбора единиц измерения, называются размерными. Размерность физической величины – характеристика, показывающая связь данной величины с физическими величинами, положенными в основу системы единиц измерения, – записывается в виде произведения символов соответствующих основных величин, возведенных в определенные степени, которые называются показателями размерности. Размерность – это как бы некоторая «окраска» физической величины, позволяющая отличить ее от других физических величин. Эта «окраска» может иметь принципиальное значение. Например, нельзя складывать градусы температуры и метры, ибо результата такого суммирования просто не существует.

Величины, численные значения которых не зависят от выбора единиц измерения, называются безразмерными. Например, масштаб представления, перегрузка, аэродинамический коэффициент и т.д. Как правило, эти величины представляют собой некоторые отношения размерных величин.

Заметим, что понятие размерных и безразмерных величин является иногда относительным. Например, величина угла может выражаться или в радианах (безразмерная), или в градусах (размерная).

Однако различная «окраска» физических величин может носить и менее принципиальный характер. Например, энергия может быть измерена килограммометрами, джоулями, калориями, тоннами угля, килограммами урана, рублями и т.п. Отсюда возникает необходимость вводить ту или иную систему единиц измерения для сравнения величин одной физической природы.

101

Итак, физические величины выражаются числами, которые получаются путем измерения. Измерение – это прямое или косвенное сопоставление некоторой величины с единицей ее измерения.

Величины, для которых единицы измерения вводятся из опытов с помощью эталонов, называются первичными (основными).

Единицы измерения для величин, которые получаются на основании определения этих величин через первичные, называются производными (вторичными).

Выбор основных единиц измерения не однозначен. Он определяется практической целесообразностью и возможностью их воспроизведения. При этом количество основных величин должно быть наименьшим.

Для геометрических задач достаточно одной основной единицы измерения – некоторой эталонной длины. Через эту единицу выражаются единицы измерения площадей и объемов, которые являются производными единицами.

Для задач кинематики необходимо добавить единицу измерения времени.

Для задач динамики к единицам измерения длины и времени добавляется единица измерения массы (или силы).

Добавляя единицу измерения температуры, мы можем решать задачи термодинамики, присоединив единицу измерения электрического тока – задачи электромагнетизма, единицу измерения силы света – задачу фотометрии.

Совокупность основных единиц измерения, достаточных для измерения характеристик рассматриваемого класса явлений, называется системой единиц измерения. Совокупность систем измерения, различающихся только величиной основных единиц измерения, называется классом систем единиц.

Выражение производной единицы измерения через основные называется размерностью. Если, например, обозначить L – символ единицы длины, M – символ единицы массы, T – символ единицы времени, Θ – символ единицы температуры, а размерность некоторой величины a – через [a] (символ Максвелла), то

она может быть записана в виде формулы [a]= M m Ll T t Θϑ , где m, l, t, ϑ – показатели. Отметим, что существует строгое доказательство этой формулы.

102

Безразмерная величина имеет формулу размерности

[a]= M 0 L0T 0 Θ0 .

Для записи формулы размерности некоторой величины используется соотношение, связывающее эту величину с основными единицами измерения. Так, например, для скорости имеем v = L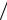T → [v] = LT −1 , для силы – F = mW → [F ] = MLT −2 .

Более подробная иллюстрация сказанного представлена таблицей, где указаны формулы размерностей физических величин, наиболее часто встречающихся в механике.

Особо подчеркнем, что формула размерности имеет вид степенного одночлена. Укажем при этом, что она позволяет легко переходить к другой системе единиц того же класса. Например:

g= 980,665 см с2 = 980,665 0,01м = 9,80665м с2 ,

с2

v=10 мс =101/36000,001 кмчас = 36 км/час,

p =1 атм =1кгс см2 = 1 9,80665 Н = 9,80665 104 Н/м2. (0,01)2 м2

Отсюда вытекает важное следствие: если уменьшить (увеличить) единицы измерения в αM , αL , αT , αθ раз, то численное

значение физической величины, имеющей размерность [a1],

увеличится (уменьшится) в αM m , αL l , αT t , αθϑ раз. Действи-

тельно, [a2 ]= (LαL )l (TαT )t (MαM )m (Θαθ )ϑ = [a1]αLl αTt αMmαθϑ .

И наконец, в теории размерностей ставится задача изучения физических явлений, исходя только из общих соображений размерности. При этом основной получаемый здесь результат (так называемая Пи-теорема) не предполагает использование какихлибо экспериментальных закономерностей или же решения уравнений, описывающих явление и, более того, не используются никакие фундаментальные физические законы и даже рассматриваются такие явления, для описания которых физические законы пока неизвестны. Более общего подхода к изучению физических явлений не существует. Здесь «почти из ничего» могут быть получены весьма важные результаты.

Козьма Прутков был лишь отчасти прав, когда говорил, что «нельзя объять необъятное…». Он должен был добавить при этом: «если не пользоваться методом размерностей». Метод размерностей работает в очень широком диапазоне порядков величин, он позволяет оценивать размеры Вселенной и характеристики атомного ядра, проникать внутрь звезд и находить ошибки у писателей-фантастов, изучать волны на поверхности воды и т.д.

Столь широкие возможности метода размерностей здесь не рассматриваются. Мы ограничимся лишь некоторыми вопросами гидромеханики, но чуть позже.

104

Приведенные рассуждения позволяют сформулировать следующие три исходных положения, которые станут основой всех дальнейших результатов.

1.Физические явления происходят в соответствии с законами природы, и следует четко представлять себе совокупность определяющих это явление физических величин.

2.Физические величины определяются размерным образом через некоторые, выбранные нами основные единицы измерения; выше уже были отмечены основные соображения метода размерностей.

3.Запись физической закономерности не зависит от выбора системы единиц измерения. Например, закон Ньютона о том, что сила равна произведению массы на ускорение, вовсе не нуждается в представлениях о размерности.

Пи-теорема. Из сказанного выше следует чрезвычайно важное практическое правило установления физических соотношений, называемое в теории размерностей Пи-теоремой.

Рассмотрим структуру функциональной зависимости между вообще размерными величинами, выражающими собой физическую закономерность, инвариантную относительно выбора сис-

Найдем структуру функции (1.1) в предположении, что эта функция выражает собой некоторую физическую закономерность, не зависящую от выбора системы единиц измерения.

Размерности остальных величин:

[ak +1 ]= A1p1 A2p2 ...Akpk , [an −1 ]= A1q1 A2q2 ...Akqk , [an ]= A1r1 A2r2 ...Akrk .

Изменим теперь единицы измерения величин a1 ,a2 ,...,ak соответственно в α1 ,α2 ,...,αk раз. Численные значения этих ве-

105

личин и величин ak +1 ,...,an в новой системе единиц будут соот-

ветственно равны:

a1′ =α1a1 a′2 =α2a2

.................

ak′ =αkak

ak′ +1 =α1p1α2p2 ...αkp3 ak +1

……….…..

an′ −1 =α1q1α2q2 ...αkq3an −1

an′ =α1r1α2r2 ...αkr3an .

Вновой системе единиц измерения соотношение (1.1) можно записать в виде

Эта запись справедлива, поскольку (1.1) выражает некоторый физический закон, не зависящий от выбора системы единиц измерения.

Воспользуемся выбором α1,α2 , ... ,αk для сокращения числа независимых переменных функции f . Положим

α1 =1/ a1; α2 =1/ a2 ; ... αk =1/ ak , т.е., используя условие независимости записи физической закономерности от выбора системы единиц измерения, новую систему единиц измерения выберем так, чтобы k аргументов функции f имели фиксированные по-

стоянные значения, равные единице. В этой относительной системе параметры ak +1 ,...,an−1 ,an определяются формулами

сят от выбора первоначальной системы единиц измерения, так как имеют нулевую размерность относительно A1 ,A2 ,...,Ak .

106

Очевидно также, что значения Π1 ,..., Πn−k −1 , Πn−k вообще не

зависят от выбора системы единиц измерения, через которые выражаются k единиц измерения для размерно-независимых величин a1 ,a2 ,...,ak . Следовательно, величины Π1 ,..., Πn−k −1 , Πn−k

можно рассматривать как безразмерные. Поэтому в любой систе-

комбинации из n размерных величин. Этот общий вывод теории размерностей известен под названием Пи-теоремы.

Если некоторая безразмерная величина является функцией ряда размерных величин, то эта функция может зависеть только от безразмерных комбинаций, составленных из всех определяющих ее размерных величин.

Всякое физическое соотношение между размерными величинами можно сформулировать как между безразмерными. В этом, собственно, и заключается источник полезных приложений метода теории размерностей к исследованию физических задач.

Для определения структуры безразмерных комплексов записывается соотношение, связывающее определяющие рассматриваемое явление параметры в виде степенного одночлена:

an =a1n1an2 2 ...annn−1−1 . Показатели степеней ni пока неизвестны и

требуют записи уравнений для их определения. Это соотношение переписывается в виде формулы размерности:

[an ]= [a1 ]n1 [a2 ]n2 ...[an−1 ]nn −1 .

Приравниваются показатели степеней основных единиц измерения. В результате получается система k линейных уравнений. При n −k =1 задача о выборе критериев решается однозначно. В случае n −k >1 решение задачи становится неоднозначным. Тогда полагают, что k показателей степеней являются ос-

107

новными, а остальные n −k выражаются через них с помощью системы линейных уравнений. Выбор основных показателей в определенной степени произволен.

В соотношении, связывающем определяющие параметры явления, после подстановки найденных показателей ni произво-

дится группировка сомножителей таким образом, чтобы образовались комбинации, имеющие один произвольный показатель. Эти комбинации объявляются критериями подобия.

Сделаем теперь два замечания, упрощающие процедуру применения Пи-теоремы.

Замечание 1. Если n −k >1 , то группировку множителей желательно производить таким образом, чтобы получать наиболее распространенные критерии подобия. При этом следует учитывать следующие обстоятельства:

•каждый параметр a i должен входить хотя бы в один без-

размерный комплекс;

•безразмерные комплексы должны быть независимыми, т.е. любой из них не является произведением степеней других.

Замечание 2. Безразмерные критерии подобия делятся на:

•относительные переменные – частные от деления переменных задачи на постоянные параметры: x = x l – безразмерное

расстояние ( l – характерный размер), α – угловая величина, измеряемая в радианах, и т.п.;

•критерии параметрического типа – отношения параметров

одинаковой размерности: l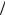d , l 2 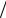S , n = pa 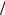pн (степень нерасчетности течения в сопле Лаваля), M =v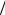a (число Маха) и т.п.;

•критерии комплексного типа, объединяющие параметры

различной размерности: Re = ρμvl (число Рейнольдса) и т.п.

Касаясь задач механики жидкости и газа, можно указать широкий круг вопросов, решение которых связано с применением метода размерностей: изучение турбулентных течений, упрощение решений, например путем сведения системы уравнений в частных производных к системе обыкновенных дифференциальных уравнений, решение некоторых нестационарных задач и многие другие.

В данном пособии мы остановимся лишь на определении аэродинамических характеристик движущихся тел.

108

Об определении аэродинамических коэффициентов лета-

тельных аппаратов. Зададимся вопросом о том, как записать выражение для определения величины аэродинамической силы, воздействующей на тело, движущееся в жидкости со скоростью v . От каких физических параметров зависит величина этой силы? Прежде всего, это размеры и форма тела, его ориентация в потоке. Сюда следует отнести и скорость движения тела, и характеристики среды (плотность, давление, вязкость и другие).

Попробуем указать сначала лишь минимальное число параметров, сочетание которых позволяет определить величину, имеющую размерность силы. Пусть форма тела и его положение в потоке заданы. Нас интересует, от чего в этом случае зависит выражение для величины силы лобового сопротивления X . По условию задачи эта сила должна зависеть явно от величины скорости набегающего потока v . Далее совершенно очевидно, что эта сила зависит и от размеров тела. Пусть l – некоторый характерный размер тела. И наконец, сюда должна быть добавлена величина, включение которой позволяет получить величину X , имеющую размерность силы. Ясно, что следует добавить величину, характеризующую среду. Естественно считать такой величиной плотность ρ набегающего потока. Итак, нас интересует зави-

Запишем соответствующую функциональную связь в виде степенного одночлена: X = ρn1vn2 l n3 . Тогда формула размерно-

сти получает вид MLT −2 = (ML−3 )n1 (LT −1 )n2 Ln3 .

Приравнивая показатели степеней основных единиц измерения, получаем систему линейных уравнений для определения показателей:

M : 1 = n1 ,

L : 1 = −3n1 + n2 + n3 ,

T : −2 = −n2 .

Тогда n1 =1 ; n2 = 2 ; n3 = 2 .

Таким образом, в рассматриваемой постановке задачи выражение силы лобового сопротивления X следует записать в виде

109

Здесь C – постоянный коэффициент. Величина l 2 представляет собой некоторую площадь S . Эта площадь, вообще говоря, может быть произвольной, но выбранной так, чтобы ее легко было задавать. Для бескрылого летательного аппарата в качестве S принимается площадь максимального поперечного сечения (площадь «миделя»), для крылатого – площадь крыла в плане, включая подфюзеляжную часть.

Полезно, кстати, отметить, что в аэродинамике дирижаблей иногда может оказаться более удобным определять характерный геометрический размер исходя из его объема (а не площади).

Рассматривая формулу (1.5), укажем также, что в ней принято использовать комплекс q = (1/2) ρv2 , называемый скоростным напором, определяемым по параметрам набегающего потока. Множитель 1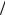2 добавляется исходя из базовых представлений

гидрогазодинамики.

Таким образом, для определения величины аэродинамической силы удобнее записывать ее в виде трех сомножителей:

где Cx – коэффициент лобового сопротивления.

Вернемся к выбору функциональной зависимости простейшего вида, но позволяющего из других предпосылок сформировать величину, имеющую размерность силы. Попробуем принять

Здесь вместо величины ρ использована величина p . Такое представление естественно, поскольку давление p является си-

лой, действующей на единицу площади.

Применяя Пи-теорему к функциональной зависимости (1.7), имеем (читателю предлагается это сделать самостоятельно)

Получился парадоксальный результат, заключающийся в том, что значение силы аэродинамического сопротивления не зависит явным образом от величины скорости набегающего потока v . Формула, конечно, правильная, но весьма неудачная. Ко-

110

эффициент C , входящий в нее, является, безусловно, непостоянным, он существенно зависит от величины v . Значит, вариант, предлагаемый зависимостью (1.7), где в качестве определяющей величины взято давление p набегающего потока, неприемлем.

Возникает вопрос о том, влияет ли вообще величина давление набегающего потока на величину силы X . Попробуем увеличить число параметров, определяющих X , добавив в выражение (1.4) параметр p , и рассмотрим вариант

В качестве произвольного показателя здесь естественно принято n2 (поскольку показатель n2 соответствует добавленной

емкостей при постоянном давлении и постоянном объеме (для воздуха γ =1,4 ). Отношение скорости потока к скорости звука

называется числом Маха M =v / a . Это число является одним из важнейших безразмерных параметров потока в газовой динамике. В терминах числа Маха приведенное выше перед формулой

111

(1.10) выражение для коэффициента аэродинамического сопротивления можно записать в виде Cx = 2(γM2 )−n2 . Отсюда видно, что Cx является в рассматриваемом случае функцией числа Ма-

ха: Cx =Cx (M) .

Если теперь список параметров, определяющих величину X , дополнить коэффициентом динамической вязкости μ набегаю-

то, применяя Пи-теорему, можно получить (рекомендуется выполнить самостоятельно)

X =Cx (M, Re)ρv22 S . (1.12)

Здесь безразмерный комплекс Re = (ρvl )μ представляет со-

бой еще один важнейший безразмерный параметр потока – число Рейнольдса, которое определяет влияние вязких свойств жидкости на характеристики ее течения.

Если по аналогии с предыдущим добавить в правую часть

где g – ускорение силы тяжести, то можно получить (рекомендуется выполнить самостоятельно)

Здесь величина Fr =v 2 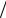gl – число Фруда, характеризующее

влияние сил тяжести.

Приведенные выше безразмерные комплексы M, Re, Fr и не-

которые другие являются критериями динамического подобия, нашедшими широкое применение в механике жидкости и газа.

Выражения для этих критериев можно получить также и из уравнений движения жидкости, рассматривая в них отношения отдельных слагаемых, каждое из которых описывает определенный физический фактор, влияющий на течение жидкости. И такой вывод весьма полезен, правда, в этом случае требуется предварительно иметь запись физических законов в форме соответствующих уравнений.

112

И все же наиболее эффективным и эффектным представляется вывод критериев подобия исходя из наиболее общих соображений, а именно, как это было сделано выше, из соображений размерности, т.е. «почти из ничего».

Проводя аналогичные рассуждения для величины аэродинамического момента (т.е. момента сил, приложенных к телу со стороны потока), например относительно оси z , можно получить

где mz – коэффициент момента аэродинамических сил относи-

тельно оси z .

Продолжая перечисление физических факторов, оказывающих влияние на аэродинамические силы и моменты, которые действуют на летательный аппарат в полете, к названным параметрам (p, μ, g) следует добавить такие геометрические и кине-

матические факторы, как углы атаки α и тангажа γ , угловые скорости вращения аппарата ωx , ωy , ωz , углы поворота органов управления δx , δy, δz и некоторые другие.

Оценку влияния этих факторов принято делать, представляя функциональные зависимости для коэффициентов аэродинамических сил и моментов в виде разложений в ряд Тейлора по указанным выше определяющим факторам. При этом разложения производятся относительно некоторого исходного состояния летательного аппарата, характеризуемого, например, нулевыми значениями углов атаки и тангажа, угловых скоростей вращения и углов отклонения рулей. Обычно в ряде Тейлора удерживаются лишь несколько первых слагаемых. Как правило, это линейные члены, содержащие первые частные производные от аэродинамических коэффициентов по рассматриваемым определяющим параметрам задачи, и иногда нелинейные, содержащие вторые производные, в том числе смешанные. Отметим, что в аэродинамике летательных аппаратов именно так вводятся аэродинамические производные ∂Cx / ∂α, ∂Cy / ∂α (Cy – коэффициент подъемной

силы летательного аппарата), и др., которые, как было сказано,

113