а уравнение неразрывности для несжимаемой жидкости в терминах потенциала скоростей сведется к уравнению Лапласа:

В результате из (3.16) можно определить ϕ и затем из (3.15) рассчитать величину давления p в каждой точке потока.

3.2. Скорость звука

Скоростью звука называют скорость распространения малых возмущений. Понятие скорости звука является одним из важней-

ного цилиндрического объема закон сохранения массы и закон изменения количества движения (см. разд. 2):

Из этих двух уравнений, пренебрегая произведениями малых величин, можно получить v 2 = dpdρ . Очевидно, что для наблюда-

теля, движущегося вместе с жидкостью, жидкость покоится, а возмущение перемещается с такой же скоростью v . Таким образом, v действительно представляет собой скорость распростра-

168

нения звукового фронта или, другими словами, скорость звука, которую далее будем обозначать a . Тогда имеем

Соотношение (3.19) определяет скорость звука через возмущения давления dp и плотности dρ на звуковом фронте. Как

видно из (3.19), скорость звука в несжимаемой среде (dρ = 0 )

равна бесконечности. Конечной величина скорости звука получается только в сжимаемой среде. Опыт показывает, что распространение малых возмущений в газе является адиабатическим процессом. Для совершенного газа имеем интеграл адиабаты в

виде p =Cργ (см. (2.71)). Дифференцируя это соотношение и

подставляя результат в (3.19), получим несколько полезных формул для вычисления скорости звука:

Последняя формула получена с учетом уравнения состояния Клапейрона.

3.3. Различные формы записи уравнения Бернулли

Получим различные формы записи интеграла Бернулли, которые будут полезны в приложениях.

Несжимаемая жидкость. Пусть ρ = const . Функция P в

этом случае имеет вид P = pρ +const. Если в качестве массовых сил выступает только сила тяжести, то Φ = gz . Тогда интеграл Бернулли (3.11) можно переписать в виде

Рассматривая соотношение (3.21) вдоль линии тока и определяя константу в правой части (3.21) по параметрам торможения

– основное уравнение гидравлики несжимаемой жидкости в поле сил тяжести. Индекс 0 в (3.22) соответствует параметрам заторможенного потока. Иногда это уравнение записывают, поделив

мое называют геометрическим напором, второе – пьезометрическим, третье – скоростным. Если в качестве несжимаемой среды рассматривать газ (газ можно считать несжимаемой средой при условии, что сжимаемость не влияет на его параметры, например, в случае движения газа с малыми скоростями, более точно – с малыми числами Маха), то, пренебрегая массовыми силами, которые в задачах аэродинамики, как правило, не играют роли, т.е. полагая Φ = 0 , уравнение Бернулли можно записать так:

смотрению сжимаемого совершенного газа. В этом случае функ-

ция P записывается в виде P = γ γ−1 ρp +const . Пренебрегая си-

лами тяжести (полагая Φ = 0 ), получим из (3.11) уравнение Бернулли:

Используя соотношения из термодинамики (см. подразд. 2.6) и выражение (3.20) для скорости звука, перепишем это уравнение

170

Здесь, как и ранее, индекс 0 соответствует параметрам торможения, "кp" – критическим параметрам, при которых скорость потока равна местной скорости звука, "max" – теоретическому максимальному (предельно возможному) значению скорости течения. Из приведенных уравнений вытекают следующие полезные формулы:

Для дальнейшего практически важно и физически целесообразно ввести безразмерные параметры, определяющие не только количественные характеристики, но и качественные свойства течения сжимаемой среды:

• M =va – число Маха (отношение скорости потока к местной скорости звука);

• M* =v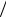aкр – коэффициент скорости или безразмерная

скорость (отношение скорости потока к критической скорости);

• Cr = vvmax – число Крокко (отношение скорости потока

к теоретически максимально возможной скорости).

Эти три безразмерные величины связаны друг с другом. Например, связь числа M* с числом Маха M выражается как

Наиболее распространенным из перечисленных трех параметров является число Маха. В зависимости от его значения можно провести элементарную классификацию газовых течений: при M <1 имеем дозвуковое течение, при M >1 – сверхзвуковое, при M ≈1 – околозвуковое или трансзвуковое. Каждое из этих течений обладает специфическими физическими и математическими особенностями.

171

Используя приведенные выше уравнения, можно получить соотношения, связывающие текущие параметры газового потока с текущим числом Маха:

Эти соотношения также можно рассматривать как различные формы записи уравнения Бернулли. Они очень удобны при прак-

тическом решении задач. Для функций τ(M) , ε(M) и π(M)

составлены подробные таблицы. Из приведенных соотношений легко получить значения так называемых критических парамет-