32

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

фгоувпо «МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра высшей математики и

программного обеспечения ЭВМ

Задания на контрольную работу по темам

«Дифференциальное исчисление функций нескольких переменных.

Дифференциальная геометрия кривых и поверхностей.

Элементы теории скалярного поля. Функции комплексной переменной»

и методические указания к ее выполнению

для студентов 2 курса вечерне-заочного факультета

Мурманск

2007 Г.

Составители:

Кацуба Валентина Сергеевна, канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;

Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;

Демешко Людмила Александровна, ассистент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 30 мая 2007 г., протокол № 7

Рецензент – Котов А.А., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Редактор

Корректор

Мурманский государственный технический университет, 2007

Оглавление

Стр.

Введение 3

Задания на контрольную работу по темам «Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия кривых и поверхностей. Элементы теории скалярного поля. Функции комплексной переменной» 4

Состав теоретического материала и ссылки на литературу 10

Справочный материал к выполнению контрольной работы 11

1.Функции нескольких переменных и ее частные производные 11

1.1. Определение функции нескольких переменных. 11

1.2. Частные производные ФНП. 11

1.3. Полное приращение и полный дифференциал ФНП. 12

1.4. Производные ФНП высших порядков. 13

2. Частные производные ФНП, заданной неявно 14

3. Производная сложной ФНП. Полная производная 14

4. Экстремумы ФНП 15

4.1. Локальные максимумы и минимумы ФНП. 15

4.2 Нахождение наибольшего и наименьшего значений ФНП в замкнутой области 16

5. Касательная плоскость и нормаль к поверхности 16

6. Скалярное поле. Градиент. Производная по направлению 17

7. Функции комплексной переменной 18

7.1. Определение и свойства функции комплексной переменной. 18

7.2. Дифференцирование ФКП. Аналитические ФКП. 20

Решение примерного варианта контрольной работы 22

Рекомендуемая литература 31

Введение

В настоящем пособии содержатся задания к выполнению контрольной работы темам «Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия кривых и поверхностей. Элементы теории скалярного поля. Функции комплексной переменной», а также ссылки на теоретический материал, необходимый для выполнения этой контрольной работы и список рекомендуемой литературы. В результате изучения этих тем студенты должны:

• знать основные понятия теории дифференциального исчисления функций нескольких переменных (область определения, частные производные, частные и полное приращения, полный дифференциал и др.);

• уметь находить частные производные для явно и неявно заданной функций нескольких переменных;

• уметь находить частные и полную производные для сложной функции нескольких переменных;

• уметь находить глобальные экстремумы функции двух переменных в замкнутой области;

• иметь представление об основных поверхностях 2-го порядка, уметь находить уравнения касательной плоскости и нормали к поверхности;

• знать основные понятия теории скалярного поля и уметь определять его основные характеристики;

• иметь представление о функции комплексной переменной, об ее аналитичности и уметь дифференцировать аналитические функции комплексной переменной.

Данные методические рекомендации включают также справочный материал, необходимый для выполнения контрольной работы по теме «Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия кривых и поверхностей. Элементы теории скалярного поля. Функции комплексной переменной» и решение примерного варианта работы, в котором имеются ссылки на используемый справочный материал.

Задания на контрольную работу по темам «Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия кривых и поверхностей. Элементы теории скалярного поля. Функции комплексной переменной»

Контрольная работа состоит из семи задач. Задание для каждой задачи включает в себя ее формулировку и десять вариантов исходных данных.

Перед выполнением контрольной работы необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии со ссылками на литературу, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы.

Задача 1. Дана функция z = f(x,y). Требуется:

1) найти частные производные и ;

2) найти полный дифференциал dz;

3) показать, что для данной функции справедливо равенство: .

Номер варианта	Функция	Номер варианта	Функция
1	z = ln(+ 2 y3)	2	z = (y2 – x) arcsin(2x)
3	z = tg(x – 5 y2)	4	z = (y + 4x)2
5	z = + cos(x y)	6	z = ln3 (2y – x)
7	z = x cos(3x + 2y)	8	z =
9	z =x y + sin(x – y)	10	z = 4xy5 –

Задача 2. Найти частные производные ,и, если переменныеx, y, и z связаны равенством вида .

Номер варианта	Равенство	Номер варианта	Равенство
1	+ 3x2 siny – 2 x z3 = 0	2	sin(x y2) + z3 x y2 + z4 – x = 0
3	x+z y + y2 lnx – 2z = 0	4	(x – 2y)4 – 5+ 3cosx – z5 =0
5	ln(x z3) + y3 – 5x2y z4 + 5x = 0	6	cos(y + ez)+ x z5 y + 3x3 + 4 = 0
7	+ y tgx – z x5 + 3y = 0	8	(z – 2x)3+3y4 x – y2e2z –2 x = 0
9	z ++ y2 z x – y5 = 0	10	sin2z + ln(x –y)+ 2x4 – 3yz2 = 0

Задача 3. Дана сложная функция z= f (x, y, t), где . Найти полную производную.

Номер варианта	Функция z= f (x, y, t)	Функции
1	u = (3t + 2x2 – y)3	x = tgt, y =
2	u = (4t – x)	x = ,y =
3	u = tsin(x3 + y)	x = + 1,y = t4
4	u = tg(x + t )	x = ln(t3+ 1), y = t2
5	u =	x = sin3t, y = 1 – 5t
6	u= sin(x2 + y) – y	x = ,y =
7	u =	x = cos4t, y = sin2t
8	u = xctg(t – 3y)	x = 2 – 3t2, y =
9	u = ln(2t + x – y2)	x = sin2t, y =3t –
10	u = xy2 + cos(y + 2t)	x = –t, y =2t – 4

Задача 4. Дана функция и уравнения границ замкнутой области D на плоскости XОY. Требуется:

1) найти наибольшее и наименьшее значения функции в области D;

2) сделать чертеж области D в системе координат, указав на нем точки, в которых функция имеет наибольшее и наименьшее значения.

Номер варианта	Функция	Уравнения границ области D
1	z = x2 – xy + 2y2 + 3x + 2y +1	x = 0, y = 0, x + y = –5
2	z = x2 + y2 – 6x + 4y + 2	x = 1, y = –3, x + y = 2
3	z = 5x2 – 3xy + y2 + 5x + 4	x = –1, y = –1, x + y = 1
4	z = x2 – 2y2+ 4xy – 6x – 1	x = 1, y = 0, x + y = 3
5	z = x2 – 3xy + 4x + 8y	x = 0, y =1, x + y = –2
6	z = x2 – 4xy + 3y2 + x – y	x = 1, y = 1, y + x = 5
7	z = 10 + 6x + 2xy – x2	x = – 3, y = – 1, x + y = 0
8	z = 2x2 + y2 + xy – x + y + 3	x = –1, y = 2, x – y = 0
9	z = x2 + y2 – xy – 4x + 1	x = 0, y = 0, x + y = 4
10	z = x2 + y2 – xy + x + y	x = –1, y = 2, x + y = –3

Задача 5. Поверхность σ задана уравнением . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀, y₀ – заданные числа.

Номер варианта	Уравнение поверхности	Значения x0, y0
1	z = 3y – x2y + x	x0 = 1, y0 = 5
2	z = + 3x – y2	x0 = 1, y0 = –1
3	z = +x3 – 5	x0 = 1, y0 = 4
4	z = y3x – y + x2	x0 = –1, y0 = 2
5	z = cosy + 2x2 – xy	x0 = 2, y0 = 0
6	z = xy + y3 + 2x	x0 = 2, y0 = 1
7	z = ln(2x) – xy3 + y	x0 = ,y0 = 2
8	z = + x2y – x4 + 1	x0 = –1, y0 = 0
9	z = ysinx + 3y2	x0 = ,y0 = –1
10	z = 2y – +x5	x0 = 1, y0 = 3

Задача 6. Дано плоское скалярное поле , точкаM₀(x₀, y₀) и вектор . Требуется:

1) найти уравнения линий уровня поля;

2) найти градиент поля в точке M₀ и производную в точке M₀ по направлению вектора ;

3) построить в системе координат XОY 4-5 линий уровня, в том числе линию, проходящую через точку M₀, изобразить вектор на этом чертеже.

Номер варианта	Скалярное поле	Точка M0 (x0, y0)	Вектор
1	U = x2 + 3y2	M0(1, 1)	= 3– 4
2	U = x2 – 2 y2	M0(2, 1)	= 6+ 8
3	U = –3y – x2	M0(–1, –1)	= + 2
4	U = y2 – 4x	M0(–2, 1)	= –2+ 2
5	U = 2x2 – y2	M0(1, 1)	= –– 3
6	U = 2 x2 + y2	M0(1, 2)	= 2+ 2
7	U = x3 – y	M0(1, –2)	= –2+
8	U =2x + y2	M0(–2, 1)	= +
9	U = (x + 1)2 + y2	M0(0, 2)	= – 2
10	U = 3x2 – y2	M0(1, –1)	= –2+ 3

Задача 7. Дана функция комплексной переменной , гдеи точкаz₀. Требуется:

1. представить в виде 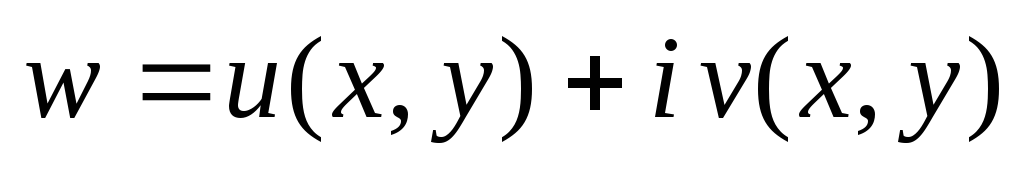, разделив ее вещественную и мнимую части;

2. проверить, является ли функция w аналитической;

3. в случае аналитичности функции w найти ее производную в точке z₀.

№ варианта	Функция , точка z0	№ варианта	Функция , точка z0
1		6
2		7
3		8
4		9
5		10