
- •А л г е б р а
- •Глава 1. Системы линейных уравнений и арифметическое векторное пространство. §1. Системы линейных уравнений и их решение методом Гаусса.
- •§2. Арифметическоеn-мерное векторное пространство. Линейная зависимость и независимость. Базис и ранг системы векторов.
- •§3. Однородная система линейных уравнений. Фундаментальный набор решений.
- •Глава 2. Матрицы и определители. §4. Алгебра матриц.
- •§5. Определитель квадратной матрицы.
- •Глава 3. Комплексные числа. §6. Поле комплексных чисел.
- •§7. Уравнения третьей степени.
- •§8. Уравнения четвёртой степени.
- •Литература.
- •На молдавском языке.
Глава 3. Комплексные числа. §6. Поле комплексных чисел.
Мнимая единица. Алгебраическая и тригонометрическая формы записи комплексного числа. Равенство комплексных чисел. Арифметические операции над комплексными числами и их геометрическая интерпретация. Комплексная плоскость и формула Муавра. Извлечение корня из комплексного числа. Двучленные уравнения.
Поле комплексных чисел С– это расширение поля действительных чисел, полученное присоединением корняi(мнимая единица), квадратного уравненияx2+1=0. Элементы поляСназываюткомплексными числами. Причём,
С== a+bi,aR,bR
Представление комплексного числа в виде a+biединственно, т.е.
a+bi = с+di (a=c
иb=d),
=a+bi
– алгебраическая форма записи
комплексного числа. Действительные
числаa,bназываются соответственнодействительной частью и коэффициентом
при мнимой части числа.
Во множестве комплексных чисел определенаоперация сопряжения, однозначно
сопоставляющая каждому числу=a+biсопряжённое с ним число![]() =a–bi.
=a–bi.
Простейшие
свойства операции сопряжения:
1)![]() =;2)
=;2) ![]() =R;3)
=R;3)![]() =
=![]() ;4)
;4)![]() =
=![]() ;5)
;5)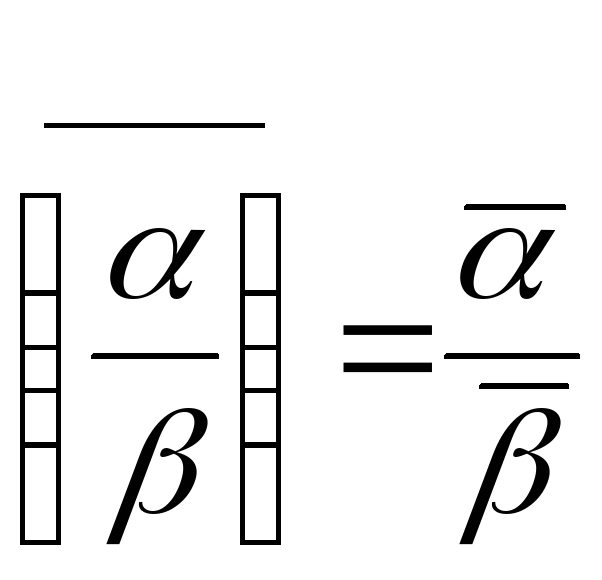 ,
при0;6)(+
,
при0;6)(+![]() )R;7).
)R;7).![]() R8)если0, то
R8)если0, то![]() .>0.
.>0.
Операции сложения,
вычитания, умножения и деления комплексных
чисел = a+biи=с+diопределяются
правилами:+=(a+bi)+(с+di)=(a+c)+(b+d)i;–=(a+bi)–(с+di)=(a–c)+(b–d)i;.=(a+bi).(с+di)=(ac–bd)+(ad+bc)i;![]() (деление
определено, если0).
(деление
определено, если0).
К аждое
комплексное число=a+biопределяет пару (a,b)
действительных чисел, которой на
координатной плоскости соответствует
точка М с координатами (a,b) или
радиус-вектор
аждое
комплексное число=a+biопределяет пару (a,b)
действительных чисел, которой на
координатной плоскости соответствует
точка М с координатами (a,b) или
радиус-вектор![]() .
Указанные соответствия взаимно
однозначны. Этот факт позволяет
представлять числа как точки координатной
плоскости, или как радиус-векторы.
Сложение, вычитание комплексных чисел
можно представить как сложение
(вычитание) соответствующих векторов.
.
Указанные соответствия взаимно
однозначны. Этот факт позволяет
представлять числа как точки координатной
плоскости, или как радиус-векторы.
Сложение, вычитание комплексных чисел
можно представить как сложение
(вычитание) соответствующих векторов.
На плоскости можно использовать не только декартову xOy,но и полярную систему координатOx(рис.1), в которой a= r.cos, b=r.sin, тогда=a+bi= r.(cos+i.sin).
Запись числа в виде r.(cos+i.sin)
называетсятригонометрической формой
комплексного числа. Длина вектора![]() ,
изображающего число=a+bi,
называется модулем этого комплексного
числа:
,
изображающего число=a+bi,
называется модулем этого комплексного
числа:
r==![]()
Угол, который
образует вектор
![]() ,
с положительным направлением оси Ox
, называетсяаргументом комплексного
числа0:
arg=,
,
с положительным направлением оси Ox
, называетсяаргументом комплексного
числа0:
arg=,
![]() =cos,
=cos,![]() =sin.
=sin.
Полярные координаты точки, в отличие от декартовых, определяются неоднозначно: если r1.(cos1+i.sin1)= r2.(cos2+i.sin2), то r1=r2и1=2+2k, где kZ.
В тригонометрической форме над комплексными числами удобно выполнять действия умножения, деления, возведения в степень и извлечения корней натуральной степени: если 1=r1.(cos1+i.sin1),2=r2.(cos2+i.sin2), то
![]() (cos(j1–2)+i.sin(j1–2));
(cos(j1–2)+i.sin(j1–2));
1.2=r1.r2(cos(j1+2)+i.sin(j1+2));
()n=rn(cos(n)+
i.sin(n));
![]() =.(cos+i.sin),
где =
=.(cos+i.sin),
где =![]() ,
=
,
=![]() ,
k=0..(n–1).
,
k=0..(n–1).
При умножении комплексных чисел их модули перемножаются, а аргументы складываются, поэтому умножение на комплексное число с модулем, равным 1, геометрически можно интерпретировать как поворот на угол argвокруг начала координат, т.е. соответствие(или функция f=) при=1 задаёт преобразование комплексной плоскости, именно указанный поворот.
Параллельный перенос на вектор, определяемый комплексным числом ,описывается функцией f=+. Умножение числана комплексное число сводится к растяжению вектора, изображающего, враз и повороту на угол=argвокруг начала координат. Функция f=+,,С,1, задаёт на комплексной плоскости гомотетию с центром в точке/(1–), коэффициентом k=и поворот с этим центром на угол=arg, что следует из равенства:
+=(–/(1–))+/(1–);
При извлечении
корня n-ной степени из числа все его n значений имеют одинаковые
модули, а аргументы различаются на
углы, кратные 2/n.
Таким образом, все значения![]() располагаются на окружности радиусом
располагаются на окружности радиусом![]() с
центром в начале координат через угол
2/n.
с
центром в начале координат через угол
2/n.
Множество всех
корней n-ой степени из числа можно получить умножением одного
из этих корней на все значения![]() .
.
Используя формулу Эйлера
![]() =cos+i.sin,
всякое
комплексное число можно представить
в виде:
=cos+i.sin,
всякое
комплексное число можно представить
в виде:
=![]()
Образцы решения задач.
Задача 1. Вычислить: 1) (2+3i)+(5–7i); 2) (4+i)–(7+2i); 3) (3+2i)(5–2i); 4) (2+i)/(1+3i).
Решение.
Пользуясь обычными свойствами действий:
коммутативностью, ассоциативностью,
дистрибутивностью, получим:
1)
(2+3i)+(5–7i)=(2+5)+(3–7i)= 7–4i;
2)
(4+i)–(7+2i)=(4–7)+(1–2)i=–3–i;
3)
(3+2i)(5–2i)=35+2i5–32i–(2i)2=15+10i–6i–4(–1)=
19+4i; (i2=–1);
4)![]() =
=![]() =
=![]() =
=![]() =
=![]() .
.
Ответ:
1) 7–4i; 2) –3–i; 3) 19+4i; 4) ![]() .
.
Задача 2. Найти действительные корни уравнения: (2+i)x+(1–i)y=5–2i.
Решение.
Преобразуем левую часть уравнения,
следующим образом:
(2x+y)+(x–y)i=5–2i.
Учитывая единственность представления
комплексного числа и то, что x,yR,
имеем![]() ∆=
∆=![]() =–3;
∆1=
=–3;
∆1=![]() =-3;
∆2=
=-3;
∆2=![]() =–9.
Откуда
x=∆1/∆=1; y=∆2/∆=3.
=–9.
Откуда
x=∆1/∆=1; y=∆2/∆=3.
Ответ: (1;3).
Задача 3.
Вычислить![]()
Решение. Пусть– искомое число.
Тогда по определению квадратного корня
4+3i =2. Если=
х+yi, x,yR, то
4+3i=(х+yi)2или 4+3i=(x2–y2)+2xyi
Откуда,
т.к. x,yR, получим![]() (1)
Возведя
в квадрат оба уравнения системы (1), и
сложив их, выведем следствие системы
(1):
x2+2x2y2+y2=25, (2)
которое
преобразуется к виду (x2+y2)2=25.
Поэтому на множестве пар действительных
чисел уравнение (2) равносильно уравнению
(3):
x2+y2=5 (3)
Если в систему
уравнений включить её следствие, то
получится система, равносильная
исходной. Включим уравнение (3) в систему
(1):
(1)
Возведя
в квадрат оба уравнения системы (1), и
сложив их, выведем следствие системы
(1):
x2+2x2y2+y2=25, (2)
которое
преобразуется к виду (x2+y2)2=25.
Поэтому на множестве пар действительных
чисел уравнение (2) равносильно уравнению
(3):
x2+y2=5 (3)
Если в систему
уравнений включить её следствие, то
получится система, равносильная
исходной. Включим уравнение (3) в систему
(1):
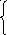
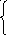
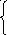 x2+y2=5 2x2=9x2=9/2x2–y2=52y2=5y2=1/2
2xy=3 2xy=3xy=3/2
x2+y2=5 2x2=9x2=9/2x2–y2=52y2=5y2=1/2
2xy=3 2xy=3xy=3/2
Итак, система (1)
имеет два решения:
![]() и
и![]() .
Они дают два значения корня:1=
.
Они дают два значения корня:1=![]() ,2=
,2=![]() .
.
Ответ:![]() =
=![]() .
.
Задача 4. Решить уравнение: x2–(2+i)x+(–1+7i)=0
Решение.
Воспользуемся формулой вычисления
корней квадратного уравнения
x1,2=![]() ,
откуда
x1=3–i, x2=–1+2i.
,
откуда
x1=3–i, x2=–1+2i.
Ответ. 3–i; –1+2i.
Замечание. Квадратный корень из числа 7–24i извлекается как в задаче 3.
Задача 5. Вычислить in, где nZ.
Решение. Вычислим inдля нескольких натуральных показателей: i0=1 (по определению), i1=i, i2=–1, i3=–i, i4=1, i5=i. Замечаем, что значения степени начинают повторяться: i4=i0, i5=i1, i6=i2, i7=i3,….Обобщим это наблюдение. Возьмём произвольное целое число n и поделим его с остатком на 4:
n=4k+r,
k,rZ,
0r<4.
Тогда
in=i4k+r=(i4)kir=
ir,
так как
i4=1.
Значения irдля 0r<4
уже найдены. Итак,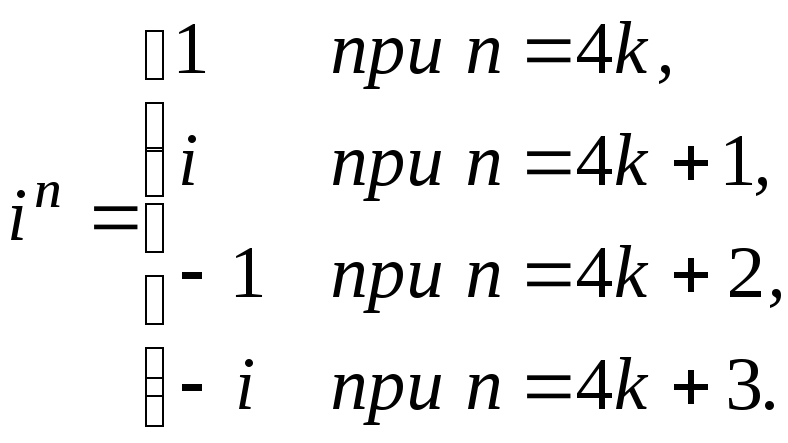
Задача 6. Решить систему уравнений
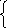 (2+i)x–(3–i)y=i
(3+i)x+(2–i)y=i.
(2+i)x–(3–i)y=i
(3+i)x+(2–i)y=i.
Решение.
Вычислим основной и два вспомогательных
определителя
системы:
∆=![]() =(2+i)(2–i)+(3+i)2=13+6i;
∆1=
=(2+i)(2–i)+(3+i)2=13+6i;
∆1=![]() =i(2–i)+i(3+i)=2i+1+3i–1=5i;
∆2=
=i(2–i)+i(3+i)=2i+1+3i–1=5i;
∆2=![]() =2i–1–3i+1=–i.
Тогда
x=∆1/∆=
=2i–1–3i+1=–i.
Тогда
x=∆1/∆=![]() ;
y=∆2/∆=
;
y=∆2/∆=![]()
Ответ:![]() ;
;![]() .
.
Задача 7.
Представить в тригонометрической
форме:
1)![]() ;
2)–7i 3) 1+cos+isin.
;
2)–7i 3) 1+cos+isin.
Решение.
1 )
Найдём модуль r и аргументданного числа:
r=
)
Найдём модуль r и аргументданного числа:
r=![]() ;
tg=
;
tg=![]() (=–/3
или=2/3).
Таким образом,
(=–/3
или=2/3).
Таким образом,![]() =2(cos
=2(cos![]() +isin
+isin![]() ).
).
2) На комплексной
плоскости число (–7i) изображается
радиус–вектором
![]() =(0;–7).
Тогда
–7i=
=(0;–7).
Тогда
–7i=![]() =7,
arg(–7i)=XOM=–/2.
Итак,
(–7i)=
7(cos(–/2)+isin(–/2)).
=7,
arg(–7i)=XOM=–/2.
Итак,
(–7i)=
7(cos(–/2)+isin(–/2)).
3) Преобразуем данное число: 1+cos+isin=2cos2(/2)+i[2sin(/2)cos(/2)]= =2cos(/2)[cos(/2)+isin(/2)]. Если cos(/2)>0, то это и есть искомая тригонометрическая форма. Если же cos(/2)<0, то внесём (–1) внутрь скобок: 2cos(/2)[cos(/2)+isin(/2)]=–2cos(/2)[cos(/2+)+isin(/2+)]
Ответ:
1) ![]() =2(cos
=2(cos![]() +isin
+isin![]() );
2)–7i=7(cos(–/2)+isin(–/2));
3) 1+cos+isin=
);
2)–7i=7(cos(–/2)+isin(–/2));
3) 1+cos+isin=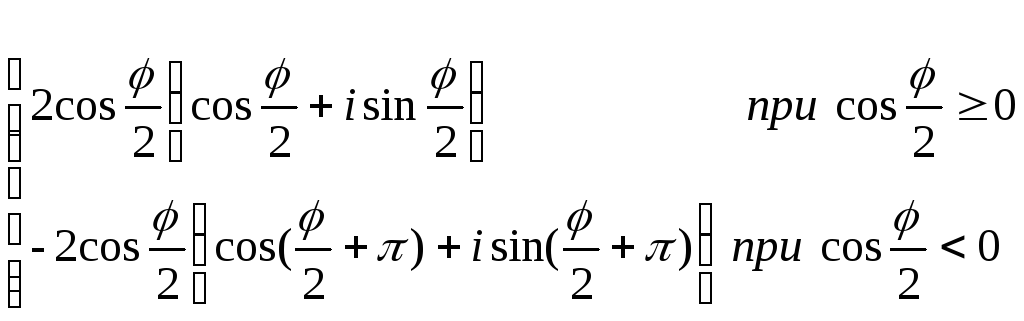 .
.
Задача 8.
Вычислить:
1)![]() ;
2)
;
2)![]() ;
;
Решение.
1) Представим
числа, стоящие в числителе и знаменателе
дроби в тригонометрической форме,
для этого найдём модули и аргументы
числителя и знаменателя.
=![]() ,=
,=![]() =2,
arg=–/3
(см. задачу 7, п.1).=1+i,=
=2,
arg=–/3
(см. задачу 7, п.1).=1+i,=![]() =
=![]() ,
arg=/4.
Выполняя
операцию деления, получим:/=
,
arg=/4.
Выполняя
операцию деления, получим:/= =
=![]() .
К
полученному выражению применим формулу
возведения тригонометрической формы
комплексного числа в степень (формулу
Муавра):
.
К
полученному выражению применим формулу
возведения тригонометрической формы
комплексного числа в степень (формулу
Муавра):![]() =
=
=
=![]() =
=
=
=![]() =
=
=
=![]() =
=![]() .Замечание1. Запись вычислений можно вести так:
.Замечание1. Запись вычислений можно вести так:![]() =
=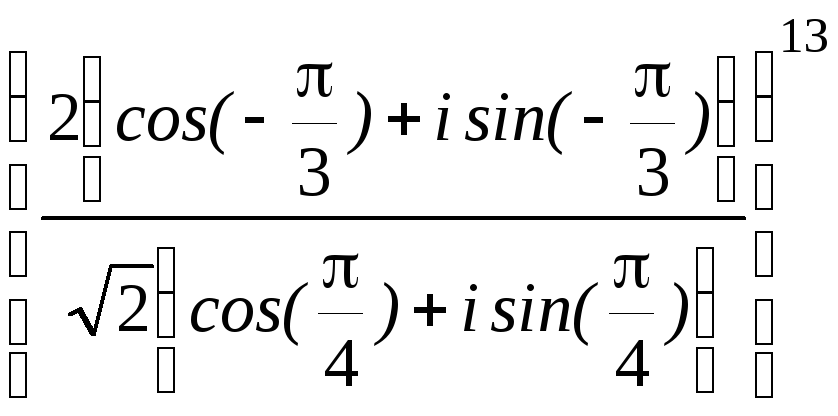 =
=![]() =
=
=
=![]() =
=
=
=![]() =
=![]() .
.
2). Задачу можно
решить в алгебраической форме.
![]() =
=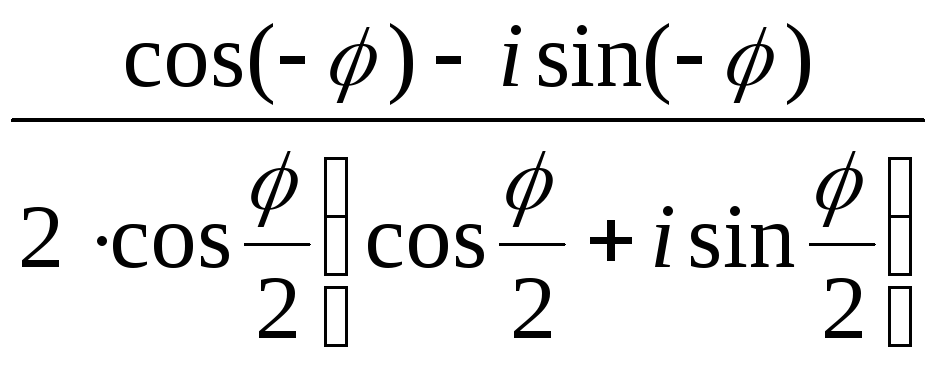 =
=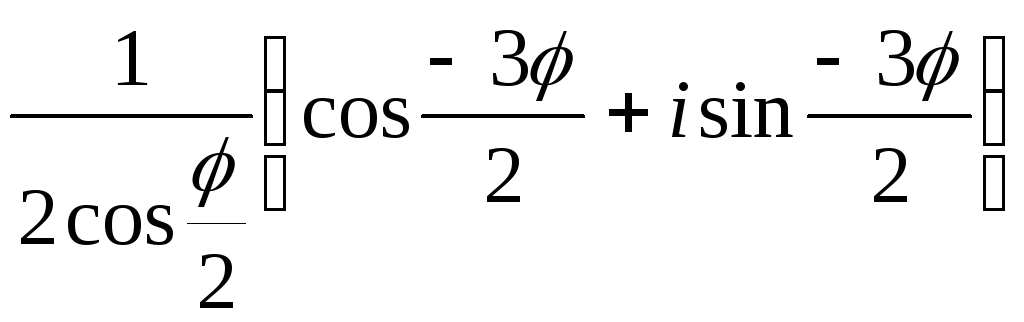 Замечание.
1) Используем результат задачи 7, п.3.
2)
Знак сos(/2) может
быть любым, так как результат не
обязательно получать в тригонометрической
форме.
3) Ответ можно записать и так:
Замечание.
1) Используем результат задачи 7, п.3.
2)
Знак сos(/2) может
быть любым, так как результат не
обязательно получать в тригонометрической
форме.
3) Ответ можно записать и так: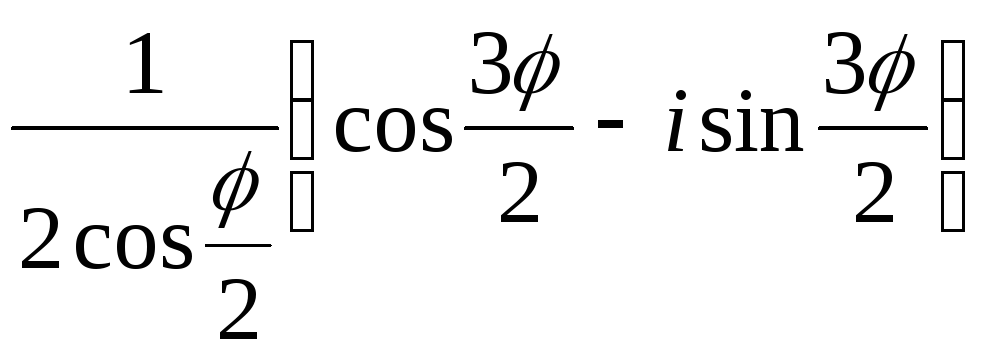 .
.
Ответ: 1)![]() =
=![]() ;
2)
;
2)![]() =
=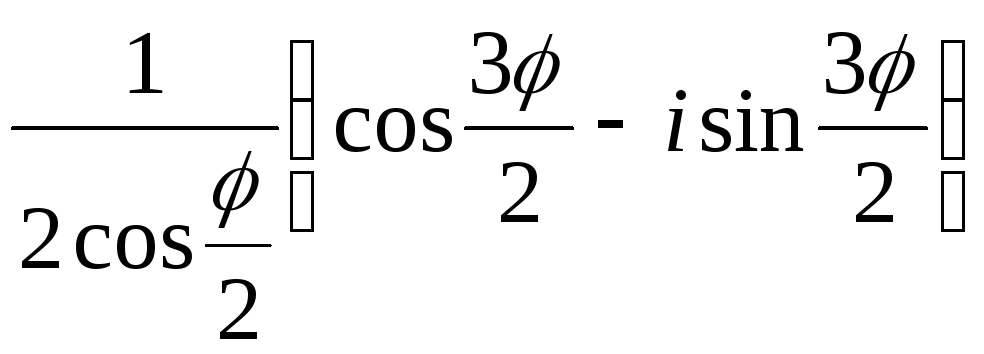 .
.
Задача 9. Найти
все корни:
1) 5-ой степени из=![]() ;
2)
6-ой степени из 1+cos+isin;
3)
3-тей степени из i.
;
2)
6-ой степени из 1+cos+isin;
3)
3-тей степени из i.
Решение. 1)
Запишемв
тригонометрической форме:=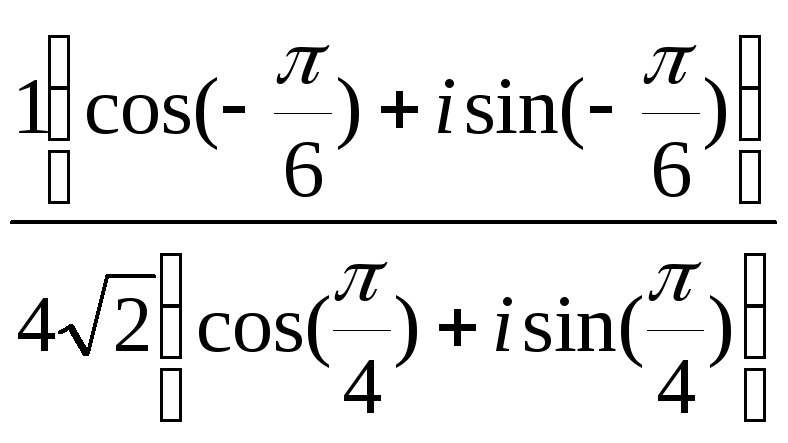 =
=![]() .
Воспользуемся
формулой извлечения корня n-ой степени
из тригонометрической формы комплексного
числа:k=
.
Воспользуемся
формулой извлечения корня n-ой степени
из тригонометрической формы комплексного
числа:k=![]() ,
k=0..4.
Найдём
,
k=0..4.
Найдём![]() ,
,![]() .
Все
искомые корни задаются формулойk=
.
Все
искомые корни задаются формулойk=![]() ,
k=0..4.
,
k=0..4.
2) Воспользуемся
результатом задачи 7, п.3. В данном случае,
чтобы можно было воспользоваться
формулой, необходима тригонометрическая
форма подкоренного выражения
(арифметический корень по определению
существует только из положительного
числа). Ответ получаем сразу:
k= ,
,![]() k=0..5,=0 при
k=0..5,=0 при![]() .
.
3 )
В качестве значения arg i выбираем то,
которое делится на 3: из рис. 3
arg=–3/2.
Так какi=1,
то одним из искомых корней будет:0=cos(–/2)+isin(–/2)=–i.
Остальные корни найдём, умножая0на корни 3-й степени из 1, т.е. наk=
)
В качестве значения arg i выбираем то,
которое делится на 3: из рис. 3
arg=–3/2.
Так какi=1,
то одним из искомых корней будет:0=cos(–/2)+isin(–/2)=–i.
Остальные корни найдём, умножая0на корни 3-й степени из 1, т.е. наk=![]() ,
k=0..2. Найдём
,
k=0..2. Найдём![]() :0=
:0=![]() =1;1=
=1;1=![]() =
=![]() ;2=
;2=![]() =
=
=
=![]() .
Тогдаk=k0,
т.е.0=–i,
1=
.
Тогдаk=k0,
т.е.0=–i,
1=![]() ,
2=
,
2=![]() .
.
Ответ.
1) k=![]() ,
k=1..4;
2) k
=
,
k=1..4;
2) k
=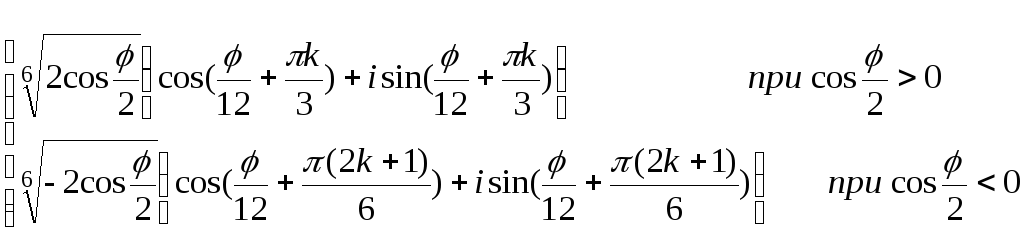 ;k=0..5,
=0,
при
;k=0..5,
=0,
при ![]() .
.
3)
0=–i,
1=![]() ,
2=
,
2=![]() .
.
Задача 10. Решить уравнения: 1) x9+8=0; 2) x6+4x3+8=0.
Решение. 1)
x9+8=0x9=–8.
Корнями этого уравнения являются корни
9-той степени из (–8) и только они. Один
из них равен![]() ,
все остальные корни получим, домножая
его на все корни 9-ой степени из
1:k=0k=
,
все остальные корни получим, домножая
его на все корни 9-ой степени из
1:k=0k=![]() ,
k=0..8.
,
k=0..8.
2) Используем
подстановку y=x3, тогда уравнение
примет вид:
y2+4y+8=0.
Корни
квадратного уравнения
y1,2=–2![]() =–22i=2
=–22i=2![]() (
(![]() )
Извлекая
кубический корень, получим ответ:
x1..6=
)
Извлекая
кубический корень, получим ответ:
x1..6=![]()
![]() ,
k=0..2.
,
k=0..2.
Замечание.
Уравнение n-ой степени в поле комплексных
чисел имеет в точности n решений
(некоторые из которых могут совпадать).
Поэтому указанное уравнение 6-ой степени
имеет в точности 6 решений. Корни из
числа cos–isinсопряжены с корнями из числа cos+isin, т.е. в формуле для корней нужно заменить
i на (–i). Извлекать корни из y можно так:
один из корней0=![]()
![]() =
=![]()
![]() =1+i;
умножая его на корни 3-тей степени из
единицы, получаем:
(1+i)
=1+i;
умножая его на корни 3-тей степени из
единицы, получаем:
(1+i)![]()
![]() .
Аналогично
находим остальные значения x. Окончательно
получим:
x1,2= 1i,
x3,4=
.
Аналогично
находим остальные значения x. Окончательно
получим:
x1,2= 1i,
x3,4=![]() ,
x5,6=
,
x5,6=![]() .
.
Ответ: 1) xk=![]() ,
k=0..8.2) x1,2=
1i,
x3,4=
,
k=0..8.2) x1,2=
1i,
x3,4=![]() ,
x5,6=
,
x5,6=![]() .
.
Для самостоятельного решения.
1)
Вычислить: а)
(3–2i)2+(1+3i)(–2+5i);
б)
(2+3i)(4–5i)–(2–3i)(4+5i);
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
.
2) Решить уравнения: а) x2–(2+i)x–1+7i=0; б)x2–(3–2i)x+5–5i=0; в)x4–3x2+4=0.
3) Представить в
тригонометрической форме:
а) 2–2i; б)
–3–i![]() ;
в) 5; г) –4; д) 3i.
;
в) 5; г) –4; д) 3i.
4) Вычислить
а)
![]() б)
б)![]() в)
в)![]()
5) Решить уравнения: а) x6+27=0; б)x8+x4+1=0.
