
- •А л г е б р а
- •Глава 1. Системы линейных уравнений и арифметическое векторное пространство. §1. Системы линейных уравнений и их решение методом Гаусса.
- •§2. Арифметическоеn-мерное векторное пространство. Линейная зависимость и независимость. Базис и ранг системы векторов.
- •§3. Однородная система линейных уравнений. Фундаментальный набор решений.
- •Глава 2. Матрицы и определители. §4. Алгебра матриц.
- •§5. Определитель квадратной матрицы.
- •Глава 3. Комплексные числа. §6. Поле комплексных чисел.
- •§7. Уравнения третьей степени.
- •§8. Уравнения четвёртой степени.
- •Литература.
- •На молдавском языке.
Глава 2. Матрицы и определители. §4. Алгебра матриц.
Операции над матрицами. Обратная матрица. Матричное уравнение АХ=В. Система линейных уравнений как матричное уравнение.
Операции сложения, умножения транспонирования матриц, умножение матрицы на число. Матричное уравнение. Единичная матрица, обратная матрица. Вычисление обратной матрицы с помощью элементарных преобразований. Теоремы о ранге произведения матриц.
Пусть Р–
некоторое поле (поле скаляров). Матрицы,
составленные из элементов этого
поля, будемназывать матрицами
порядка m![]() n,
гдеmиnнатуральные числа указывающие число
строк и столбцов соответственно.
Обозначать матрицу будем так:
n,
гдеmиnнатуральные числа указывающие число
строк и столбцов соответственно.
Обозначать матрицу будем так:
A=![]() =
=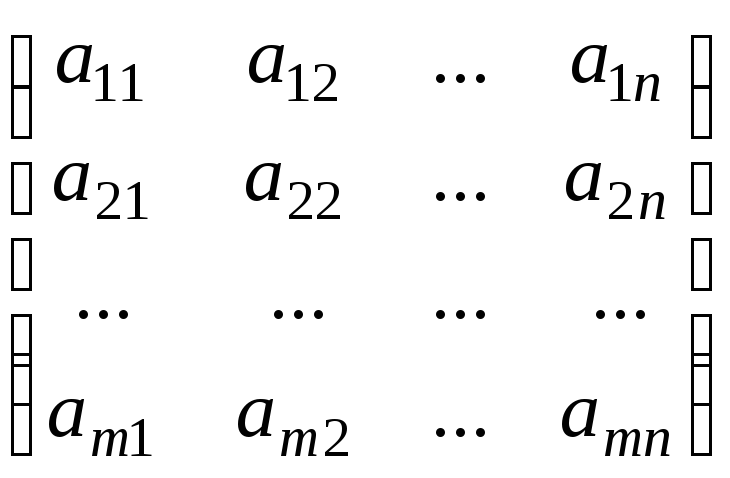
Если m=nто матрицуАназываютквадратной
матрицейпорядкаn.
Обозначимi-ю строку
матрицыАчерезА![]() :
:
A![]() =
=![]() ,
,
а j-й столбец матрицы А – через Аj
Aj=![]()
Две матрицы
порядка
![]()
![]() =
=![]() и
и![]() называютравнымии пишут
называютравнымии пишут![]() ,
если
,
если![]() =
=![]() для любых наборовi,jгде
для любых наборовi,jгде![]() =1..n,j=1..m.
=1..n,j=1..m.
Матрица называется нулевой, если все ее элементы равны нулю.
Суммой двух
матриц A и
Bпорядкаm![]() nназывается матрицаCпорядкаm
nназывается матрицаCпорядкаm![]() n,
элемент
n,
элемент![]() который равен
который равен![]() ,
т.e.
,
т.e.
![]() =
=![]() =
=![]()
Произведением
матрицы A=![]() порядка
порядка![]() на число (скаляр)
на число (скаляр)![]()
![]() называется матрицаDпорядка
называется матрицаDпорядка![]() ,
элемент
,
элемент![]() который равен
который равен![]() ,
т.e.
,
т.e.
![]()
Нетрудно увидеть,
что операции сложения матриц,
умножения матрицы на скаляр
обобщают аналогичные операции над
арифметическими векторами (которые
являются матрицами порядка
![]() )
и обладают свойствами 1–8 (см §
)
и обладают свойствами 1–8 (см §![]() ).
).
Рассмотрим матрицу
![]() порядка
порядка![]() и матрицу
и матрицу![]()
![]() порядка
порядка![]() .
Произведение строки
.
Произведение строки![]() на столбец
на столбец![]() определим следующим образом:
определим следующим образом:
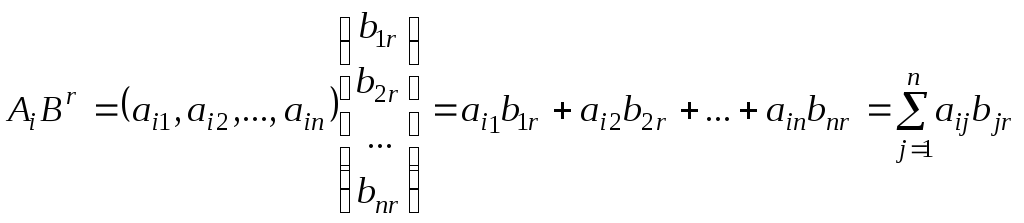
Произведением
матриц
![]() и B называется матрица
и B называется матрица![]() порядка
порядка![]() ,
такая, что,
,
такая, что,![]() или
или
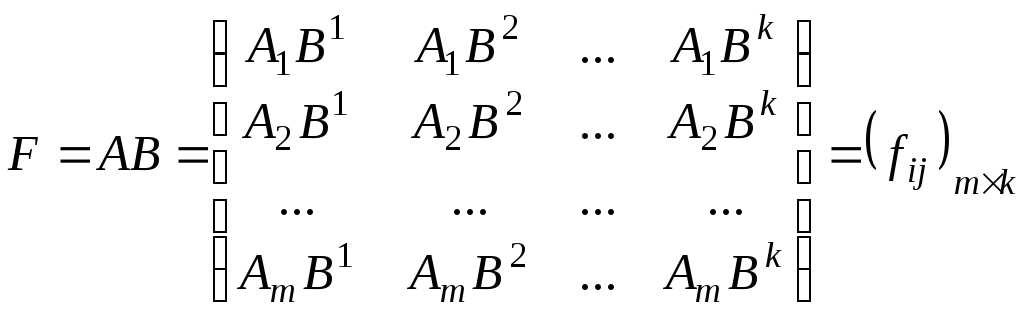
Согласно
определению произведения матриц
![]() и
и![]() у матрицы
у матрицы![]() число строк совпадает с числом
столбцов матрицы
число строк совпадает с числом
столбцов матрицы![]() ,
а число столбцов – с числом
столбцов матрицы
,
а число столбцов – с числом
столбцов матрицы![]() ,
т.e. если
,
т.e. если![]() – матрица порядка
– матрица порядка![]() ,
аB – матрица
порядка
,
аB – матрица
порядка![]() ,
то
,
то![]() –
матрица порядка
–
матрица порядка![]() .
При этом
.
При этом![]()
Непосредственный
анализ определения операции умножения
матриц показывает, что каждый столбец
произведения матриц АиВлинейно выражается через систему
столбцов матрицы![]() ,
а каждая строка этого произведения
линейно выражается через систему
срок матрицы
,
а каждая строка этого произведения
линейно выражается через систему
срок матрицы![]() .
Или более подробно:
.
Или более подробно:![]() -ый
столбец матрицы
-ый
столбец матрицы![]() есть линейная комбинация всех
столбцов матрицы
есть линейная комбинация всех
столбцов матрицы![]() ,
коэффициенты этой комбинации –
элементы
,
коэффициенты этой комбинации –
элементы![]() -го
столбца матрицы
-го
столбца матрицы![]() ,
,![]() -ая
строка матрицыABесть линейная комбинация всех строк
матрицы
-ая
строка матрицыABесть линейная комбинация всех строк
матрицы![]() ,
а коэффициенты этой линейной
комбинации – элементы
,
а коэффициенты этой линейной
комбинации – элементы![]() -ой
строки матрицы
-ой
строки матрицы![]() .
Эти утверждения лежат в основе
доказательствапервой теоремы
о ранге произведения матриц:ранг
произведения матриц не превосходит
ранга каждого из сомножителей :
.
Эти утверждения лежат в основе
доказательствапервой теоремы
о ранге произведения матриц:ранг
произведения матриц не превосходит
ранга каждого из сомножителей :
![]()
Умножение матриц
не коммутативно, например:
![]()
![]() =
=![]() =
=![]()
![]()
![]() =
=![]() =
=![]()
Если же
![]() ,
то матрицы
,
то матрицы![]() называютперестановочными.
называютперестановочными.![]()
Умножение матриц
ассоциативно: если существуют
произведения![]() и
и![]() матриц, то существуют также и
произведения
матриц, то существуют также и
произведения![]() и
и![]() ,
и они равны:
,
и они равны:
![]() .
.
Отметим также,
что
![]() если
произведениеABсуществует.
Умножение матриц связано со сложением
двумядистрибутивными законами:
если существуют матрицыA+BиACто существуют
также
если
произведениеABсуществует.
Умножение матриц связано со сложением
двумядистрибутивными законами:
если существуют матрицыA+BиACто существуют
также![]() ,
,![]() и
и![]() (правый
дистрибутивный закон);если
существуют
(правый
дистрибутивный закон);если
существуют![]() и
и![]() то существуют и
то существуют и![]() и
и![]() (левый дистрибутивный закон).
(левый дистрибутивный закон).
Транспонированием
матрицы называют замену ее строк
столбцами с сохранением порядка
их записи, т.e. если![]() – матрица порядка
– матрица порядка![]() то транспонированная матрица
то транспонированная матрица![]() – порядка
– порядка![]() .
Очевидно, что если
.
Очевидно, что если![]() и
и![]() существуют, то существуют также
существуют, то существуют также![]() и
и![]() ,
и
,
и![]()
Рассмотрим
систему
![]() линейных уравнений с
линейных уравнений с![]() неизвестными:
неизвестными:
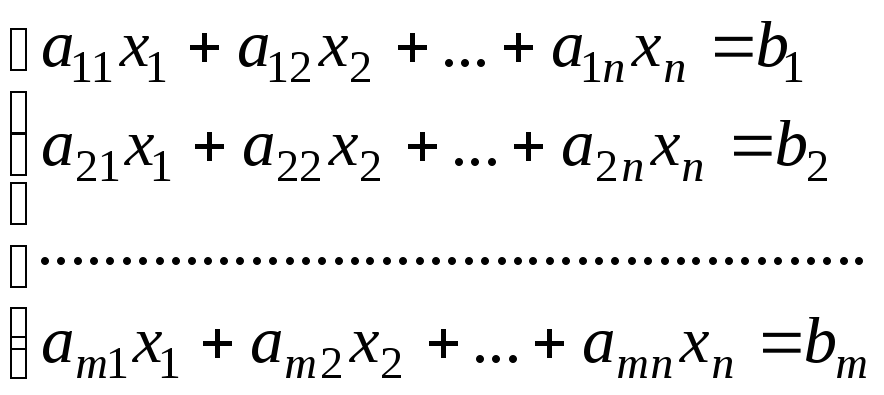 (1)
(1)
Обозначив через
![]() основную матрицу этой системы,
через
основную матрицу этой системы,
через![]() – одностолбцовую матрицу,
составленную из неизвестных этой
системы, а через
– одностолбцовую матрицу,
составленную из неизвестных этой
системы, а через![]() – одностолбцовую матрицу из ее
свободных членов, запишем систему
(1) в матричном виде:
– одностолбцовую матрицу из ее
свободных членов, запишем систему
(1) в матричном виде:
![]() .
Система линейных уравнений в
матричной записи представляет собой
частный случай матричных уравненийвида
.
Система линейных уравнений в
матричной записи представляет собой
частный случай матричных уравненийвида
![]() (2)
(2)
Уравнение вида ya=bсводятся к этому же типу матричных уравнений, поскольку(YA)T=BTи в результатеATYT=BT.
Согласно
определению умножения матриц,
![]() не имеет решений, если матрицы
не имеет решений, если матрицы![]() имеют различное число строк. Поэтому
имеет смысл рассматривать уравнение
вида (2), в которых число строк у
матриц
имеют различное число строк. Поэтому
имеет смысл рассматривать уравнение
вида (2), в которых число строк у
матриц![]() и
и![]() одно и то же.
одно и то же.
В равенстве
![]() первый столбец матрицы
первый столбец матрицы![]() является произведением матрицы
является произведением матрицы![]() на первый столбец матрицы
на первый столбец матрицы![]() ,
второй столбец – произведением
матрицыАна второй столбец
матрицы
,
второй столбец – произведением
матрицыАна второй столбец
матрицы![]() и т.д. Если
и т.д. Если![]() столбцовая матрица, то матричное
уравнение
столбцовая матрица, то матричное
уравнение![]() распадается на систему
распадается на систему![]() матричных уравнений:
матричных уравнений:![]() Каждое из этих матричных уравнений
является системой линейных уравнений,
причем все они имеют матрицу
Каждое из этих матричных уравнений
является системой линейных уравнений,
причем все они имеют матрицу![]() своей основной матрицей, и их
решениями будут столбцы неизвестной
матрицы
своей основной матрицей, и их
решениями будут столбцы неизвестной
матрицы![]() .
Обычно, все эти линейные системы
решаются одновременно, в виде пакета.
Приведенные рассуждения позволяют,
применив критерий Кроникера-Капелли,
установить критерий разрешимости
матричных уравнений: матичное
уравнение
.
Обычно, все эти линейные системы
решаются одновременно, в виде пакета.
Приведенные рассуждения позволяют,
применив критерий Кроникера-Капелли,
установить критерий разрешимости
матричных уравнений: матичное
уравнение
![]() имеет решение тогда и только тогда,
когда ранг матрицы
имеет решение тогда и только тогда,
когда ранг матрицы![]() равен рангу матрицы (АВ),
т. e. матрицы
полученной из матрицы
равен рангу матрицы (АВ),
т. e. матрицы
полученной из матрицы
![]() присоединением к ней матрицы
присоединением к ней матрицы![]() .
.
Квадратную матрицу, ранг которой равен ее порядку, называют невырожденной. Если ранг квадратной матрицы меньше ее порядка, матрицу называютвырожденной.
Заметим, что
если в матричном уравнении
![]() матрица
матрица![]() невырожденная, то это уравнение
имеет единственное решение, так
как каждая из систем линейных
уравнений, на которые оно распадается,
будет совместной и определенной.
невырожденная, то это уравнение
имеет единственное решение, так
как каждая из систем линейных
уравнений, на которые оно распадается,
будет совместной и определенной.
Квадратную
![]() – матрицу вида:
– матрицу вида: называют единичнойи обозначают
называют единичнойи обозначают![]() либо
либо![]() ,
если размеры известны или
подразумеваются. Очевидно, что если
,
если размеры известны или
подразумеваются. Очевидно, что если![]() – квадратная
– квадратная![]() матрица, то
матрица, то![]() .
.
Если
![]() ,
то матрицу
,
то матрицу![]() называютправой обратной для
матрицы
называютправой обратной для
матрицы![]() а матрицуA–левой
обратнойдля матрицыC.
а матрицуA–левой
обратнойдля матрицыC.
Видно, что
матрица Cявляется
решением матричного уравнения![]() ,
причем, еслиA –
невырожденная матрица, это решение
единственное. Следовательно,всякая невырожденная матрица имеет
единственную правую обратную
матрицу. Обозначим правую обратную
матрицу для матрицыAчерез
,
причем, еслиA –
невырожденная матрица, это решение
единственное. Следовательно,всякая невырожденная матрица имеет
единственную правую обратную
матрицу. Обозначим правую обратную
матрицу для матрицыAчерез![]() .
.
Ранг матрицы
![]() равен ее порядку, а если произведение
матриц – матрица невырожденная, то
согласно первой теореме о ранге
произведения матриц, невырожденным
будет и каждый сомножитель. Поэтому,
если
равен ее порядку, а если произведение
матриц – матрица невырожденная, то
согласно первой теореме о ранге
произведения матриц, невырожденным
будет и каждый сомножитель. Поэтому,
если![]()
![]() то
то![]() – тоже невырожденная и имеет для
себя правую обратную. Пусть это
будет матрицаD,
т.e.
– тоже невырожденная и имеет для
себя правую обратную. Пусть это
будет матрицаD,
т.e.![]() .
Тогда с одной стороны
.
Тогда с одной стороны![]() с другой –
с другой –![]() откуда вследствии ассоциативности
умножения матриц
откуда вследствии ассоциативности
умножения матриц![]() и
и![]() т.e. правая обратная
матрица
т.e. правая обратная
матрица![]() будет и ее левой обратной. Итак,всякая невырожденная матрица
будет и ее левой обратной. Итак,всякая невырожденная матрица
![]() имеет единственную обратную
двустороннюю матрицу,которую
обозначают
имеет единственную обратную
двустороннюю матрицу,которую
обозначают![]() :
:
![]() .
.
Одним из способов
нахождения матрицы, обратной для
матрицы
![]() ,
является решение матричного
уравнения
,
является решение матричного
уравнения![]() .
.
Согласно первой
теореме о ранге произведения матриц,
![]() .
Если матрицаАневырожденная, то
матрицуВможно записать в виде
В=А–1(АВ), и
тогда (по той же теореме)
.
Если матрицаАневырожденная, то
матрицуВможно записать в виде
В=А–1(АВ), и
тогда (по той же теореме)![]() .
Тем самым доказанавторая теорема
о ранге произведения матриц:если
матрицаA
невырожденная, то
.
Тем самым доказанавторая теорема
о ранге произведения матриц:если
матрицаA
невырожденная, то![]()
Задача
1. Вычислить![]() где
где![]()
Решение. Так как в данное выражение вместо переменных подставляются матрицы, можно считать, что число 4 умножено на единичную матрицу, т. е. 4 надо понимать как 4Е:
![]() .
.
Ответ:
![]() .
.
Задача 2. ВычислитьAB, где
A=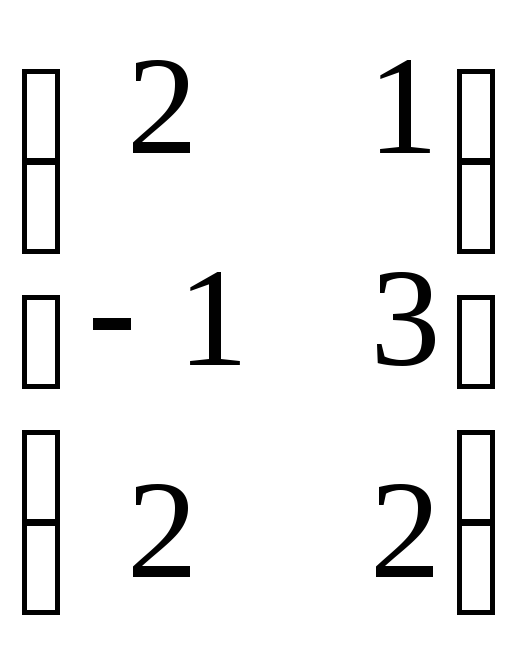 ,B=
,B=![]() .
.
Решение. Число столбцов матрицыАравно числу строк матрицыB, значит произведениеАВсуществует (ноВАв этом случае не существует).
По определению
произведения матриц для вычисления
элемента cijматрицыС=АВ( т. е. элемента в
i-й строке и j-м столбце), следует i-ю
строку матрицыАумножить на j-й
столбец матрицыВ(![]() ).
Например,
).
Например,
![]() =
=![]() .
Запишем:C=
.
Запишем:C=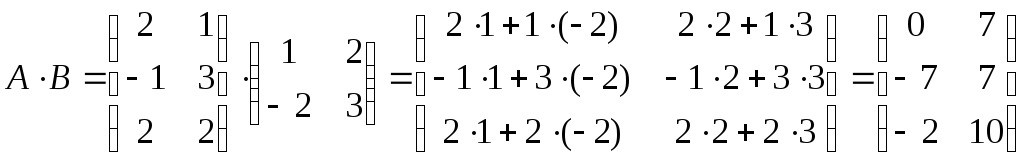 .
.
Ответ: C=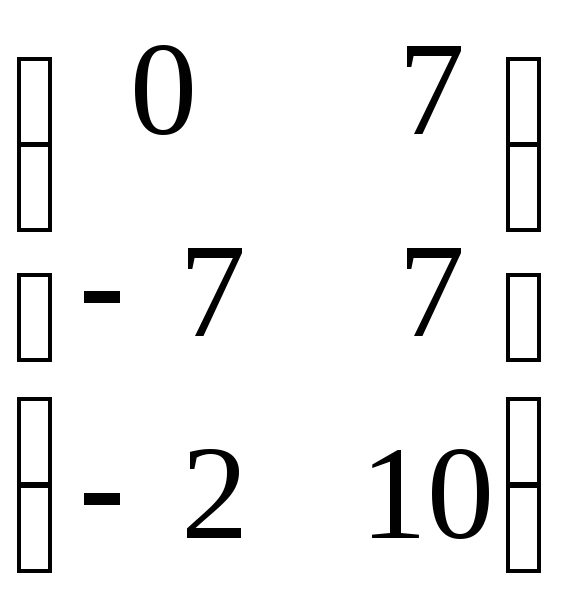 .
.
Задача 3. ВычислитьАВиВА, если они существуют:
a)A=![]() ,B=
,B=![]() б)А=
б)А=![]() ,B=
,B=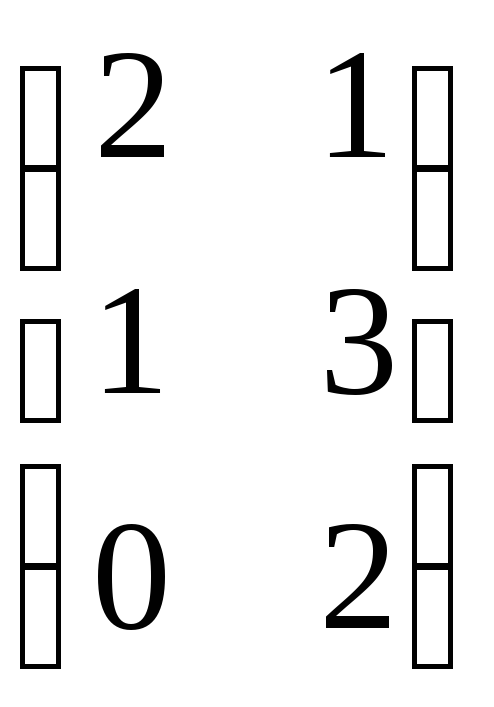 в)
А=
в)
А=![]() ,В=
,В=![]()
Решение.
а)А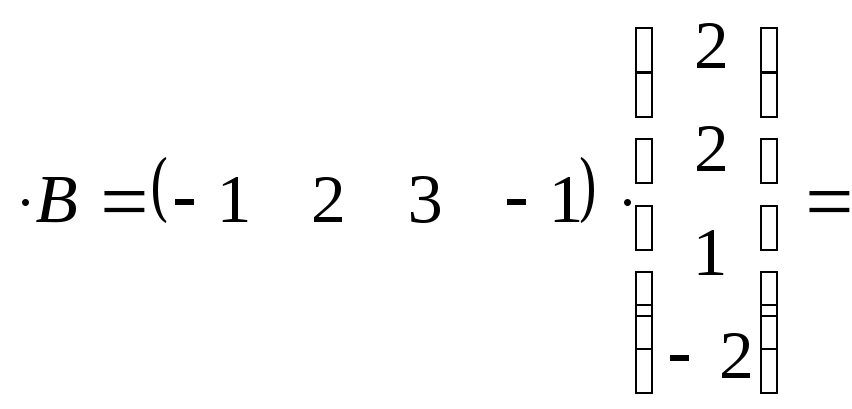 (–1
(–1![]()
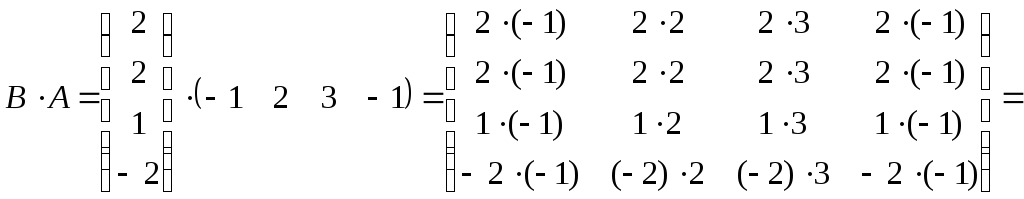 =
= .
б)
.
б)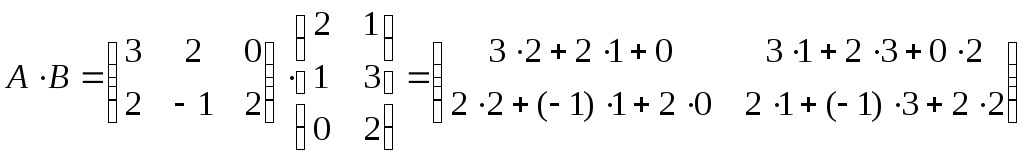 =
=![]() .
.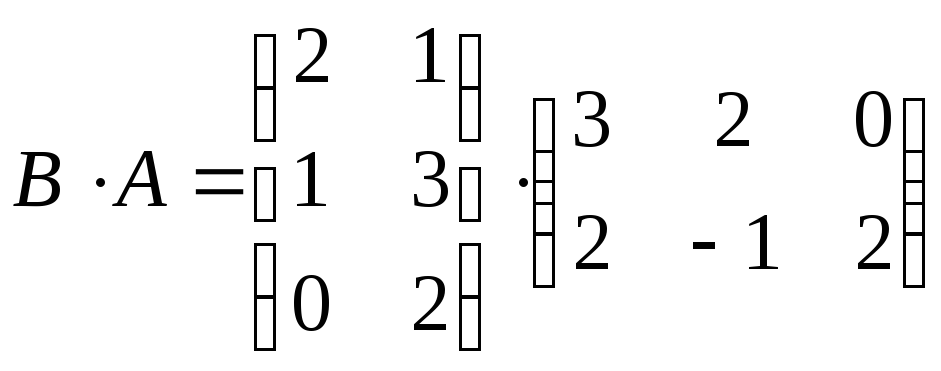 =
=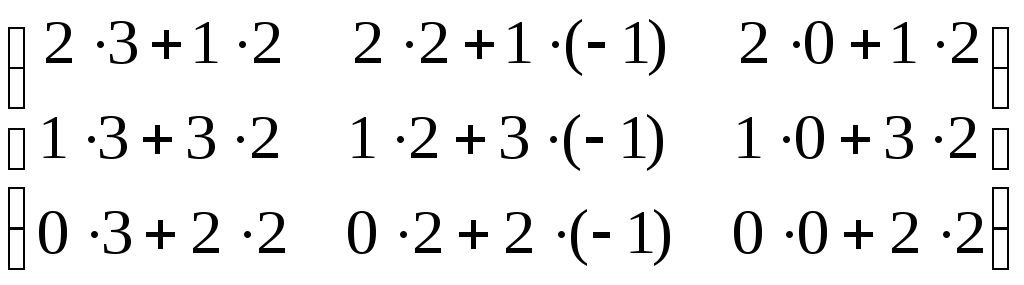 =
=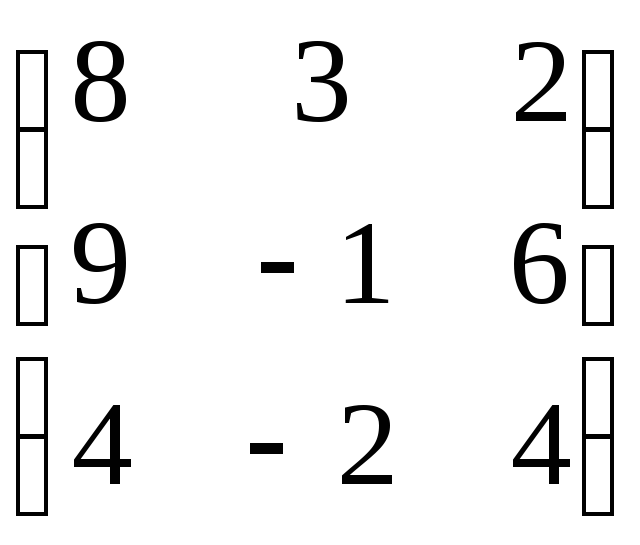 .
в)
.
в)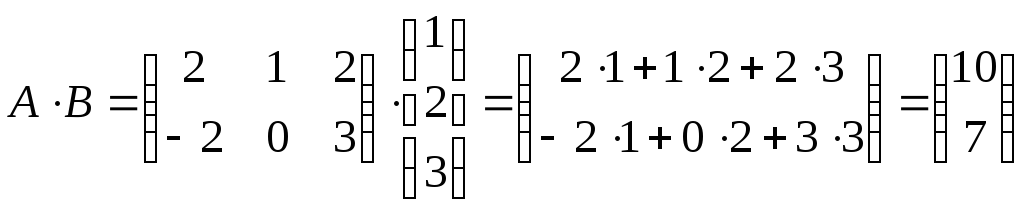 ,
,![]() не существует.
не существует.
Ответ: a)
![]() ,
,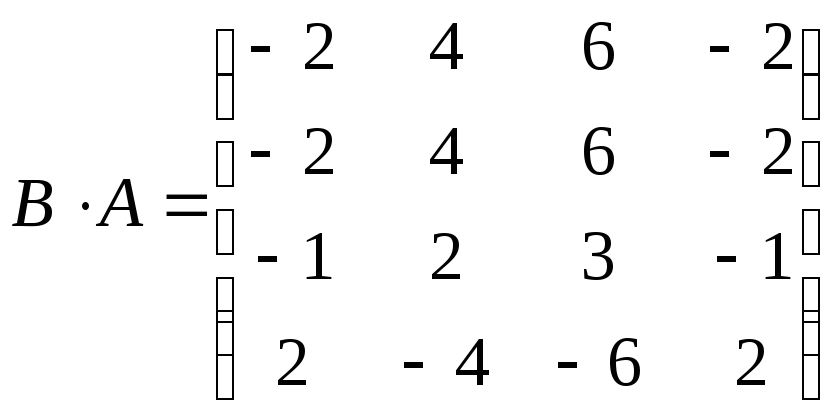 ;б)
;б)
![]() ,
,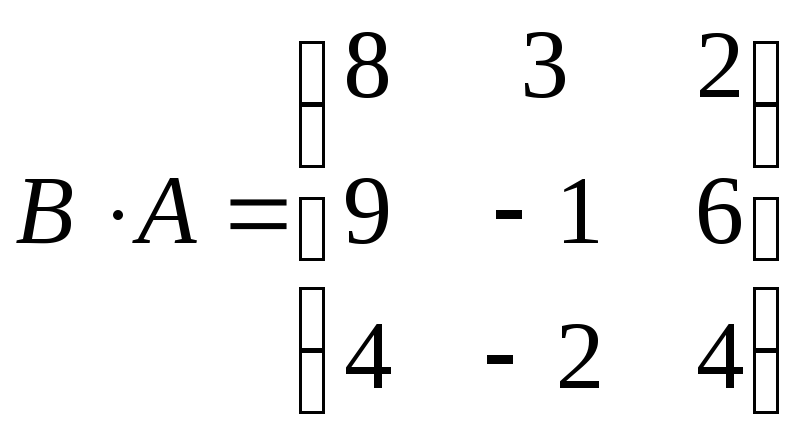 ;в)
;в)
![]() ,
,![]() не существует.
не существует.
Задача 4. Вычислить f(A), если f(x)=x2–2x+1,
A=![]()
Решение.
f(A)=![]() =
=
=
=![]() =
=
=
=![]()
Ответ:
f(A)=![]() .
.
Задача 5. Решить матричное уравнение видаАХ=В.
а)
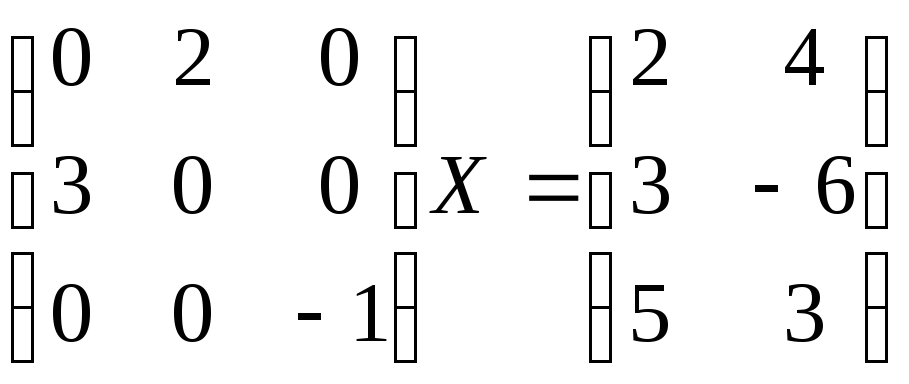 б)
б)![]()
в)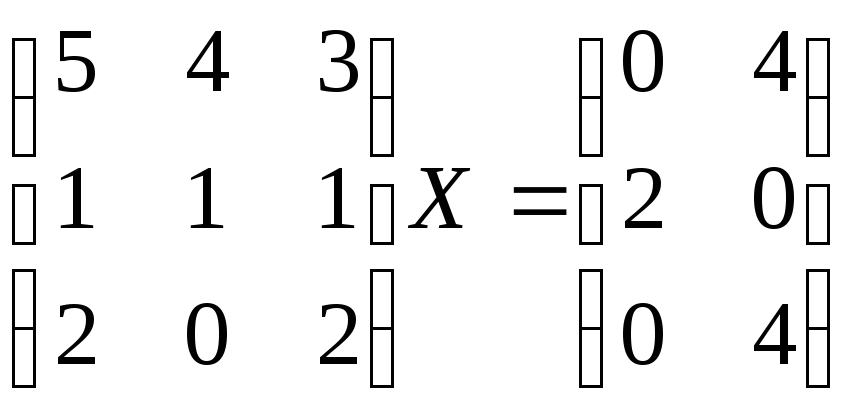 г)
г)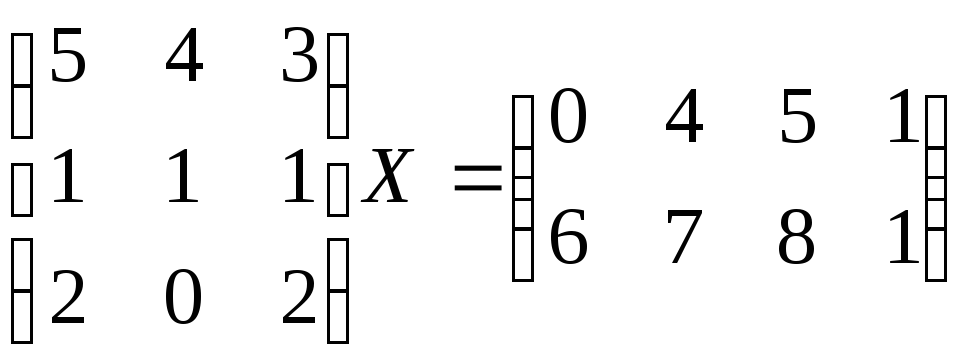
Решение. МатрицаХдолжна иметь столько строк, сколько столбцов у матрицыА, и столько столбцов, сколько столбцов у матрицыВ. Для существования решения уравненияАХ=Внеобходимо, чтобы матрицыАиВимели одинаковое число строк. Поэтому в случае г) уравнение решения не имеет.
а) Матрица А –
размера![]() ,
матрицаВ – размера
,
матрицаВ – размера![]() .
Поэтому матрицаХразмера –
.
Поэтому матрицаХразмера –![]() ,
,
Х=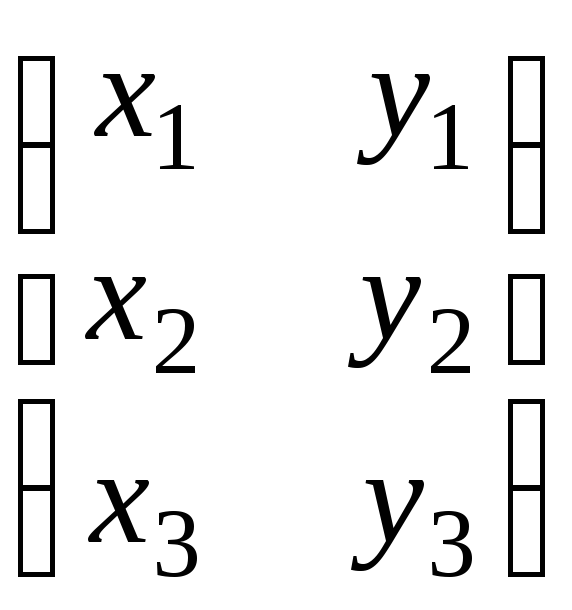 ТогдаАХ=Вможно записать так:
ТогдаАХ=Вможно записать так: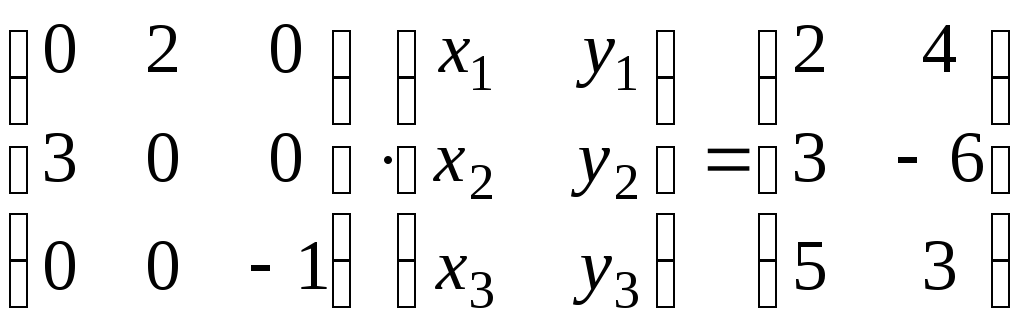 ;
;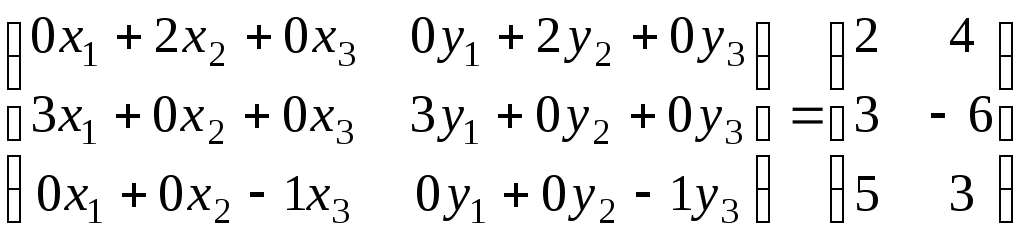 ;
;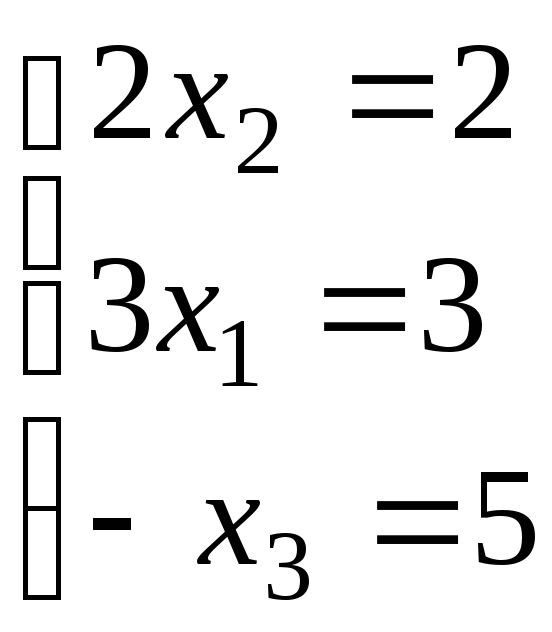 и
и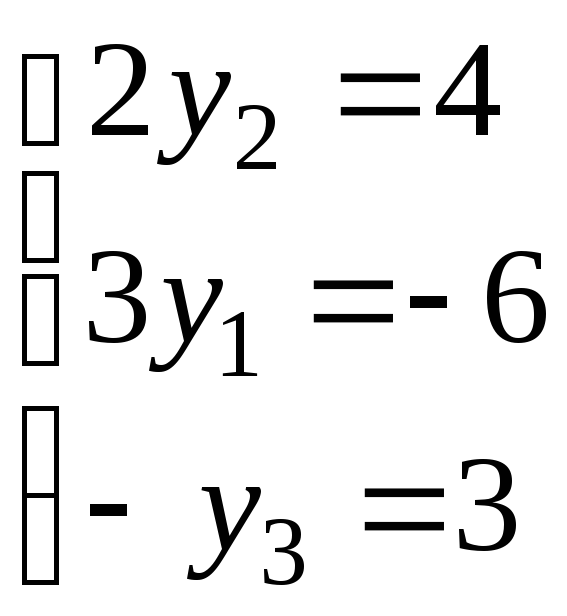 .откуда
.откуда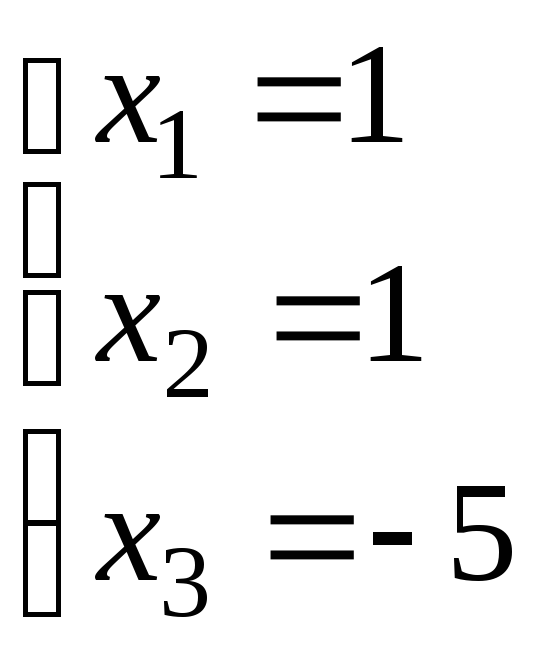 и
и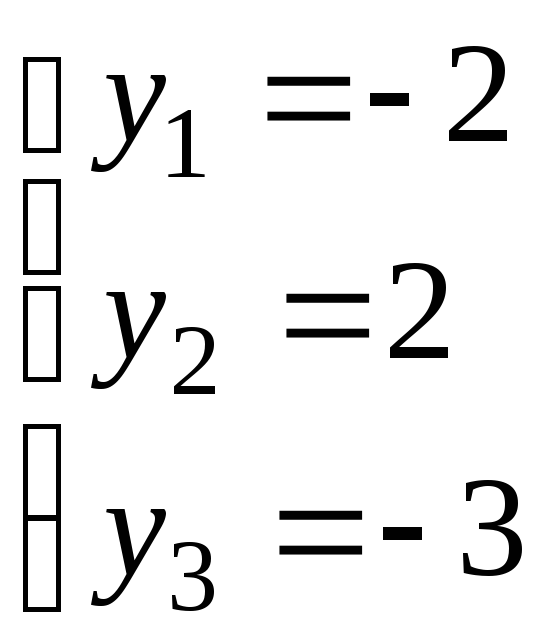 .
ИтакX=
.
ИтакX=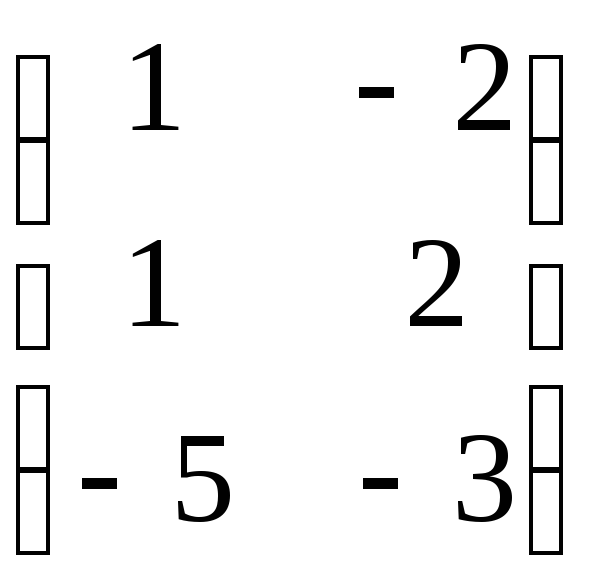 .
.
Проверка:
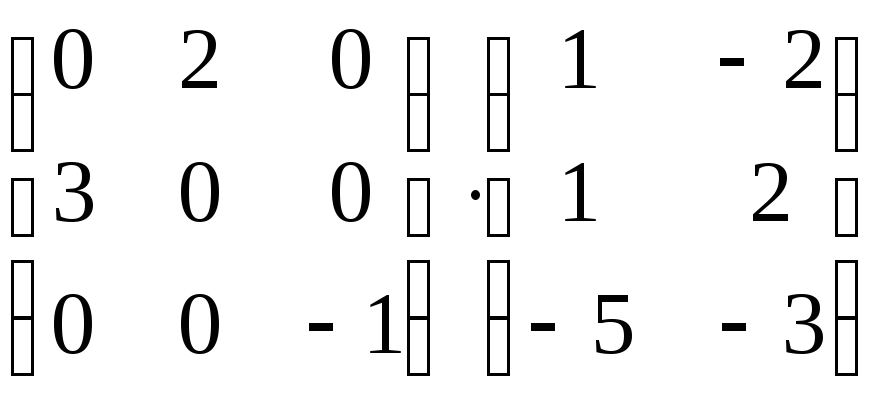 =
=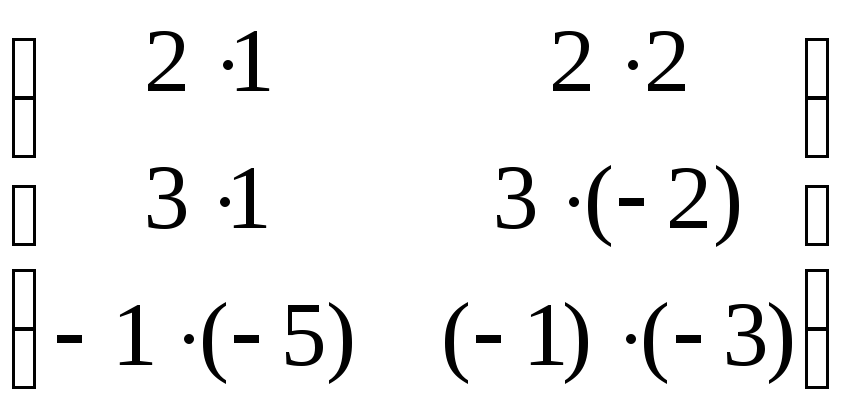 =
=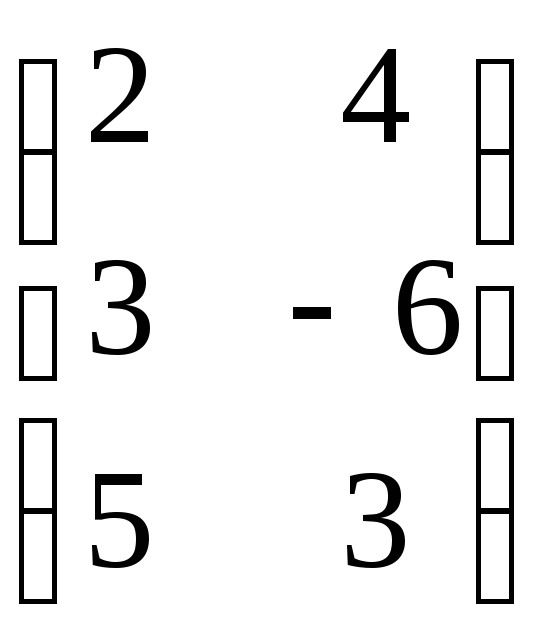 .
.
2 способ.Матричное равенствоАС=Вне
измениться при одинаковых элементарных
преобразованиях систем строк матрицАиВ. Поэтому, при одинаковых
элементарных преобразованиях систем
строк матрицАиВуравнениеАХ=Впереходит в равносильное.
Поменяем местами первую и вторую
строки, затем первую строку умножим
на (1/3), а вторую на (1/2), третью на
(–1). Получим уравнение равносильное
исходному: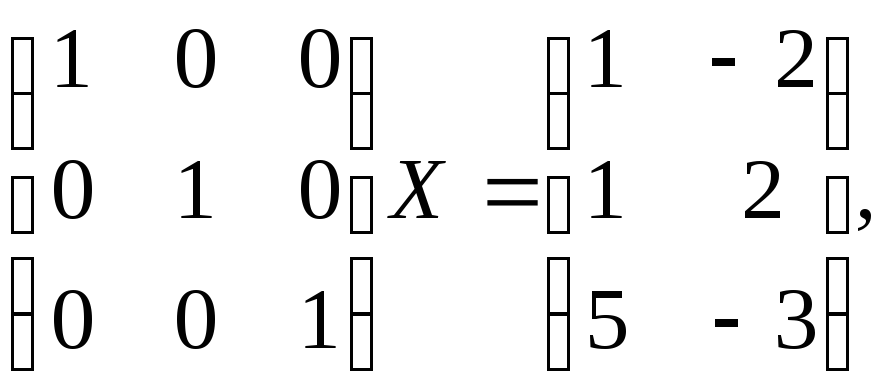 илиХ=
илиХ=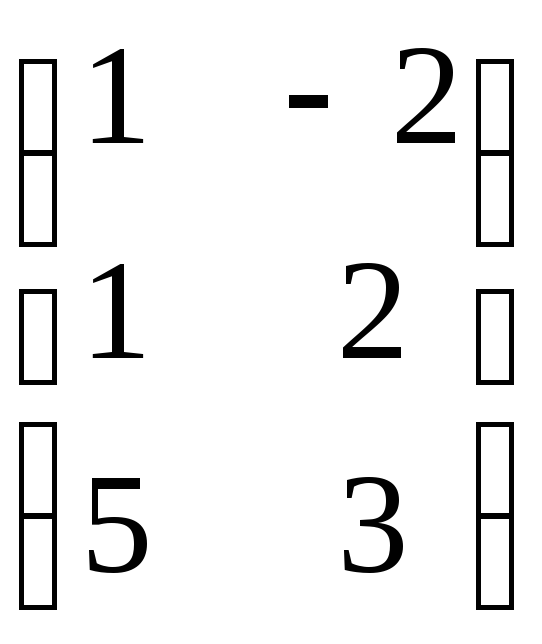 ,
т.к.Е=
,
т.к.Е=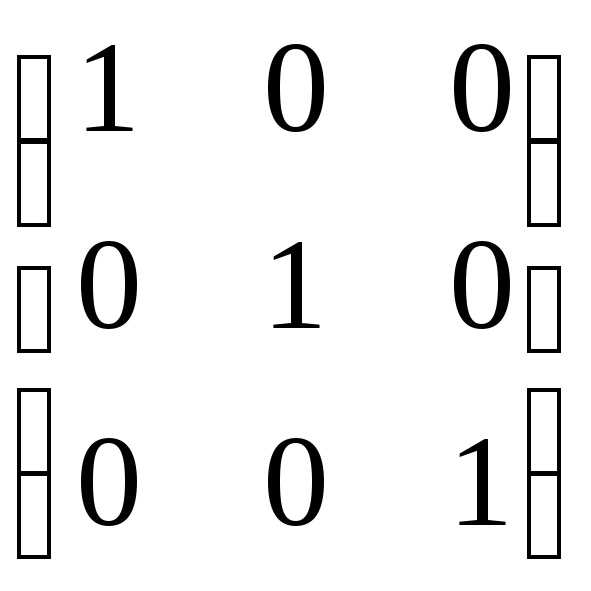 ,ЕХ=Х.
,ЕХ=Х.
б) Матрица А –
размера 3![]() 3,
матрицаВ – размера 3
3,
матрицаВ – размера 3![]() 2
. Поэтому искомая матрицаХ –
размера 3
2
. Поэтому искомая матрицаХ –
размера 3![]() 2.
Тогда исходное уравнение можно
записать в виде:
2.
Тогда исходное уравнение можно
записать в виде:
A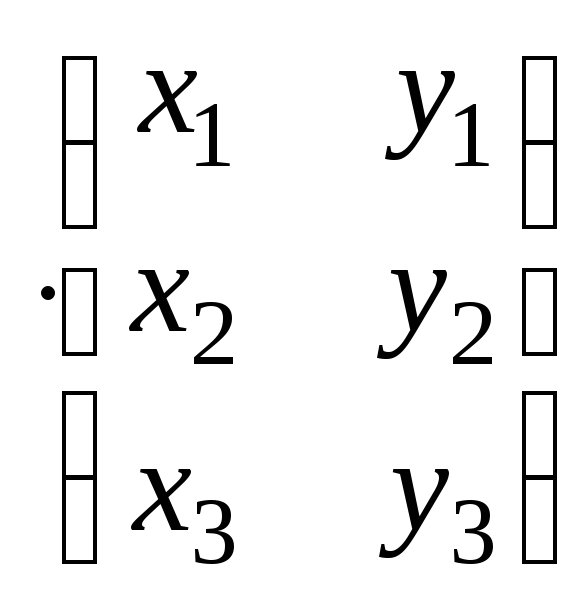 =B.
=B.
Это уравнение равносильно системе двух уравнений:
A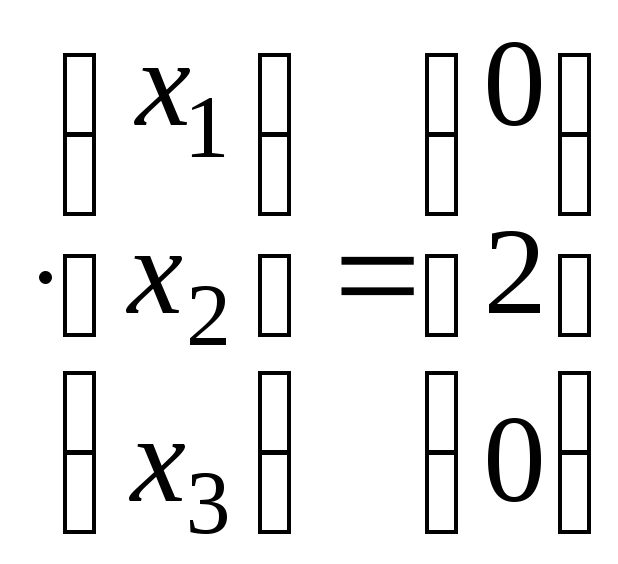 ,A
,A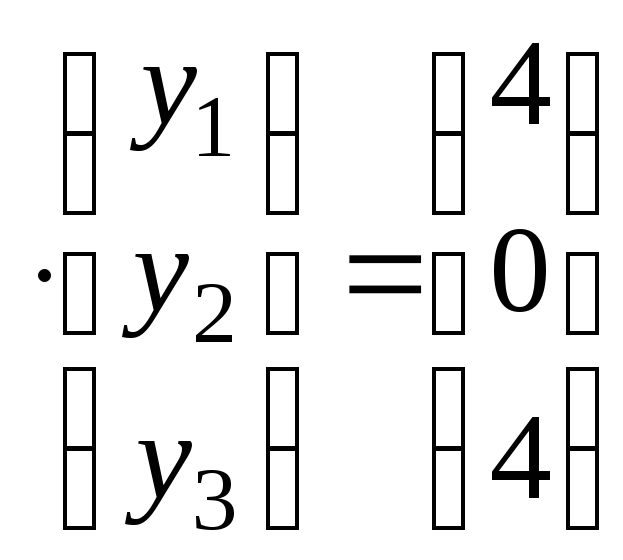 .
Каждое
из этих уравнений является системой
линейных уравнений с тремя неизвестными,
причем у обеих систем одна и та
основная матрицаА. Поэтому их
можно решать одновременно, написав
столбцы свободных членов рядом.
.
Каждое
из этих уравнений является системой
линейных уравнений с тремя неизвестными,
причем у обеих систем одна и та
основная матрицаА. Поэтому их
можно решать одновременно, написав
столбцы свободных членов рядом.
Итак, матричное
уравнение АХ=В есть пакет систем
линейных уравнений с общей основной
матрицейА: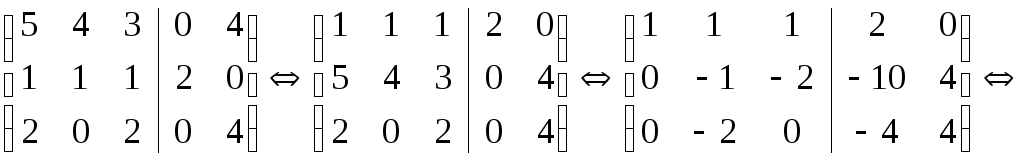
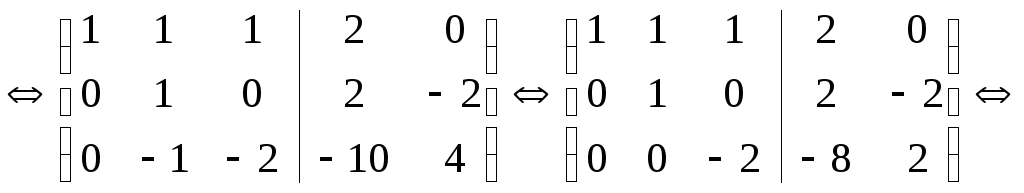
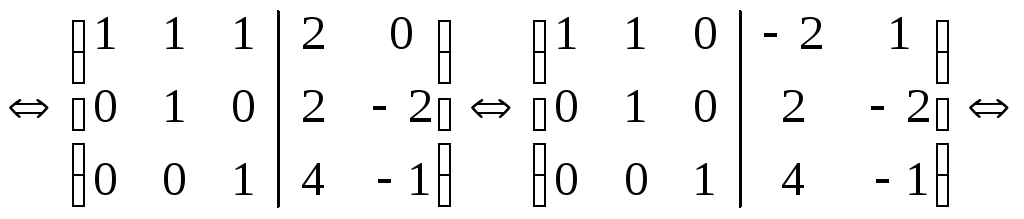
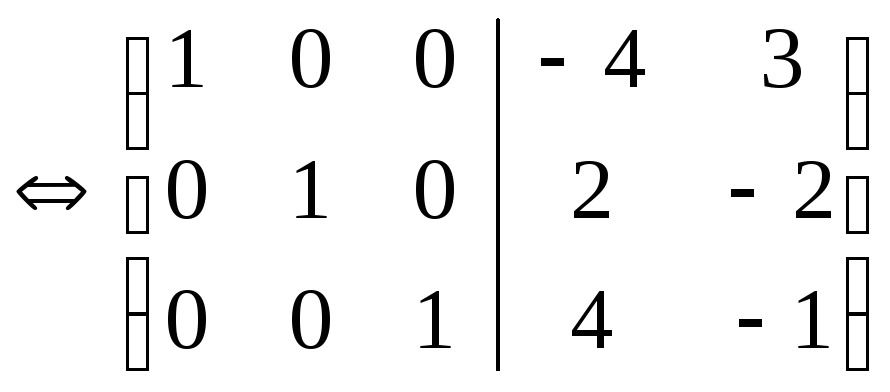 ,
т.е.Х=
,
т.е.Х=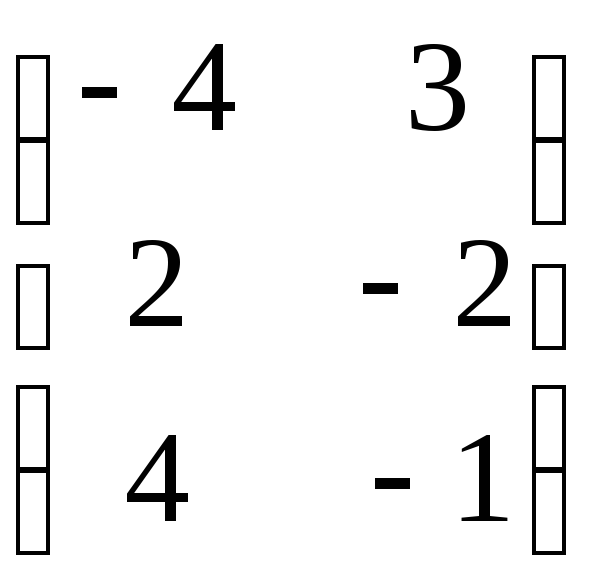 .
.
Фактически метод
решения тот же , что и в пункте а),
но элементарных преобразований
больше, т.е. одними и теми же
элементарными преобразованиями
строк матриц АиВуравнениеАХ=Вбыло преобразовано в
равносильное: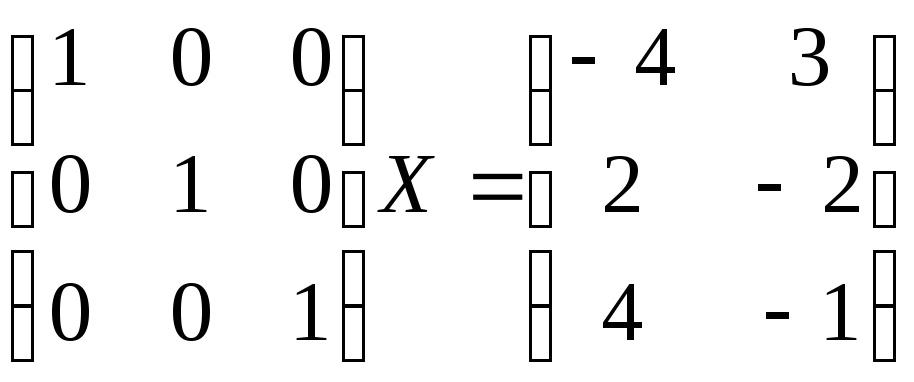 .
.
Проверка:
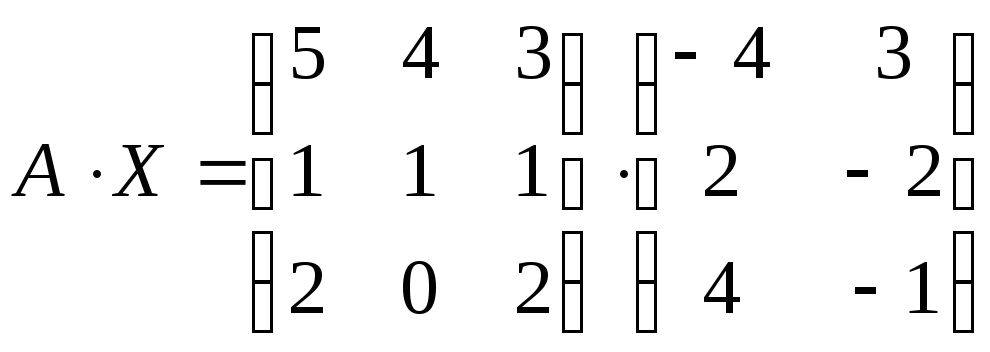 =
=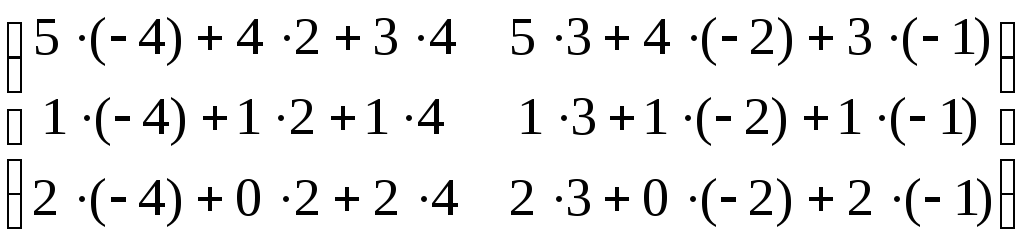 =
=
=
=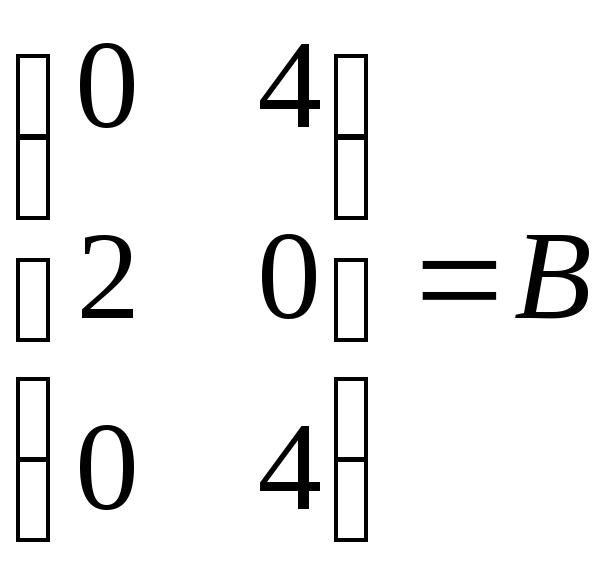 .
.
в) Решаем пакет
двух систем линейных уравнений:
![]()
![]()
![]() .
Замечаем,
что обе системы, входящие в пакет,
имеют бесконечно много решений
при одном свободном неизвестном.
Запишем их в виде:
.
Замечаем,
что обе системы, входящие в пакет,
имеют бесконечно много решений
при одном свободном неизвестном.
Запишем их в виде:
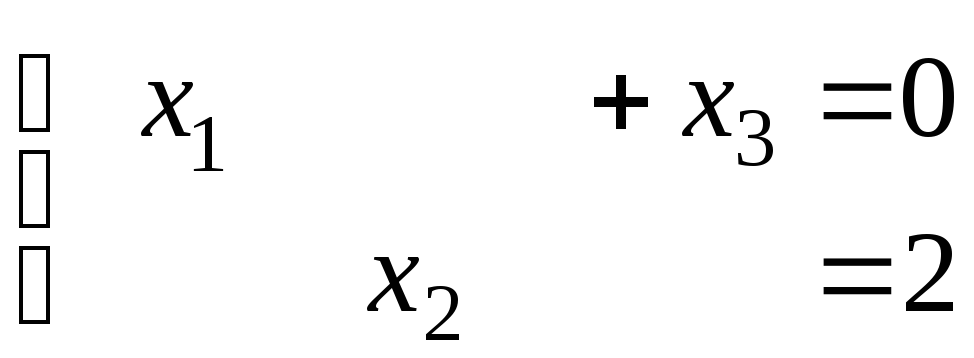 и
и 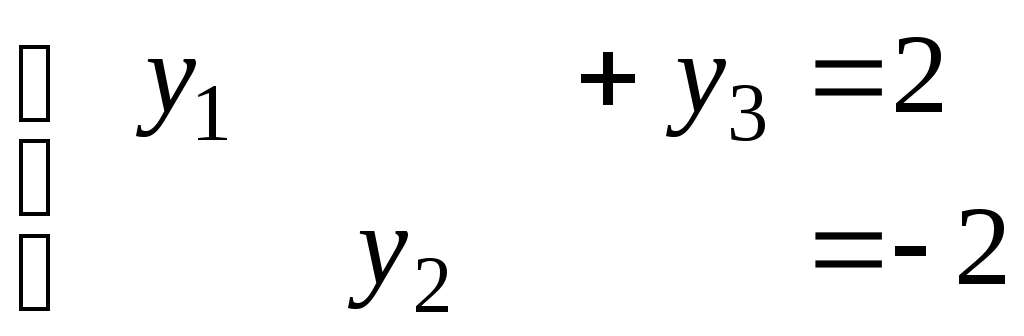 .
Значит
.
Значит
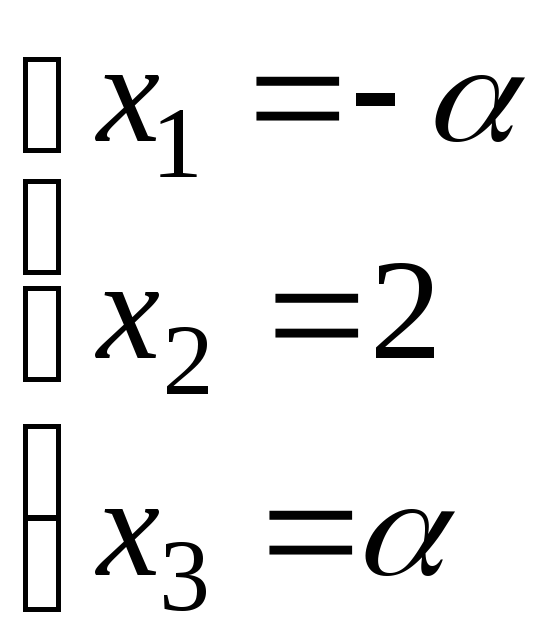 и
и 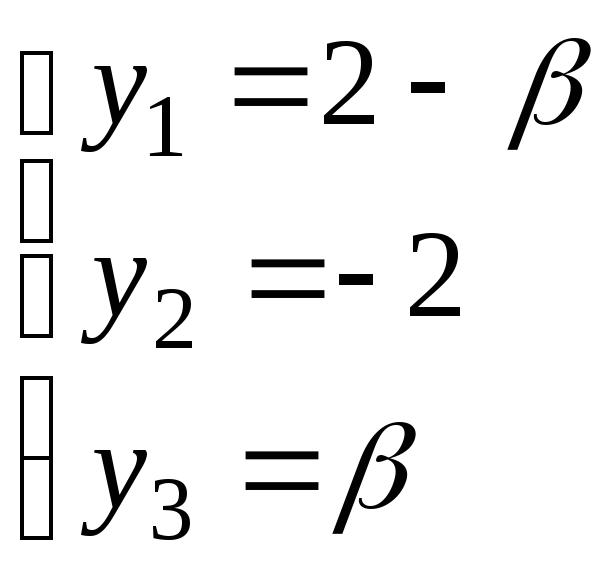 .
Поэтому
.
Поэтому
Х=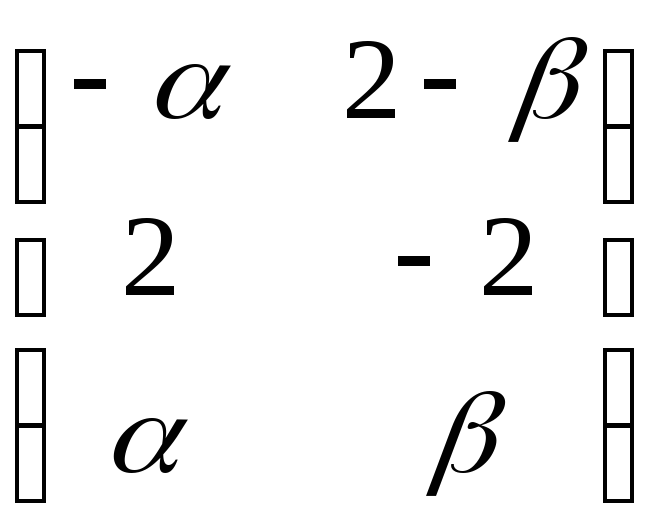 ,
где
,
где![]() –
любые числа.
–
любые числа.
Проверка:
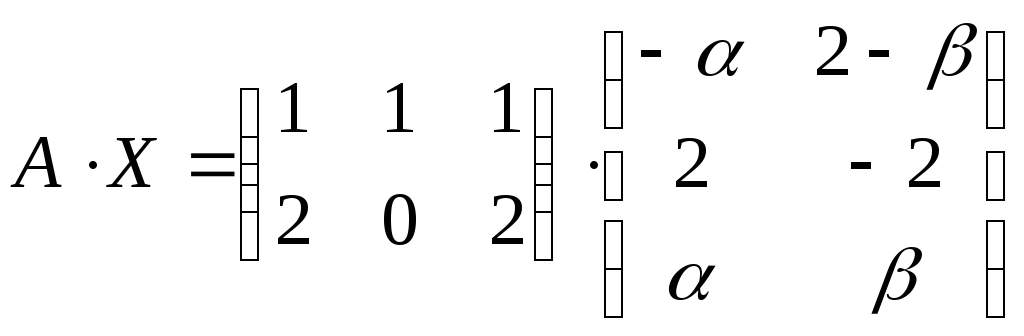 =
=
=
=![]()
Ответ:a)X=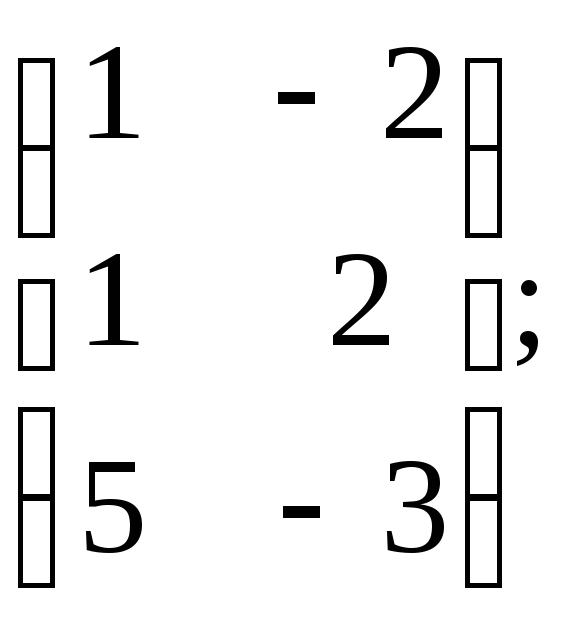 б)Х=
б)Х=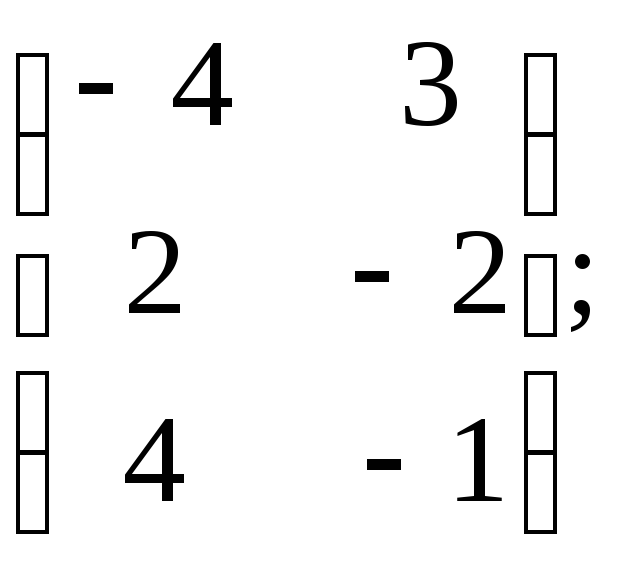
в) Х=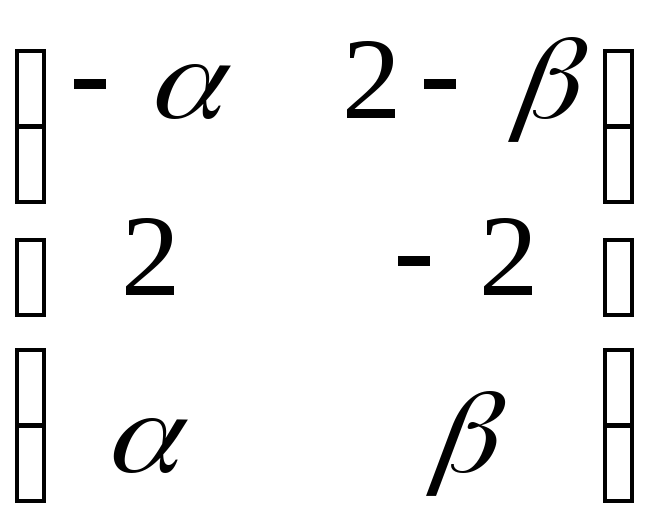 где
где![]() – любые числа; г) решений нет.
– любые числа; г) решений нет.
Задача 6.Решить матричное уравнение вида:XA=B, если:
a) A= B=
B=![]()
б)
A=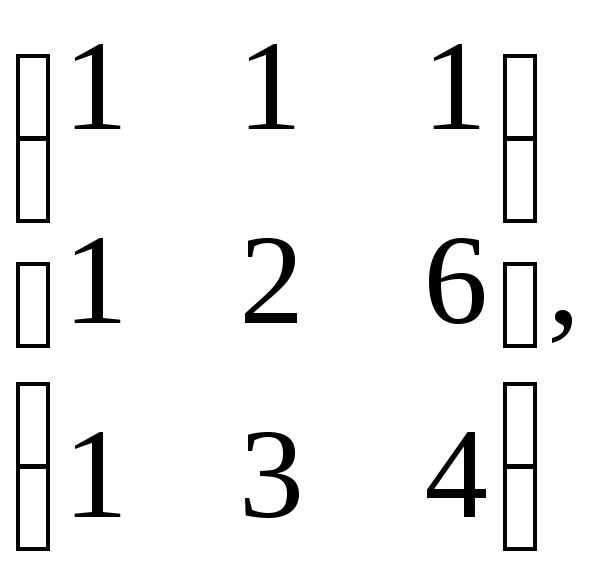 B=
B=![]()
в)
A=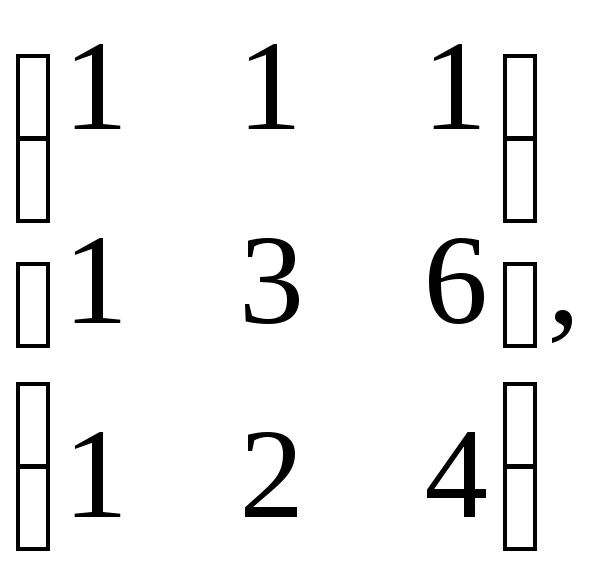 B=
B=![]()
г)
A=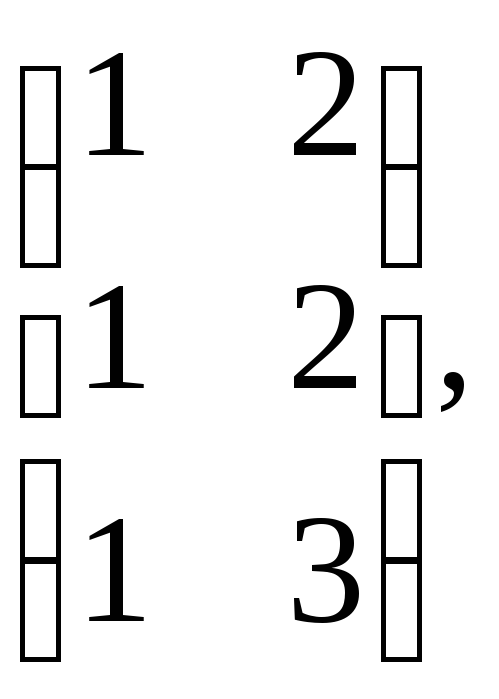 B=
B=![]()
Решение.Для существования решения необходимо равенство числа столбцов матрицА иВ. Поэтому в случае в) решения нет. На размеры матрицыХвлияет число строк матрицАиВ: число строк матрицыХ равно числу строк матрицыВ, число столбцов равно числу строк матрицыА.
а) Матрица Вразмера 2![]() 3,
матрица А размера 3
3,
матрица А размера 3![]() 3.
Поэтому матрица Х размера 2
3.
Поэтому матрица Х размера 2![]() 3,
т.е.
3,
т.е.
Х=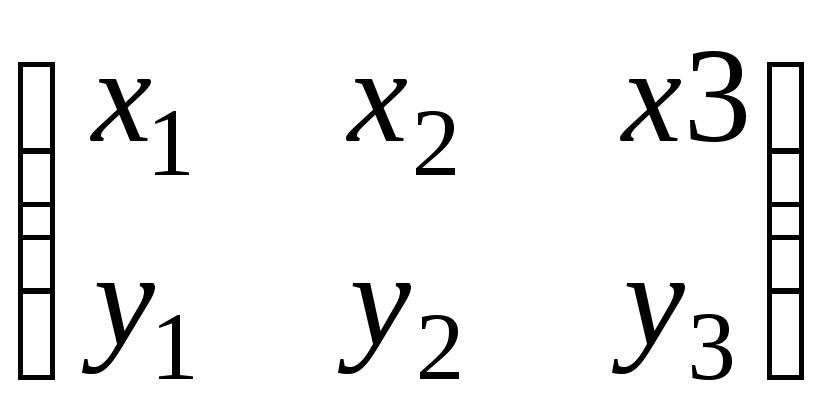 .
Тогда
уравнениеХА=Взапишется в виде:
.
Тогда
уравнениеХА=Взапишется в виде:
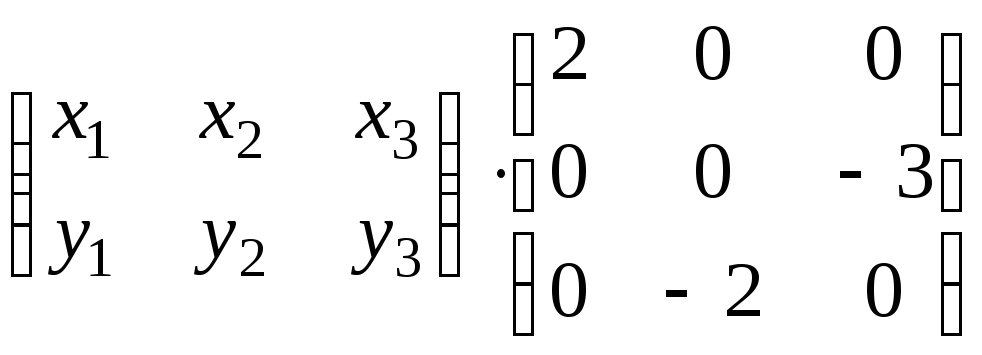 =
=![]() или
или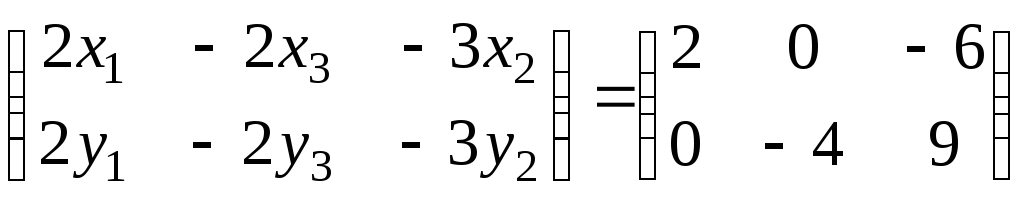 .
Откуда
.
Откуда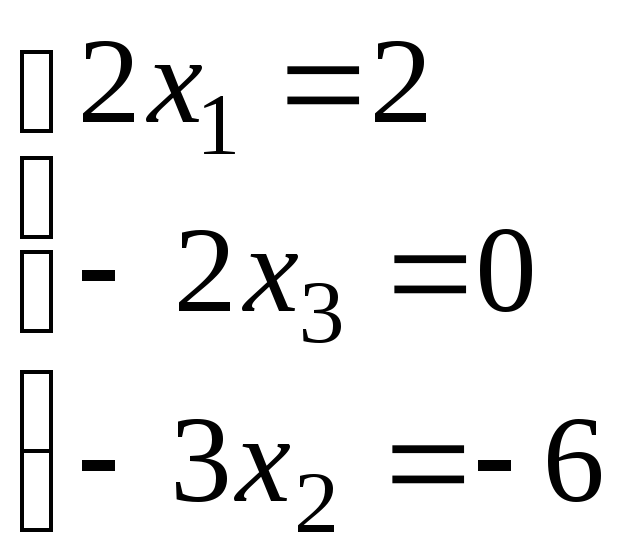 и
и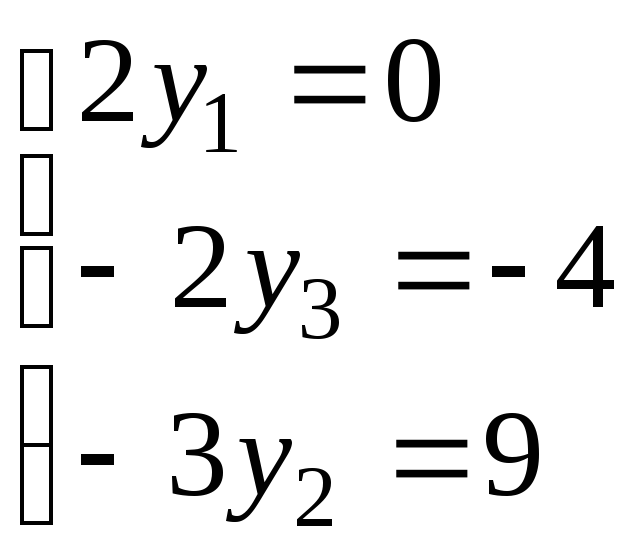 .
Поэтому
.
Поэтому и
и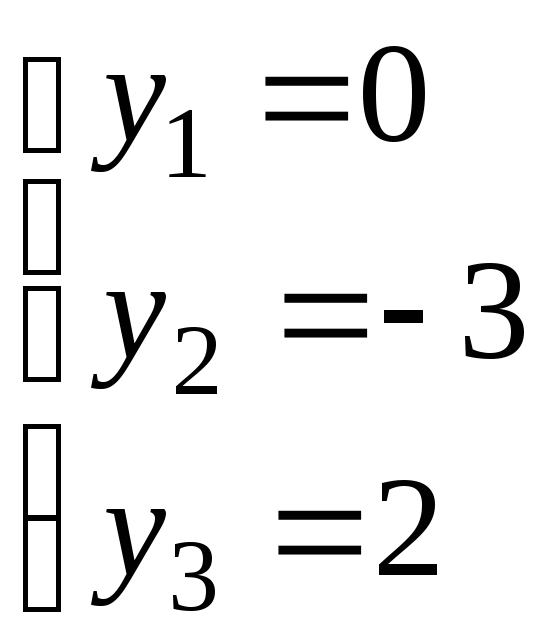 .
Тогда
.
Тогда
X=![]() .
.
Проверка:
![]()
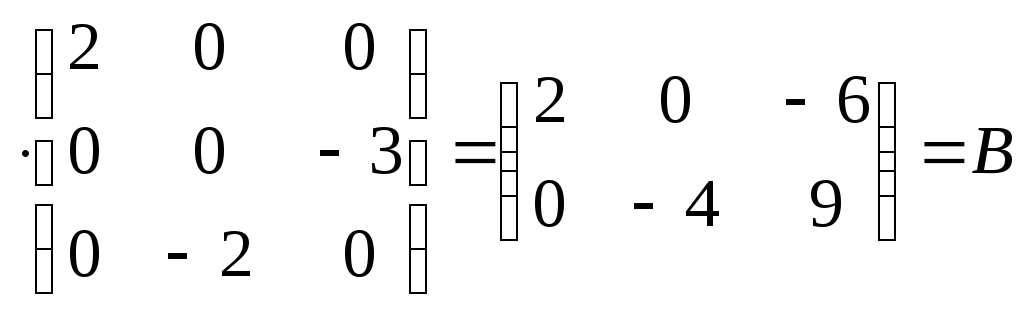 .
.
2 способ.Воспользуемся равенством![]() Тогда уравнениеХА=В перейдет в
уравнение
Тогда уравнениеХА=В перейдет в
уравнение![]() которое можно решить как пакет систем
линейных уравнений, а затем решение
транспонировать.
которое можно решить как пакет систем
линейных уравнений, а затем решение
транспонировать.
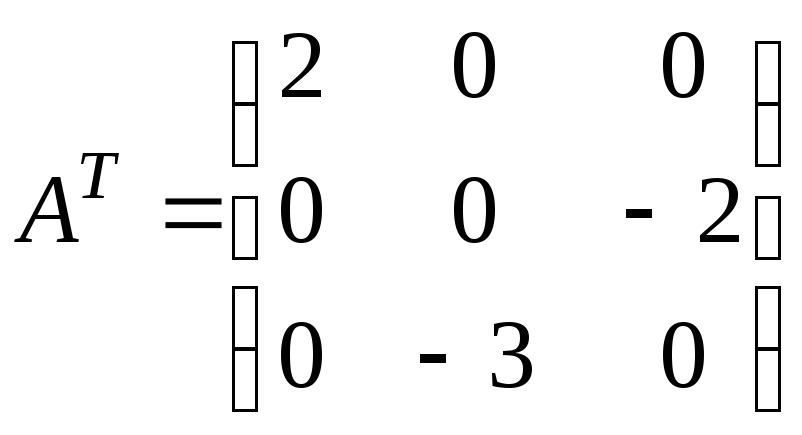
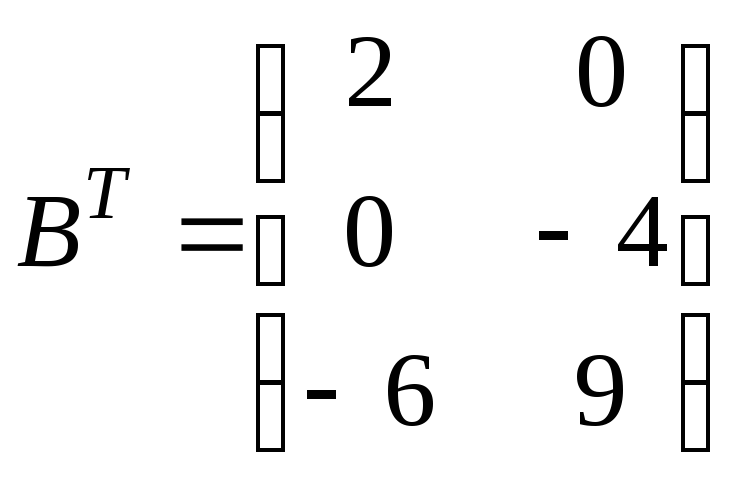
Решаем пакет
двух систем уравнений:
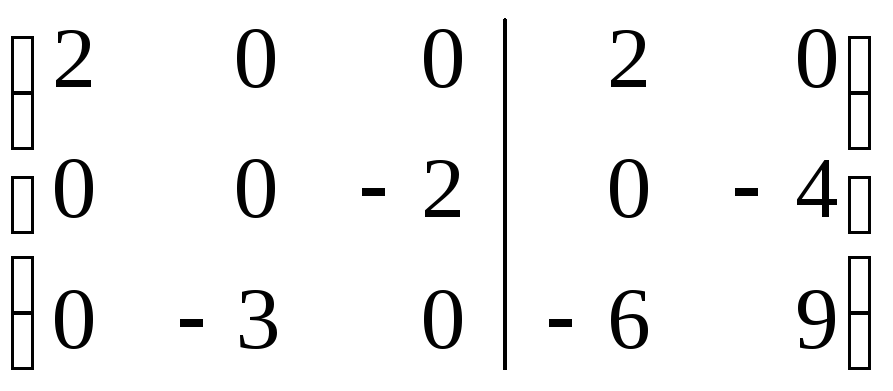
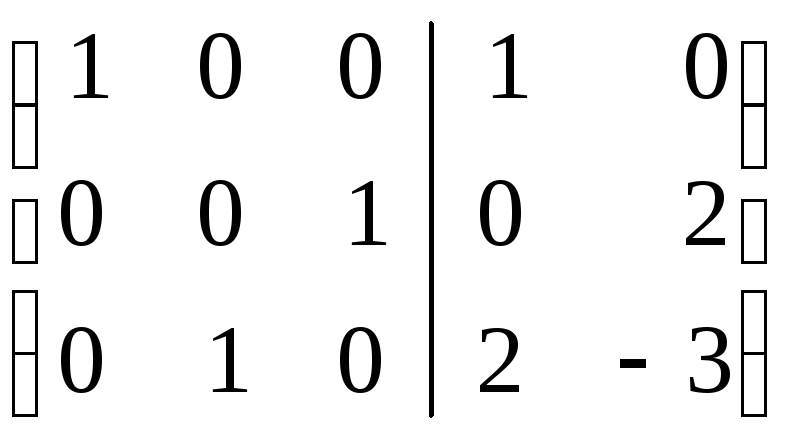
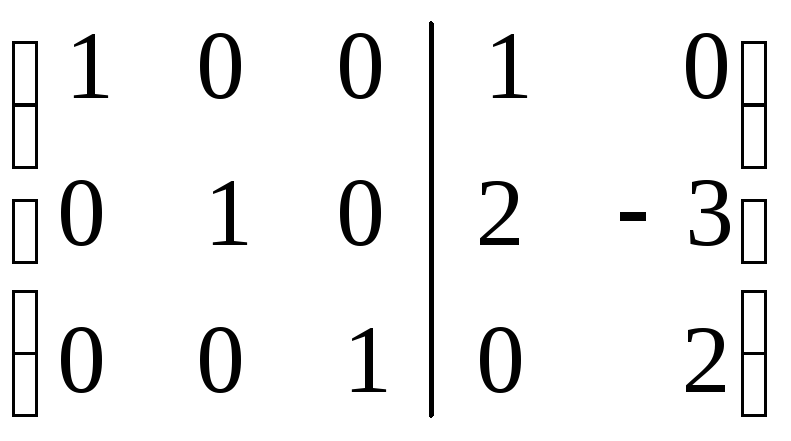 Тогда
Тогда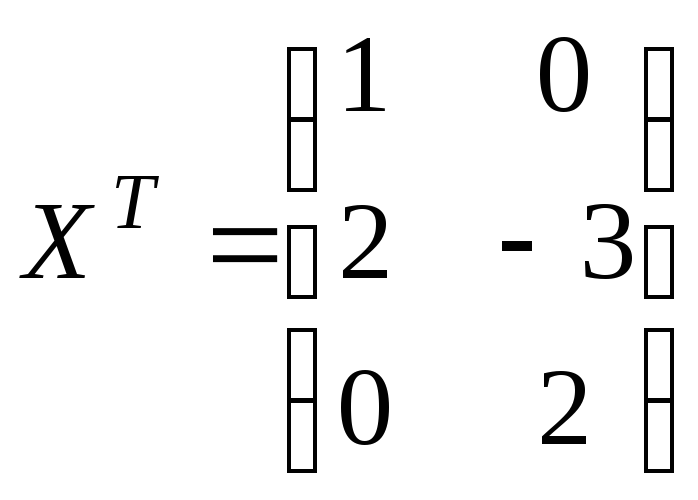 или
или![]() .
.
б)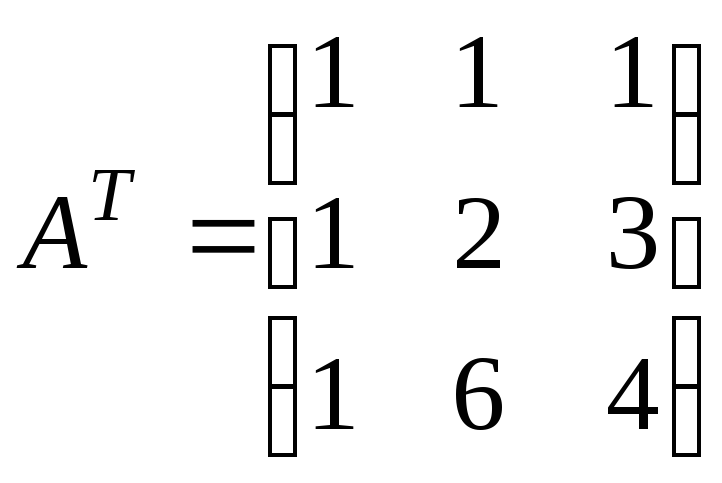 ,
,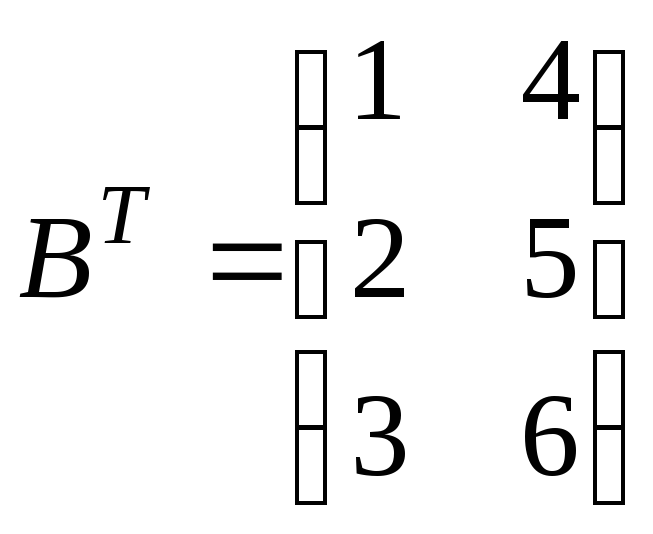 .
Решаем
пакет систем уравнений:
.
Решаем
пакет систем уравнений: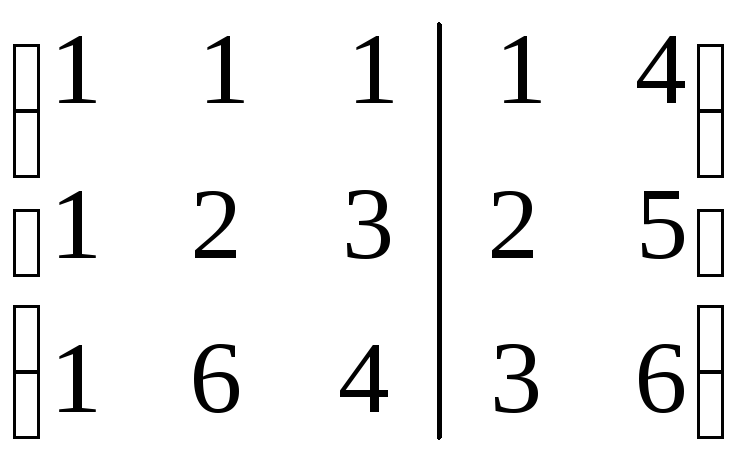
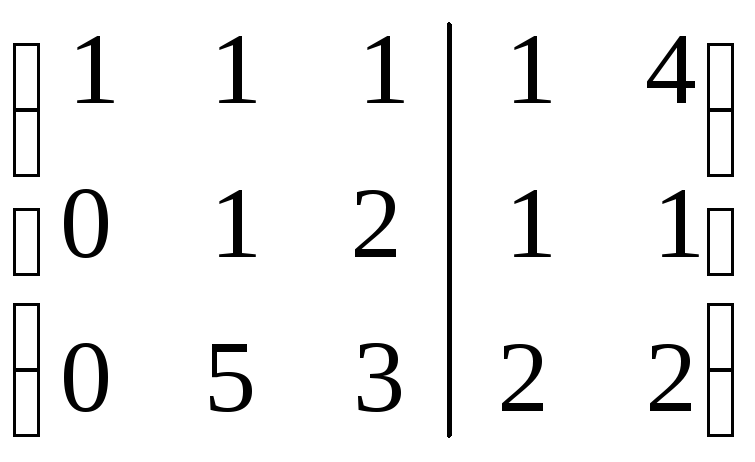
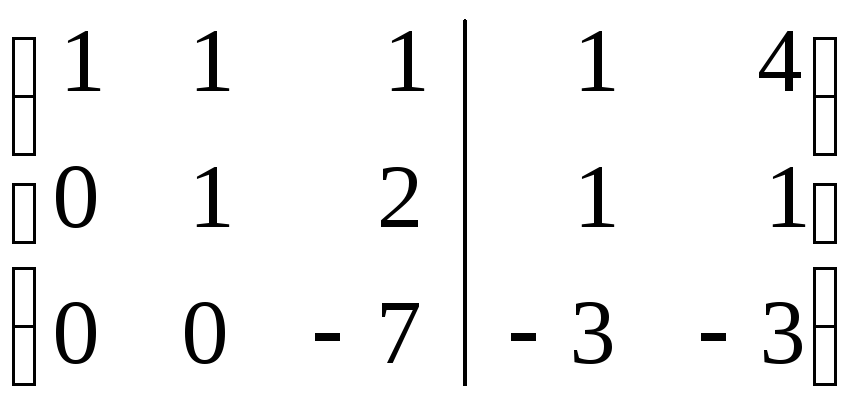

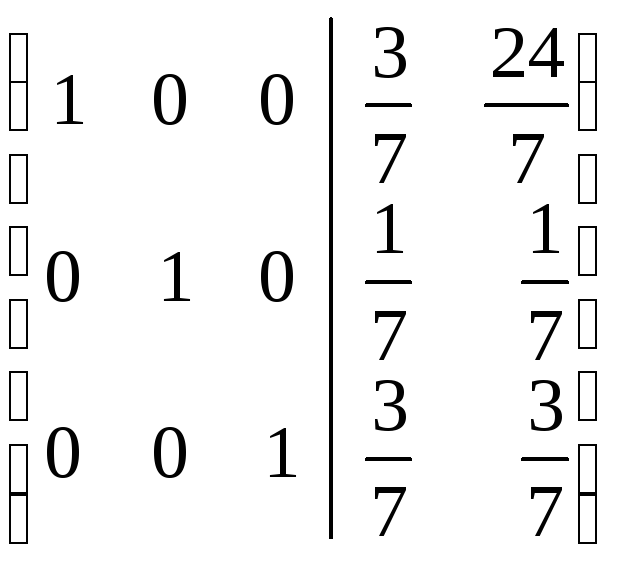 .
Тогда
.
Тогда или
или![]() .
.
Проверка:![]() XA=
XA=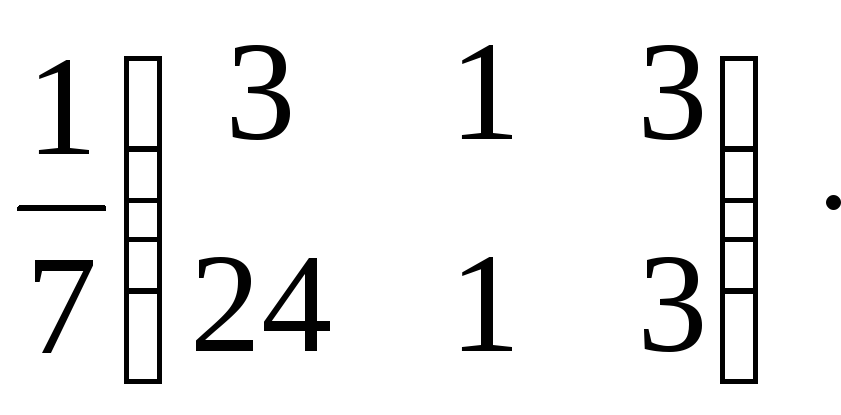
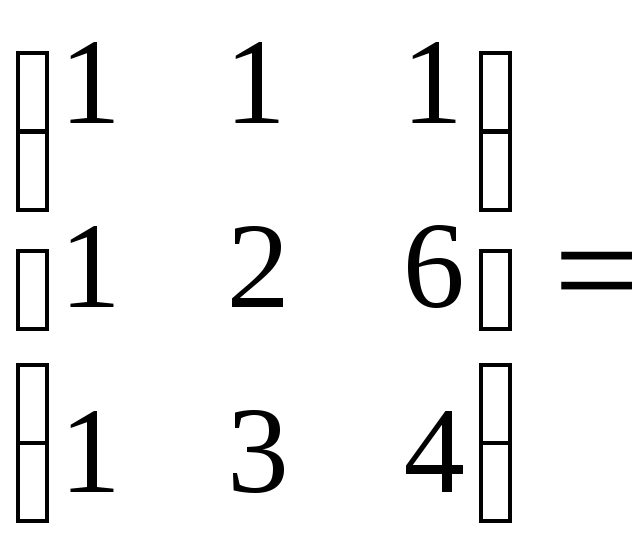
![]() г)AT=
г)AT=![]() ,B=
,B=![]() .
Решаем
пакет двух систем уравнений:
.
Решаем
пакет двух систем уравнений:
![]()
![]()
![]() Откуда
Откуда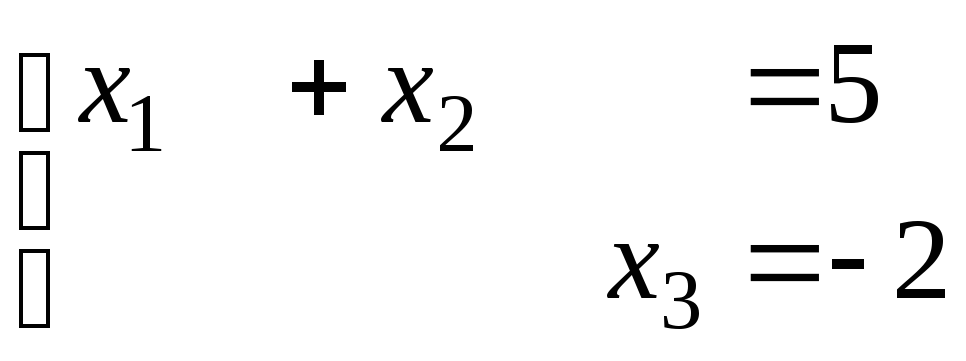 и
и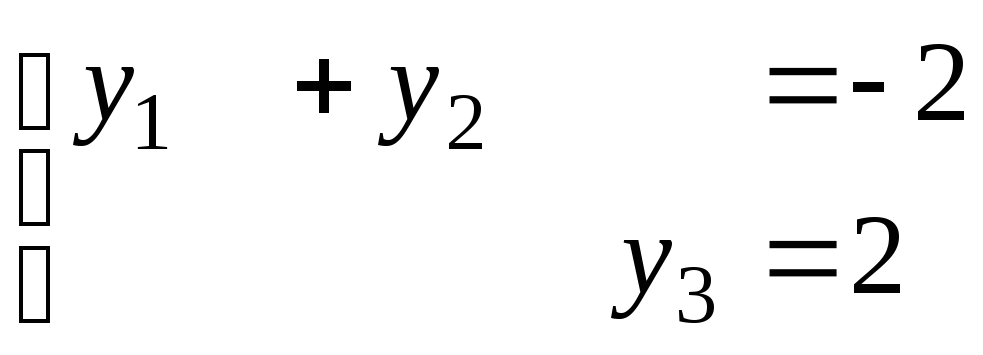 .
Системы
являются совместными неопределёнными
и имеют решения:
.
Системы
являются совместными неопределёнными
и имеют решения: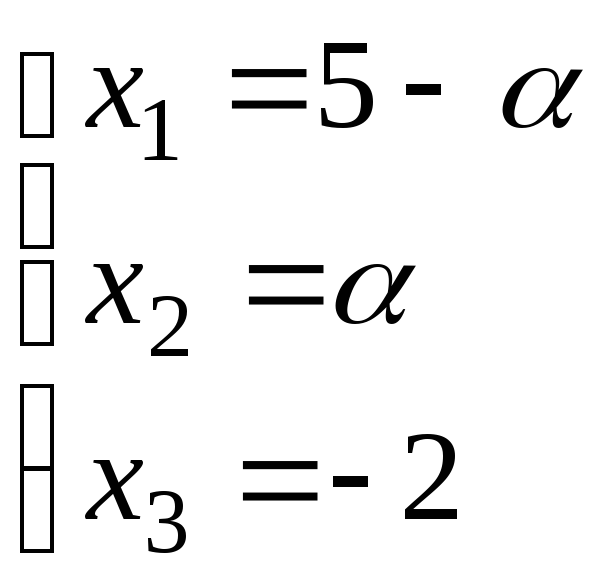 и
и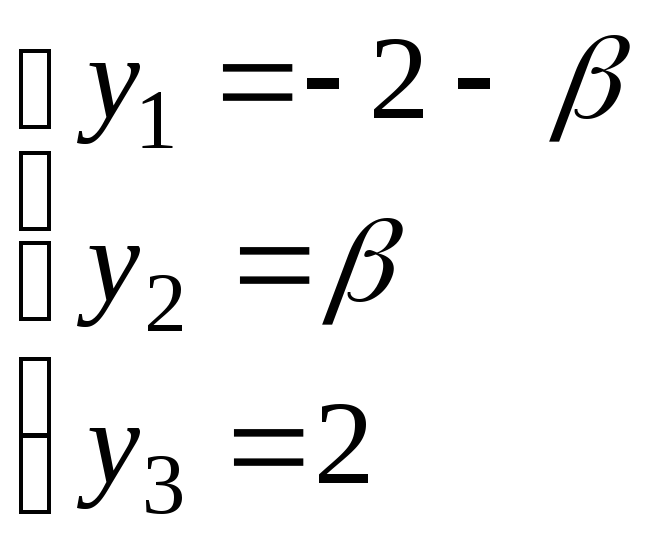 ,
где,R.
Тогда
,
где,R.
Тогда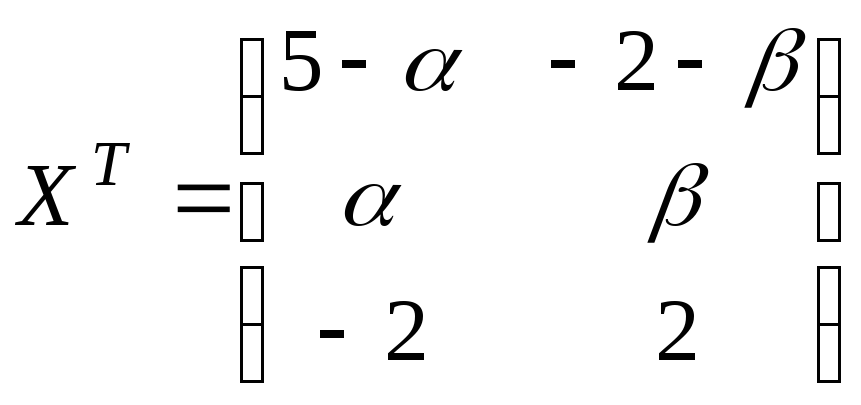 .Поэтому
.Поэтому
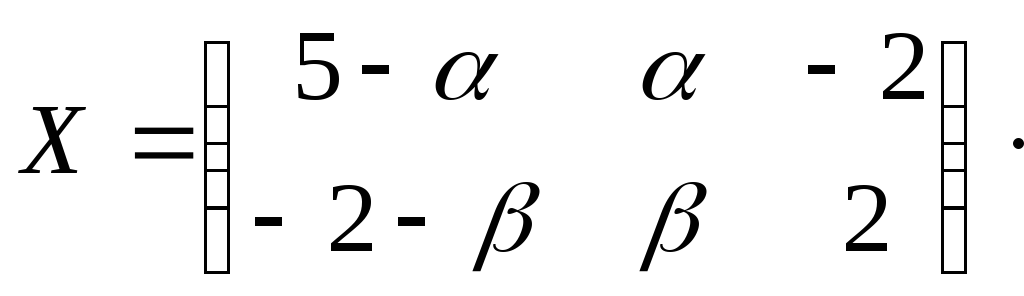
Проверка:![]()
![]()
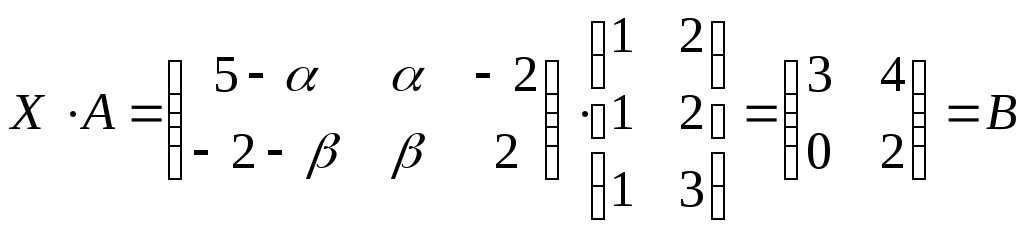
Ответ:а)Х=![]() б)Х=
б)Х=![]()
в) решения нет;
г) Х=![]() где
где![]() –
любые числа,
–
любые числа,
Задача 7Вычислить матрицы обратные данным:a)
 в)
в)
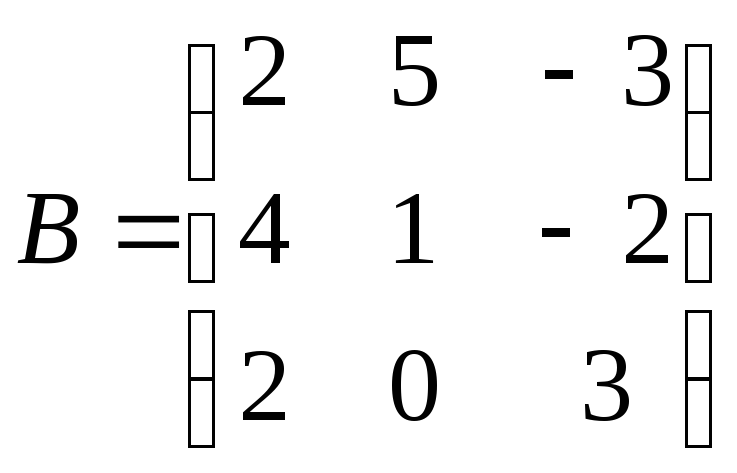
Решение.
а) Решим матричное
уравнение АХ=Е, как пакет систем
линейных уравнений: В
любой из трех систем пакета третье
уравнение противоречиво, т.e.
матрицаАне имеет обратной,
а, значит, вырождена.
В
любой из трех систем пакета третье
уравнение противоречиво, т.e.
матрицаАне имеет обратной,
а, значит, вырождена.
в) Решаем уравнение ВХ=Е, как пакет систем линейных уравнений:

![]()
![]()

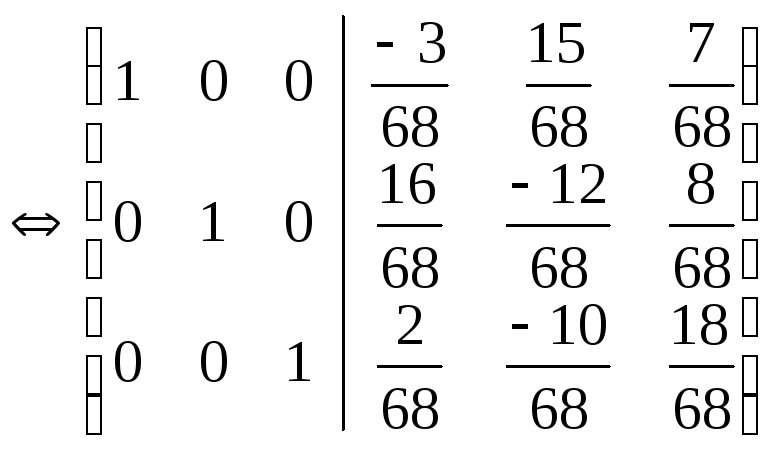
Тогда
X=
Проверка.
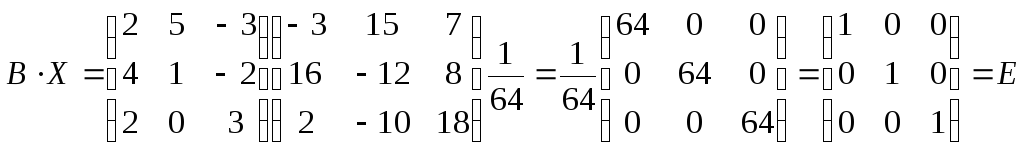
Значит, В–1=Х.
Замечание. Если для матрицы![]() существует обратная (матрица
существует обратная (матрица![]() невырождена), то для нахождения
невырождена), то для нахождения![]() составляется комбинированная
матрица
составляется комбинированная
матрица![]() которая при помощи элементарных
преобразований строк приводится к
виду
которая при помощи элементарных
преобразований строк приводится к
виду![]() где справа от черты искомая матрица
(способ элементарных преобразований
строк).
где справа от черты искомая матрица
(способ элементарных преобразований
строк).
Ответ: а) для
матрицы![]() –
обратной нет;
–
обратной нет;
б)
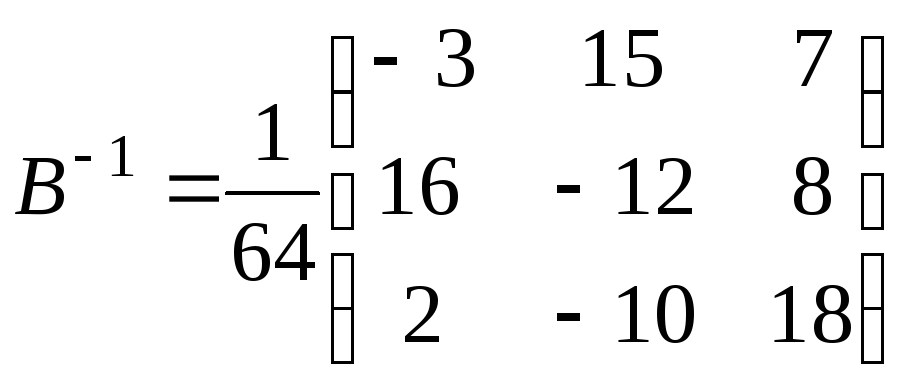
Для самостоятельного решения.
1. Перемножить
матрицы. Определить, существуют ли
оба произведения
![]() и
и![]() :
а)
:
а) ;
б)
;
б)
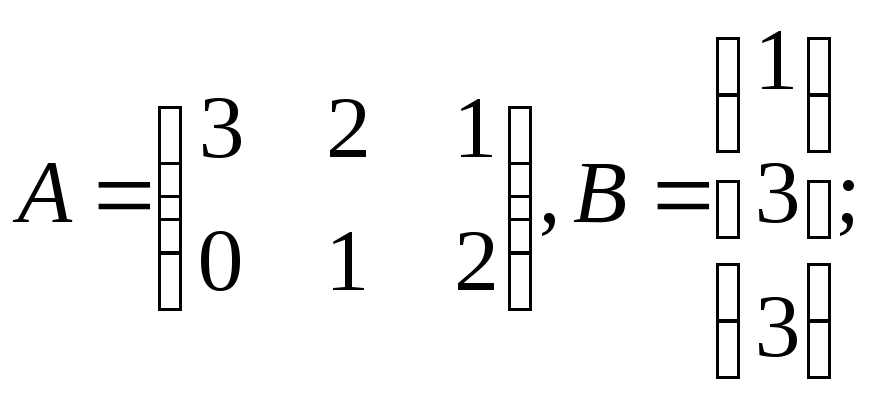 в)
в)
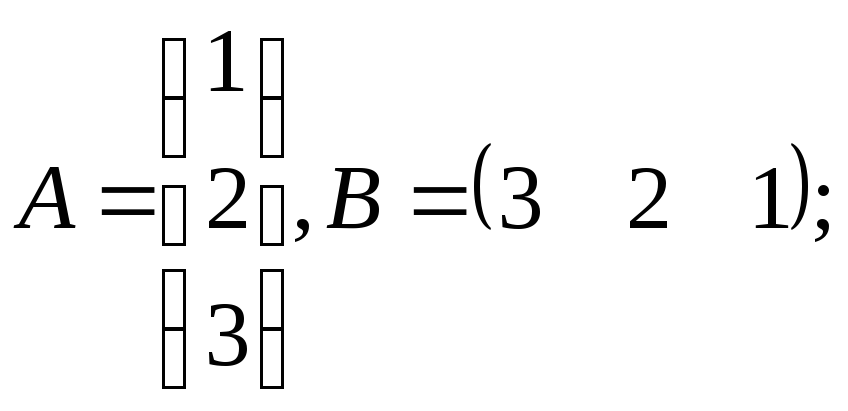 г)
г)
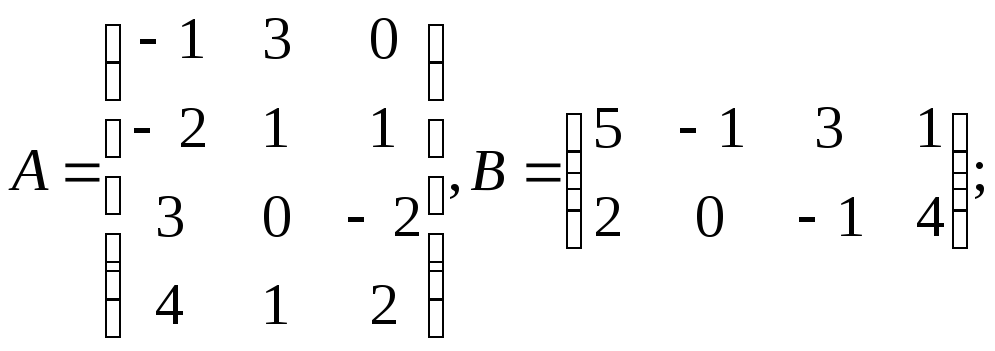 д)
д)
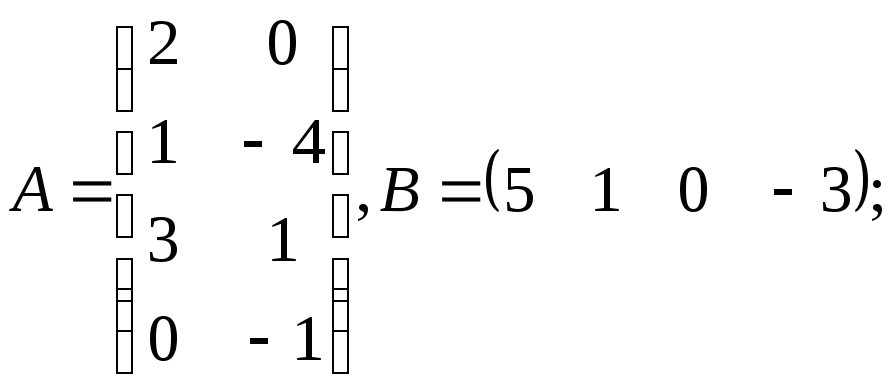 е)
е)
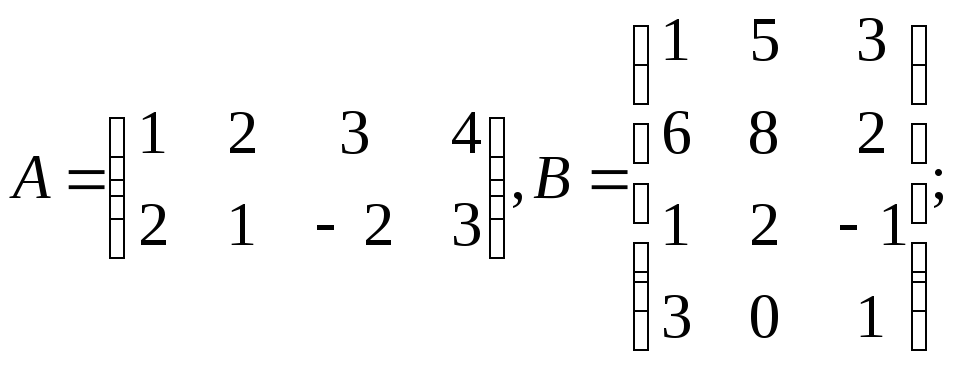 и)
и)
![]() к)
к)
![]() 2.
Вычислить
2.
Вычислить![]() если:
если:
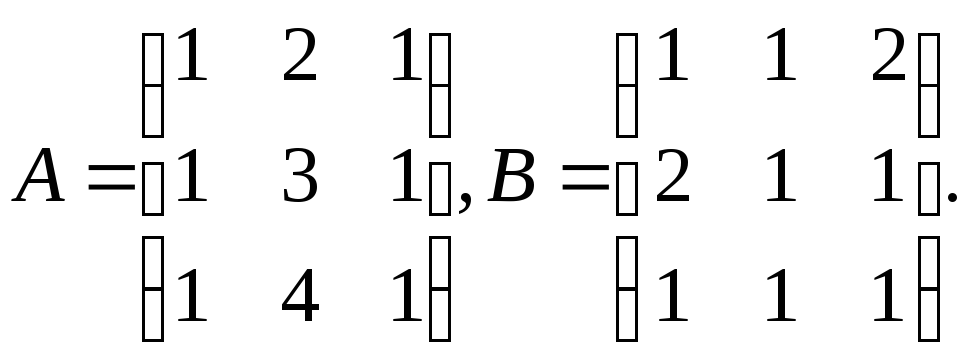 3.
Найти значение многочлена от
матриц:
a)
3.
Найти значение многочлена от
матриц:
a)![]()
![]() б)
б)![]()
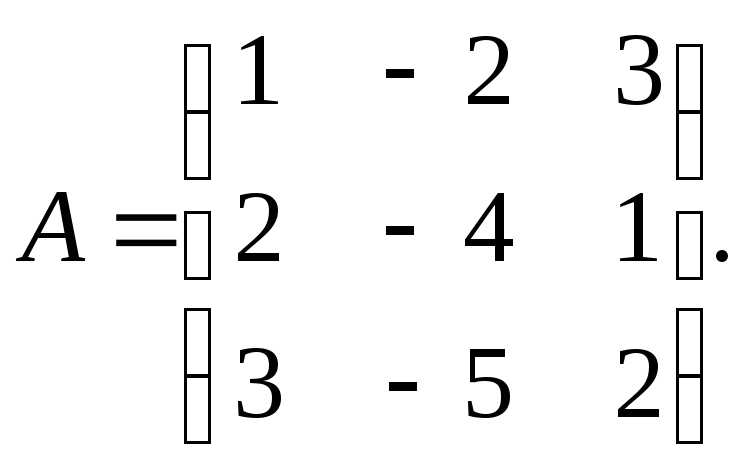 4.
Найти матрицы, обратные данным:
a)
4.
Найти матрицы, обратные данным:
a)![]() б)
б)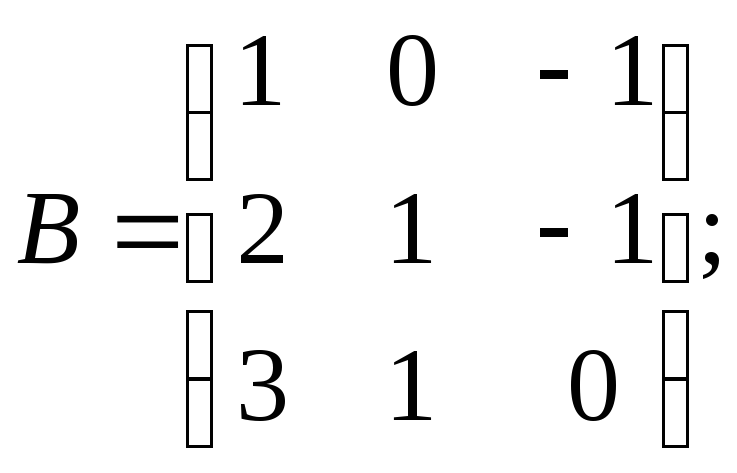 в)
в)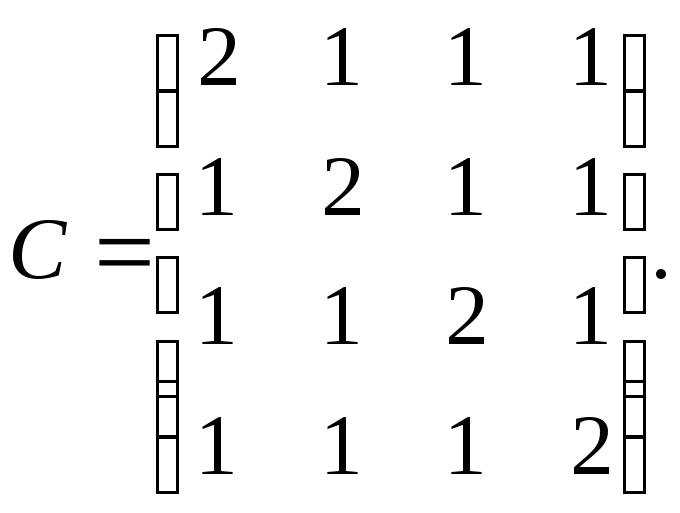 5.
Решите матричное уравнение:
а)
5.
Решите матричное уравнение:
а)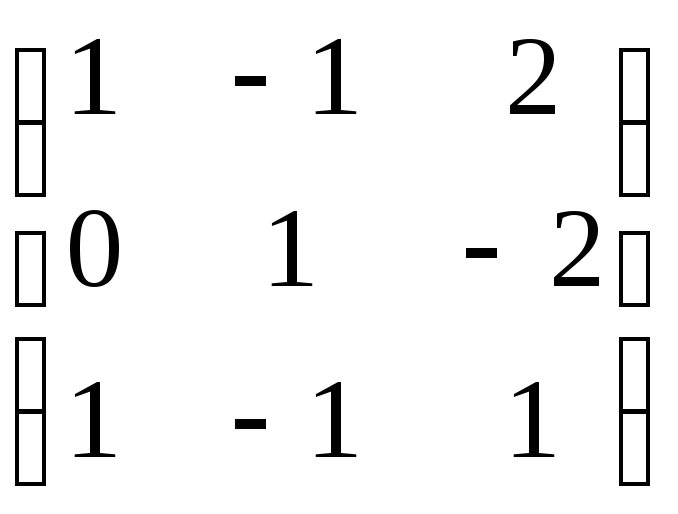 Х=
Х=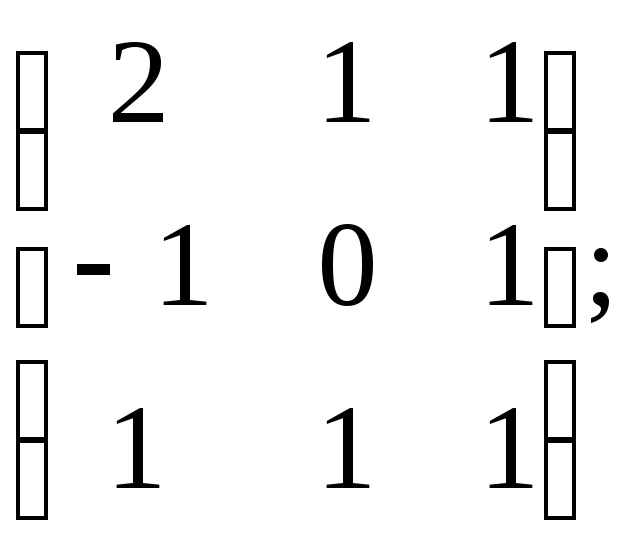 б)
б) Х=
Х=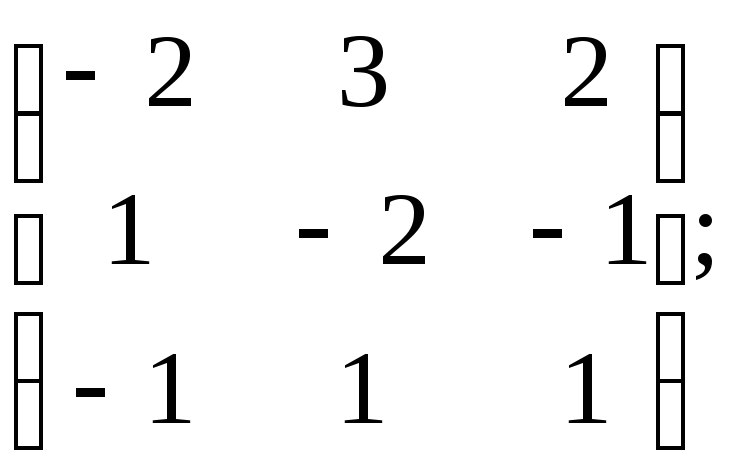 в)Х
в)Х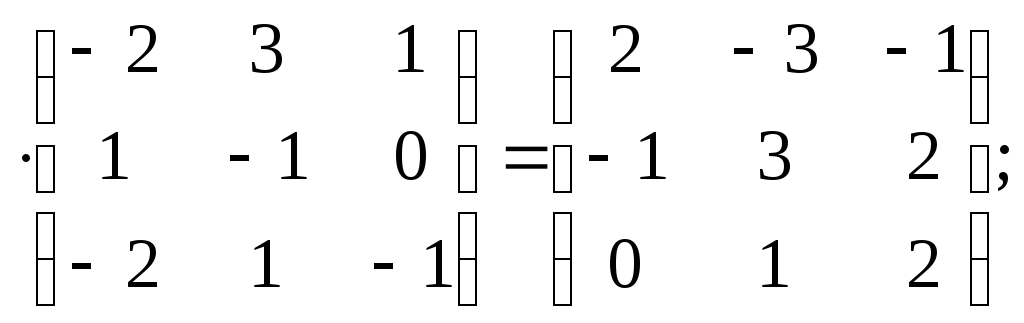 г)Х
г)Х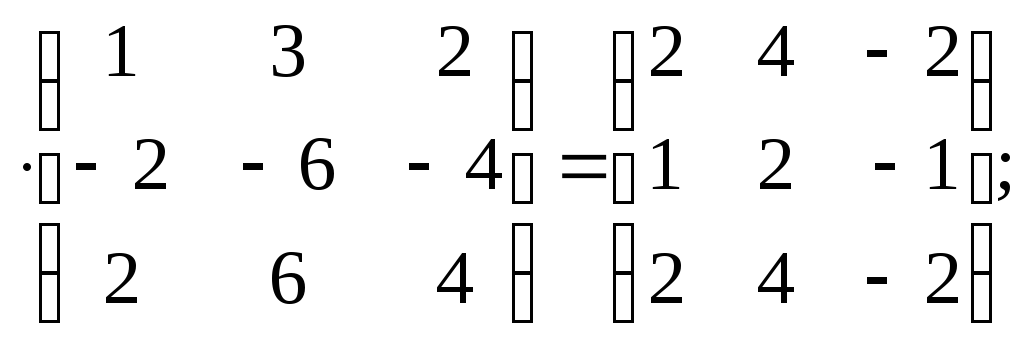 д)
д)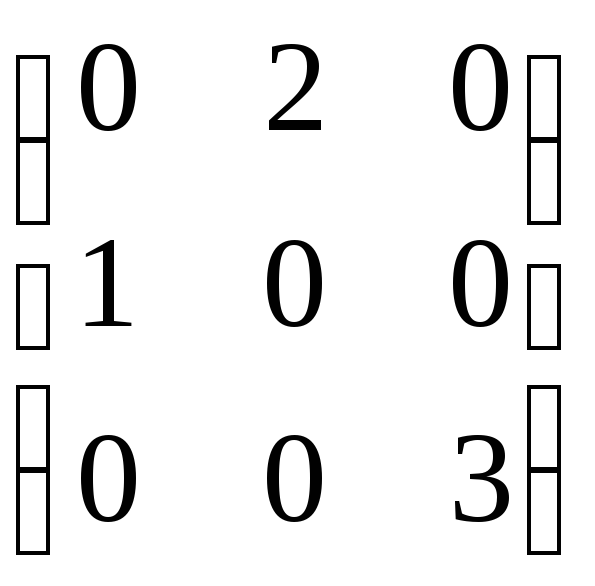 Х
Х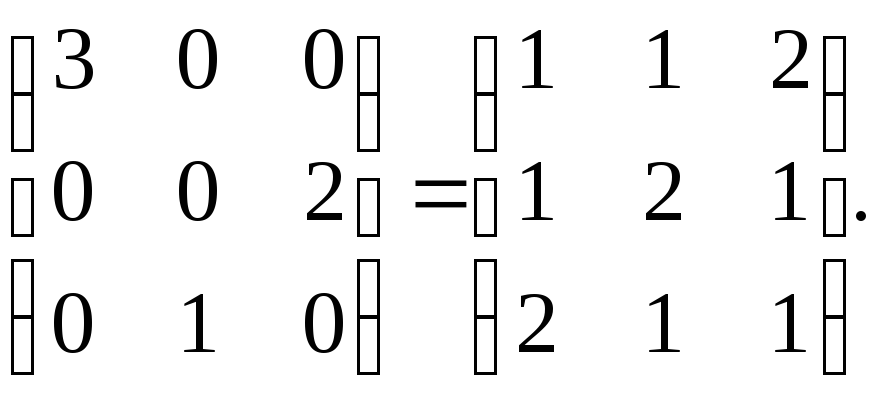 Указание.
В уравнении
Указание.
В уравнении![]() ,
обозначьте
,
обозначьте![]()
