
- •А л г е б р а
- •Глава 1. Системы линейных уравнений и арифметическое векторное пространство. §1. Системы линейных уравнений и их решение методом Гаусса.
- •§2. Арифметическоеn-мерное векторное пространство. Линейная зависимость и независимость. Базис и ранг системы векторов.
- •§3. Однородная система линейных уравнений. Фундаментальный набор решений.
- •Глава 2. Матрицы и определители. §4. Алгебра матриц.
- •§5. Определитель квадратной матрицы.
- •Глава 3. Комплексные числа. §6. Поле комплексных чисел.
- •§7. Уравнения третьей степени.
- •§8. Уравнения четвёртой степени.
- •Литература.
- •На молдавском языке.
§2. Арифметическоеn-мерное векторное пространство. Линейная зависимость и независимость. Базис и ранг системы векторов.
Определение арифметического вектора. Сложение векторов, умножение вектора на число. Свойства этих операций. Линейная комбинация векторов. Линейно зависимая и линейно независимы. Критерий линейной зависимости системы векторов. Базис и ранг системы векторов. Эквивалентные системы векторов и их свойства. Элементарные преобразования системы векторов.
Пусть Р={a,b,c,d…} – числовое поле, Pn={,,,…} – множество векторов. Арифметическим n–мерным вектором называется любой упорядоченный набор n чисел поля P, т.е. =( a1,a2,…,an), где aiP (i=1..n). Числа a1,a2,…,an , записанные в указанном порядке, называются координатами вектора.
Если =( a1,a2,…,an), =(b1,b2,…,bn) Pn, тогда определяют:
= a1=b1, a2=b2,..., an=bn;
+=(a1+b1,a2+b2,...,an+bn)
k=(ka1,ka2,…,kan), где kP.
Вектор =(0,0,...,0) Pn называется нулевым вектором. Вектор –=(–1)=(–a1,–a2,…,–an) называется противоположным вектору .
Операция сложения векторов из Pn обладает следующими свойствами:
, Pn +=+ (коммутативность);
, , Pn (+)+=++ (ассоциативность);
Pn += (–нейтральный элемент относительно операции сложения векторов);
Pn (–)Pn +(–)= ,где (–) является элементом симметричным элементу относительно операции сложения.
Операция умножения вектора на скаляр обладает следующими свойствами:
Pn 1=, где 1–единица поля P;
Pn a, bP a(b)=(ab).
Операция умножения вектора на скаляр связана с операциями сложения двумя дистрибутивными законами:
Pn a, bP (a+b) =a+b;
aP ,Pn a(+)=a+a.
Перечисленные свойства доказываются непосредственной проверкой.
Множество Pn всехn-мерных арифметических векторов, в котором определены операции сложения векторов и умножения вектора на элементы из поляP(указанным выше способом), называетсяn-мерным арифметическим векторным пространством над полем P.
Например, Rn – n-мерное арифметическое пространство, вектора которого имеют действительные координаты.
Условимся под системой векторов арифметического пространстваPnпонимать конечный упорядоченный набор векторов этого пространства.
Пусть 1,2,…,m– некоторая система векторов пространстваPn. Вектор=a11+a22+…+ammназываетсялинейной комбинацией векторовуказанной системы, числа1,2,…,m –коэффициентыэтойлинейной комбинации.Говорят также, что векторлинейно выражаетсячерез вектора1,2,…,m.
Если вектор линейно выражается через вектора системы1,2,…,m, а каждый из векторовIлинейно выражается через вектора системы1,2,…,k, то векторлинейно выражается через вектора1,2,…,k.
Линейная комбинация системы векторов называется нетривиальной, если хотя бы один её коэффициент отличен от нуля, итривиальной, если все её коэффициенты равны нулю.
Cистема векторов называется линейно зависимой, если существует ее нетривиальная комбинация, равная нулевому вектору.
Система векторов называется линейно независимой,если всякая ее линейная комбинация, равная нулевому вектору, тривиальная.
Система, состоящая из одного нулевого вектора, линейно зависима.
Теорема 1. (критерий линейной зависимости системы векторов). Система векторов линейно зависима тогда и только тогда, когда хотя бы один из ее векторов линейно выражается через остальные или она состоит только из нулевого вектора.
Вопрос о линейной зависимости можно свести к вопросу о наличии ненулевых решений у соответствующей системы линейных однородных уравнений. Рассмотрим, например, систему векторов:
1=(1,1,2);2=(–2,1,–1);3=(–1,2,1)
Выясним, при каких значениях коэффициентов ее линейная комбинация равна нулевому вектору. Пусть x11+x22+x33=
Распишем это
векторное равенство:
x11=(x1,x1,2x1)
+x22=(–2x2,x2,–x2)x33=(–x3,2x3,x3)
–––––––––––––––––
(
 0,0,0)==(x1–2x2–x3,x1+x2+2x3,2x1–x2+x3),
откуда
по определению равенства арифметических
векторов
0,0,0)==(x1–2x2–x3,x1+x2+2x3,2x1–x2+x3),
откуда
по определению равенства арифметических
векторов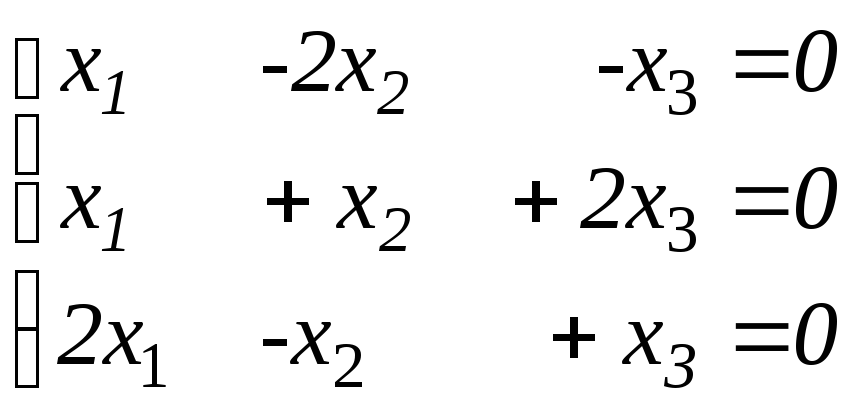 .
.
Решаем полученную
систему линейных уравнений методом
Гаусса:
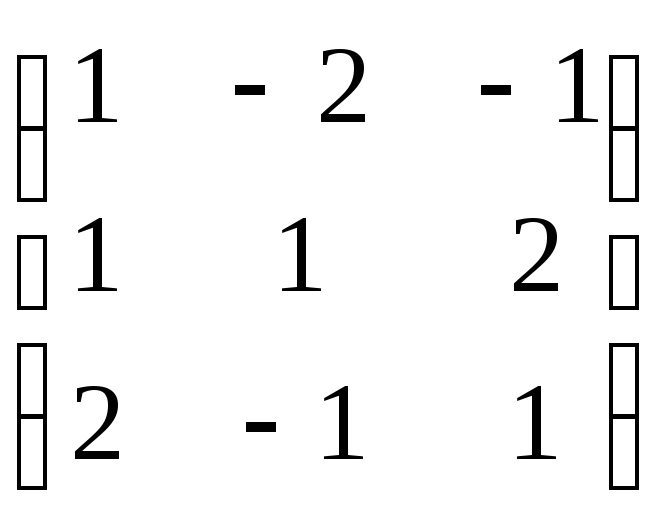
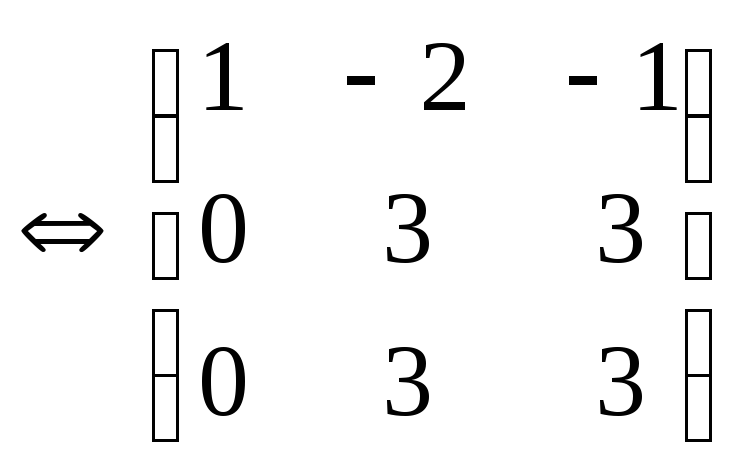
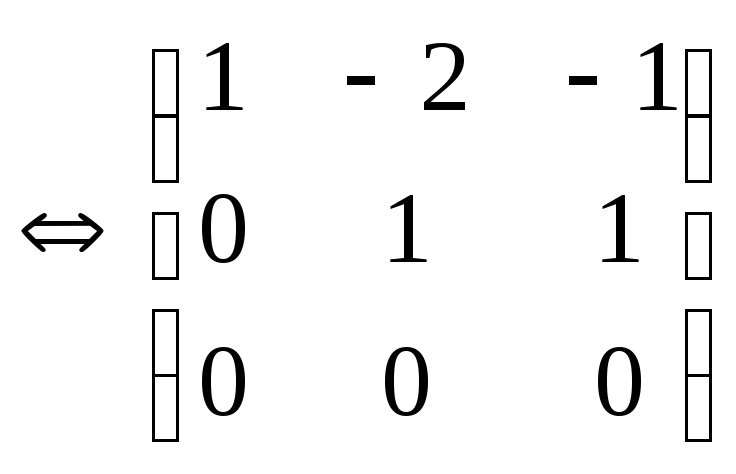
Cистема
уравнений является неопределенной и
имеет ненулевые решения. Следовательно,
данная система векторов линейно
зависима. Общее решение системы
имеет вид(–а,–a,a)aR,
и приа=–1 получаем частное
решение (1,1,–1). Тогда 11+12–13=.
Аналогичными рассуждениями доказывается линейная независимость системы единичных векторов: e1=(1,0,0,…,0),e2=(0,1,0,…,0), …………………en=(0,0,0,…,1), а также линейная независимость ступенчатой системы векторов, примером которой может служить система1=(a11,a12,…,a1r,…,a1n),2=( 0,a22,…,a2r,…,a2n),r=( 0, 0,…,arr,…,arn), где а11, а22, … ,arr0
Теорема 2. (основная теорема о линейной зависимости). Если система векторов1,…,kлинейно выражается через систему1,…,sиk>s, то первая система линейно зависима. Следовательно, всякая система изkn-мерных векторов приk>nлинейно зависима.
Базисом системы векторов называется такая ее линейно независимая (упорядоченная) подсистема, через которую линейно выражаются все вектора системы.
Система, состоящая только из нулевых векторов, базисом не обладает, так как в этом случае невозможно выделить ее линейно независимую подсистему. Линейно независимая система векторов сама является собственным базисом. У линейно зависимой системы может быть более одного базиса.
Две системы векторов называются эквивалентными,если каждая из них линейно выражается через другую.
Всякая система векторов эквивалентна своему базису, так как каждый вектор системы выражается, притом единственным образом, через базисные векторы1,…,kэтой системы в виде линейной комбинации=а11+…+akk. Набор (а1, а2, … ,ak) называют координатами вектора в базисе (1,2,… ,k). Любые два базиса одной и той же системы векторов также эквивалентны. К эквивалентным системам приводят ихэлементарные преобразования, к которым относятся:
умножение любого вектора системы на отличное от нуля число;
прибавление к одному из векторов системы другого вектора системы умноженного на число;
исключение из системы (включение в систему) вектора, являющегося линейной комбинацией остальных;
перестановка любых двух векторов системы.
Эквивалентность всех базисов одной системы векторов и основная теорема о линейной зависимости позволяют утверждать, что любые два базиса одной и той же системы векторов содержат одинаковое количество векторов.
Рангом системы векторов называется число векторов в ее базисе. Или иначе, ранг системы векторов — это максимальное число ее линейно независимых векторов.
У эквивалентных систем векторов эквивалентны базисы, поэтому эквивалентные системы векторов имеют одинаковые ранги. Следовательно, элементарные преобразования системы векторов не изменяют ее ранга.
Все изложенное относится и к арифметическим векторам над нечисловыми полями, с той лишь разницей, что везде вместо число следует говорить “ элемент поля Р”.
Задача 1. Найти линейную комбинацию=21–42+53системы векторов1=(2,1,2,1);2=(–3,1,5,4);3=(3,2,0,1).
Решение. Используя определения произведения числа на вектор и суммы векторов, получаем
21= (4,2,4,2)
+ –42= (12,–4,–20,–16)
 53=
(15,10,0,5)
53=
(15,10,0,5)
= (31,8,–16,–9)
Ответ:= (31,8,–16,–9).
Задача 2. Выяснить, зависима или независима система векторов, найти один из ее базисов и вычислить ранг, выразить небазисные векторы через выбранный базис:1=(2,1,–1,3);2=(–1,3,–2,1);3=(1,2,3,–1);4=(1,12,5,–1);5=(5,0,13,–5);
Решение. I cпособ. Следует выяснить при каких значенияхх1,x2,x3,x4,x5, имеет место равенство:
x11+x22+x33+x44+x55=0 (1)
Запишем векторное равенство (1) в виде системы однородных линейных уравнений:
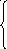 2x1
–x2
+x3
+x4+
5x5=0
x1+3x2+2x3+12x4
=0
(2)
–x1
–2x2+3x3
+5x4+13x5=0
3x1+x2
–x3
–x4
–5x5=0
2x1
–x2
+x3
+x4+
5x5=0
x1+3x2+2x3+12x4
=0
(2)
–x1
–2x2+3x3
+5x4+13x5=0
3x1+x2
–x3
–x4
–5x5=0
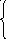 Решаем
систему (2) методом Гаусса:
Решаем
систему (2) методом Гаусса:

![]()
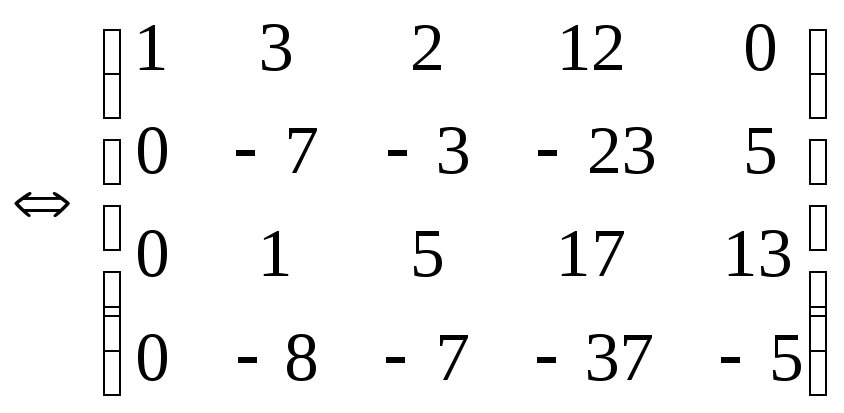
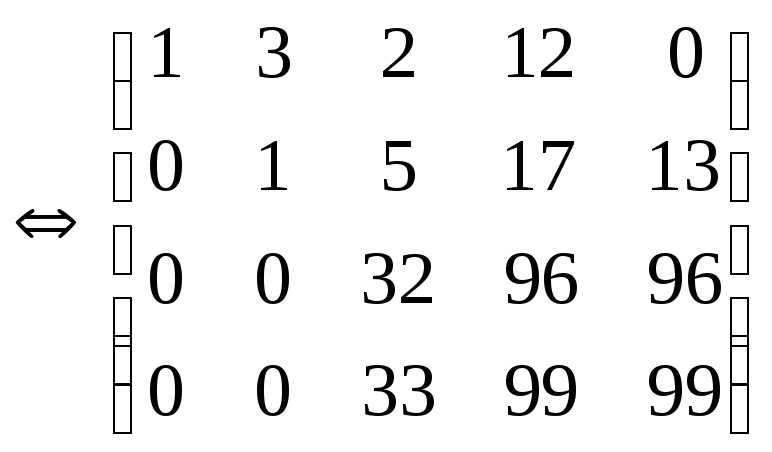
 x1+3x2+2x3+12x4
=0x2+5x3+17x4
+13x5=0x3+3x4+
3x5
=0гдех1,x2,x3
– главные неизвестные;х4,х5–свободные
неизвестные.x1=–3(–2а+2b)–2(–3а–3b)–12а=0,x2=–5(–3а–3b)–17а–13b=–2а+2b,x3=–3а–3b,x4=
а,x5=b.
x1+3x2+2x3+12x4
=0x2+5x3+17x4
+13x5=0x3+3x4+
3x5
=0гдех1,x2,x3
– главные неизвестные;х4,х5–свободные
неизвестные.x1=–3(–2а+2b)–2(–3а–3b)–12а=0,x2=–5(–3а–3b)–17а–13b=–2а+2b,x3=–3а–3b,x4=
а,x5=b.
Общее решение системы (2): {(0,–2а+2b,–3a–3b,a,b)a,bR}. Таким образом, система (2) имеет ненулевые решения, следовательно, система векторов1,2,3,4,5– линейно зависимая.
Векторы 1,2,3, соответствующие по номерам главным неизвестнымx1,x2,x3 , образуют базис. Докажем это. Подставим в (1) найденное решение: 01+(–2а+2b)2+(–3a–3b)3+a4+b5=(3)
Покажем, что система 1,2,3линейно независима. Для этого рассмотрим равенство
y11+y22+y33=(4) илиy11+y22+y33+04+05=(5) Так как (5) содержится в (3), то
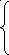
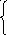 y1=0
y1=0
y2=–2а+2by1=0
y3= –3a–3b или y2=0 (6)
0=ay3=0
0=b
Итак, равенство (4) выполняется только при условии (6). Следовательно, система 1,2,3, линейно независима.
Покажем, что все векторы системы 1,2,3,4,5выражаются через векторы1,2,3.Пологая в (3) а =1, b=0, получим4=01+22+33; при а=0,b=1, получим5=01– 22+33.
![]()
II
cпособ. Элементарными преобразованиями
систему1,2,.3
,4,5приведем к лестничному виду. Для
этого выпишем матрицу координат
векторов-строк и проведем элементарные
преобразования системы ее строк:![]()
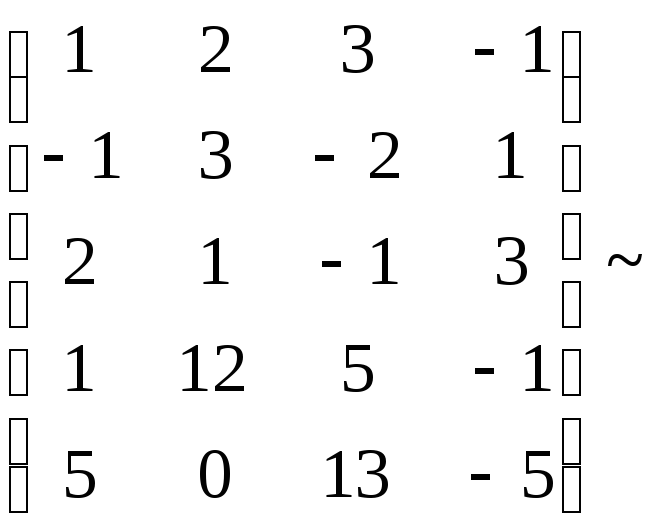
 ~
~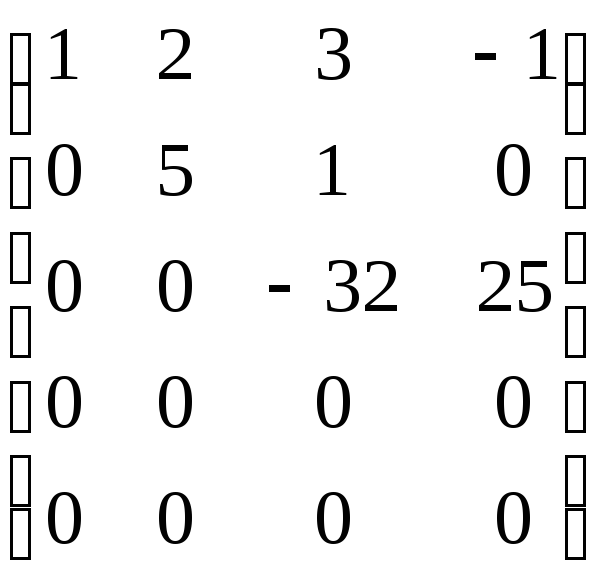
Преобразования осуществлялись только с помощью первых трех строк, а четвертая и пятая строки аннулировались, следовательно, можно утверждать, что 4 и5 линейно выражаются через1,2,3. Кроме того, система векторов1,2,3линейно независима, так как эквивалентная ей система из первых трех строк последней матрицы линейно независима, ибо имеет лестничный вид. Итак,1,2,3образует базис системы1,2,3,4,5, ранг которой равен 3.
Для вычисления коэффициентов линейных комбинаций 4=x11+x22+x33;5=y11+y22+y33, запишем их в виде систем линейных уравнений:
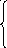
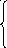 2x1
–x2
+x3=1
2y1–y2+
y3
=5
x1+3x2
+2x3=12
, y1+3y2+2y3=0
–x1
–2x2+3x3=5 –y1–2y2+3y3=13
3x1+x2
–x3=–1 3y1+y2
–y3=–5.
2x1
–x2
+x3=1
2y1–y2+
y3
=5
x1+3x2
+2x3=12
, y1+3y2+2y3=0
–x1
–2x2+3x3=5 –y1–2y2+3y3=13
3x1+x2
–x3=–1 3y1+y2
–y3=–5.
Эти системы
отличаются только обозначениями
неизвестных и столбцами свободных
членов, поэтому их можно решать
одновременно, записав рядом два
столбца свободных членов (пакет двух
систем линейных уравнений):
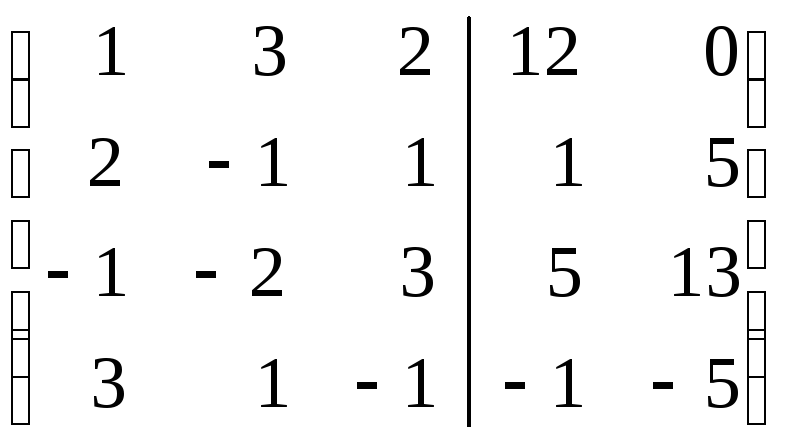

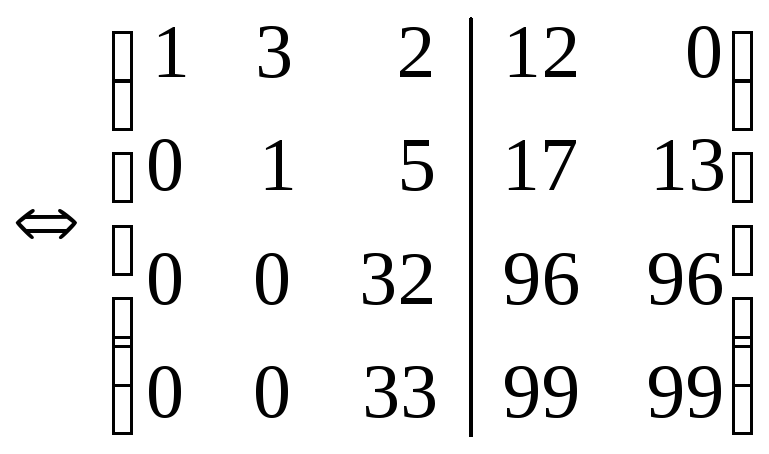
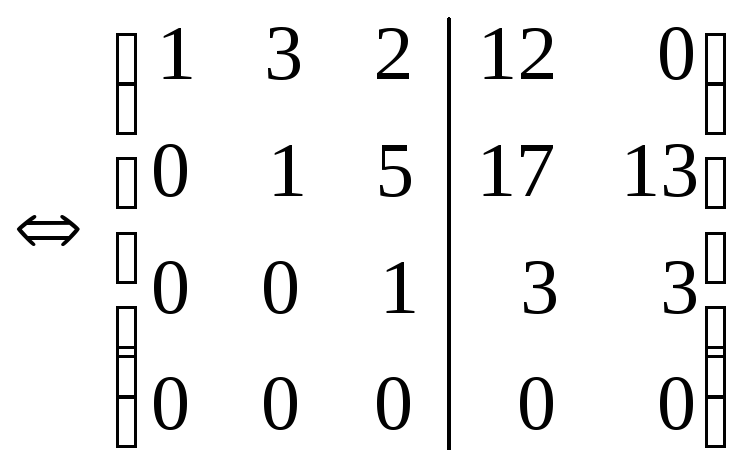
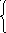
 x1+3x2+2x3=12x1=0x2+5x3=17
,x2=2x3=3x3=3.
x1+3x2+2x3=12x1=0x2+5x3=17
,x2=2x3=3x3=3.
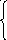
 y1+3y2+2y3=0
y1=0
y2
+5y3=13
, y2=–2
y3=3
y3=3.
y1+3y2+2y3=0
y1=0
y2
+5y3=13
, y2=–2
y3=3
y3=3.
4=01+22+33,5=01–22+33.
Ответ:система векторов линейно зависима, один из ее базисов1,2,3, ранг системы равен 3,4=01+ 22+33,5=01–22+33.
Задача 3.Пользуясь элементарными преобразованиями установить линейную зависимость или независимость системы векторов:1= (1,–2,2);2=(2,0,1);3=(–1,–3,4).
Решение.
Элементарные преобразования
приводят к системе эквивалентной
данной. Преобразуем по методу Гаусса
матрицу координат-сток данных
векторов
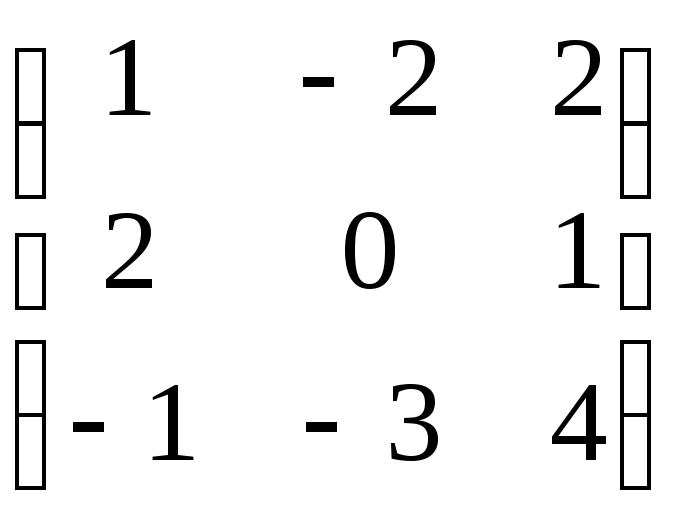 ~
~
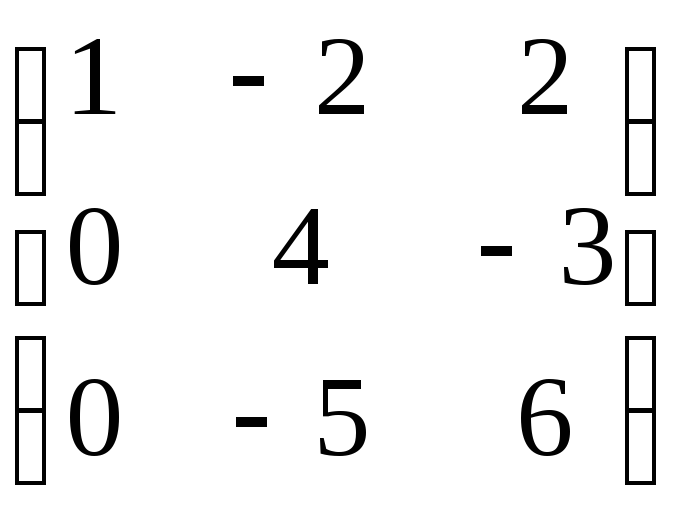 ~
~
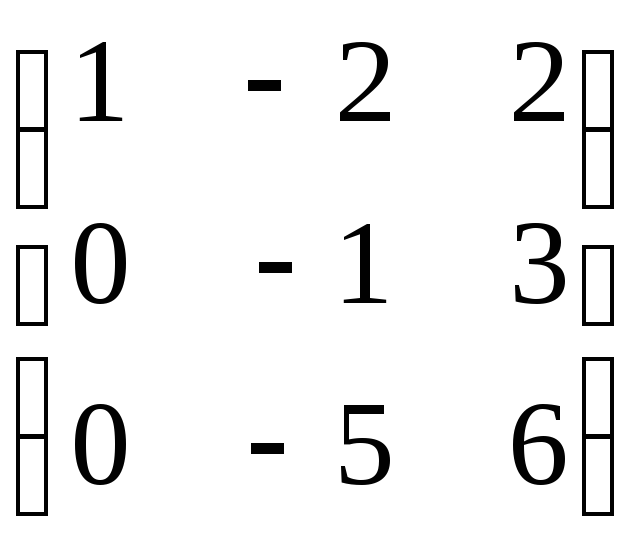 ~
~
Система 1=(1,–2,2),2=(0,–1,3) ,3=(0,0,–9) эквивалентна данной системе и линейно независима (как лестничная система). Ранг полученный системы равен 3. Следовательно, система1,2,3– линейно независима.
Ответ. Система векторов1,2,3–линейно независима.
Для самостоятельного решения.
1. Найти вектор, если 3(1–2)+5(2+3–3)=2(3–4) и1=(4,3,1,2),2=(2,–1,–3,4),3=(–1,4,–5,3).
2.Выясните линейную зависимость или независимость системы векторов. Найдите какой-нибудь базис системы, укажите ее ранг. Выразите небазисные векторы через базисные: а) (1,–1,1,–1), (1,0,1,0), (1,–3,1,–3); б) (1,2,–1,0,3), (1,1,–1,3,–3), (2,3,2,–1,4), (1,5,–1,–9,21), (2,3,0,1,2); в) (1,1,1,1,1), (1,2,3,4,1), (2,1,3,4,5), (1,2,–1,4,3).
3.Докажите, что приs>nлюбыеsn-мерных векторов линейно зависимы.
