51

§1. . . . решение методом Гаусса. . . .

А л г е б р а

(1 часть)

Тирасполь 2002г.

Составители: канд. педагогических наук, доцент кафедры алгебры и геометрии Ермакова Г.Н., старший преподаватель кафедры математического анализа и методики преподавания математики Драганов А.В.

Рекомендовано к кафедральному изданию заседанием Научно-методического совета ПГУ им.Т.Г.Шевченко 03.04.02г. протокол №8.

Рецензенты: Ю.М. Рябухин, доктор физико-математических наук, академик АНМ;

А.Д. Герасимова, кандидат педагогических наук, доцент кафедры математического анализа и методики преподавания математики ПГУ

Настоящий задачник-практикум предназначен для студентов первого курса физико-математического факультета Является пособием для самостоятельного овладения методами и способами решения задач по разделам: «Системы линейных уравнений и арифметическое векторное пространство», «Матрицы и определители», «Комплексные числа», - в объёме действующей программы курса алгебры. Пособие содержит теорию (обзорно), образцы решения задач, задачи для самостоятельного решения.

Глава 1. Системы линейных уравнений и арифметическое векторное пространство. §1. Системы линейных уравнений и их решение методом Гаусса.

Линейное уравнение. Вид противоречиво линейного уравнения. Общий вид cистемы линейных уравнений. Множество решений. Равносильные сис­темы. Следствие системы. Элементарные преобразования системы линейных уравнений. Метод Гаусса решения систем линейных уравнений. Распределение неизвестных на главные и свободные.

В общем виде линейное уравнение (уравнение первой степени) запи­шется в виде:

a₁x₁+a₂x₂+...+a_nx_n=b, (1)

где a₁,a₂,...,a_n,b– фиксированные числа (коэффициенты при неизвестных и свободных член). Не исключается случай, когда уравнение имеет вид:

0x₁+0x₂+...+0x_n=b. (2)

Решением уравнения(1) называется любой упорядоченный набор (l₁,l₂,...,l_n ) ( вектор=(l₁,l₂,...,l_n) ) чиселl₁,l₂, ,...,l_n, таких, что при подстановке их вместо соответствующих неизвестных уравнение обращается в верное чис­ловое равенство

a₁l₁+a₂l₂+...+a_nl_n=b.

Очевидно, что при b=0 уравнению (2) удовлетворяет любой набор значений неизвестных, а приb0 не удовлетворяет ни один набор значений. Приb=0 уравнение (2) назовемтождественным, а приb–противоречи­вым.

Если даны mлинейных уравнений с неизвестнымиx₁,x₂,...,x_n и требу­ется найти общие решения всех уравнений, то в этом случае говорят о сис­темеmлинейных уравнений сnнеизвестными (системаS). Такую систему записывают в виде:

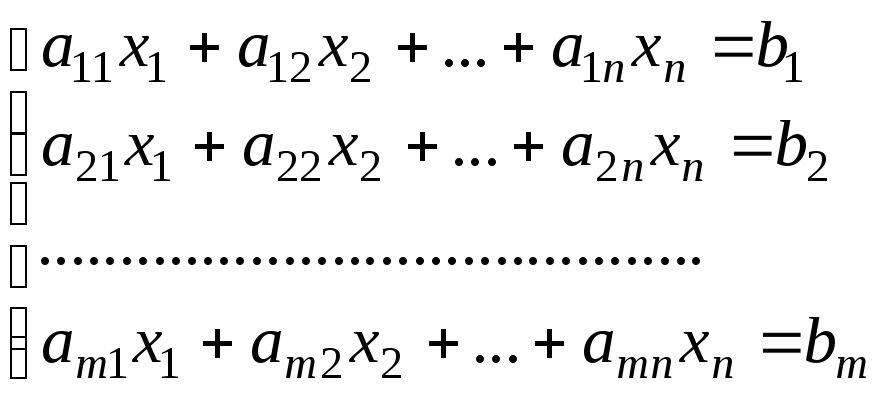
(3)

Решением системы(3) называется упорядоченный набор (l₁,l₂,...,l_n ) (вектор=(l₁,l₂,...,l_n)) чиселl₁,l₂,...,l_n .

Cистема называетсясовместной, если она имеет хотя бы одно реше­ние , инесовместной , если она не имеет ни одного решения.

Для любой системы возможны только три случая:

1. система несовместна;

2. система имеет единственное решение (совместно определенная);

3. система имеет бесчисленное множество решений (совместно неопре­деленная).

Промежуточный случай, когда решений конечное число, притом больше чем одно, невозможен.

Система S₂называетсяследствием системы S₁, если всякое решение системыS₁является решением системыS₂ или еслиS₁ несовместна.

Понятно, что всякая часть линейной системы, в том числе и одно от­дельно взятое уравнение, будет ее следствием.

Две линейные системы называются равносильными,если каждая из них является следствием другой, т.e. системы равносильны, если множества их решений совпадают.

В процессе решения системы проводятся такие ее преобразования, ко­торые не изменяют множества решений. В частности система заменяется равносильной при выполнении элементарных преобразований, к которым относятся:

1. перестановка двух уравнений системы;

2. вычеркивание уравнения вида 0х₁+0х₂+…+0x_n=;

3. умножение какого-либо уравнения системы на число, отличное от нуля;

4. прибавление к одному уравнению системы другого ее уравнения, умноженного на некоторое число.

Универсальным методом решения линейных систем является метод по­следовательного исключения неизвестных (метод Гаусса).

Рассмотрим систему (3). Если она содержит уравнение вида (2) и b≠0, то множество решений пусто. Процесс решения на этом закончен. Если в уравнении (2)b=0, то его можно удалить из системы, не изменяя множества решений. Поэтому можно считать, что в каждом уравнении исходной сис­темы хотя бы один из коэффициентов при неизвестных отличен от нуля. Пустьа₁₁≠0 (в противном случае поменяем местами уравнения или перену­меруем неизвестные). Исключим теперьx₁из всех уравнений, начиная со второго. Для этого ко второму уравнению прибавим первое, умноженное на–а₂₁/ а₁₁, затем к третьему уравнению прибавим первое, умноженное на–а₃₁/а₁₁, и т.д, к последнему уравнению прибавим первое, умноженное на –а_m1/a₁₁. В результате этой серии элементарных преобразований получим сис­тему:

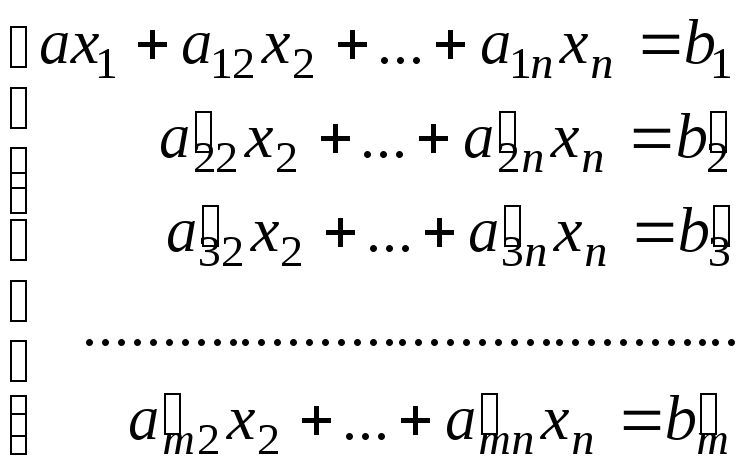(4) равносильную исходной. Удалим из системы (4) нулевые уравнения (в связи с этим, в процесcе решения системы число уравнений может уменьшиться). Если хотя бы одно из уравнений системы (4) является противоречивым, то эта система и, следовательно, исходная несовместны.

Далее предположим, что 0, и продолжим процесс исключения неиз­вестных . Поскольку число таких шагов не превышаетn( числа неиз­вестных ), после конечного числа преобразований получим систему вида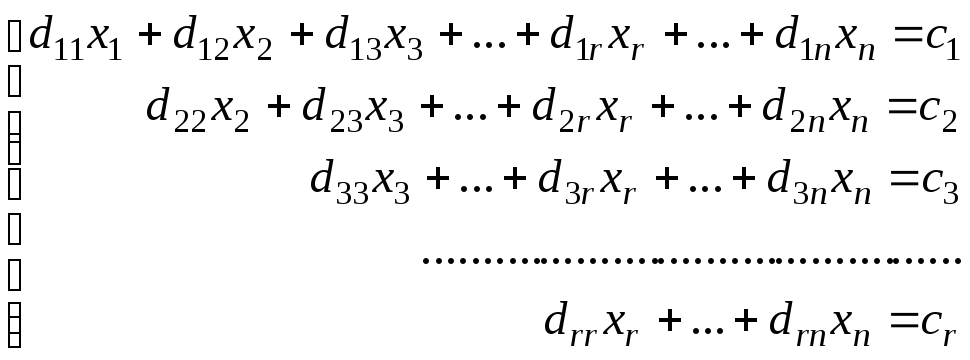(5) ( где «диагональные» коэффициентыd₁₁ , d₂₂ ,d₃₃ ,…, d_rr , rn, отличны от нуля), равносильную исходной системе (3).

Если r=n( в этом случае говорят, что система (5) имеет треугольный вид ), то из последнего уравнения находим значение неизвестнойx_n: x_n=c_n/d_nn. Подставив значениеx_nв предпоследнее уравнение, получим значе­ние неизвестнойx_n–1и т.д., т.е. идя снизу в верх, найдем значения всех неизвестных.

Итак, в случае r=n решение системы (5) (а значит , и (3)) единст­венно.

Если r<n( в этом случае говорят , что система (5) имеет вид трапе­ции ), то неизвестныеx₁,x₂,…,x_r(их называютглавными) можно выразить черезx_r+1 ,x_r+2 ,…, x_n . Неизвестныеx_r+1,x_r+2,…,x_n называютсвободными, так как, выбрав произвольным образом их значенияx_r+1=l_r+1, x_r+2=l_r+2,… x_n=l_n, одно­значно находим значения главных неизвестных x₁=l₁,x₂=l₂,…,x_r=l_r кото­рые в совокупности дают решение (l₁,l₂,…,l_r,l_r+1,…,l_n)исходной системы уравнений. Любое решение системы (3) можно получить таким образом. Сис­тему, в ко­торой главные неизвестные выражены через свободные, можно рас­сматривать какобщее решение исходной системы, т.е. как характеристиче­ское свойство множества ее решений.

Таким образом, в случае r<n система имеет бесконечное множество решений.

Итог сказанному можно подвести с помощью следующей теоремы.

Теорема.Если система линейных уравнений совместна, то с помощью элементарных преобразований ее можно привести к системе (5) с неравными нулю коэффициентамиd₁₁,d₂₂,…,d_rr; в противном случае эти преобразования позволяют получить из системы уравнение вида (2), гдеb – число, отличное от нуля.

Задача 1. Решить систему уравнений:

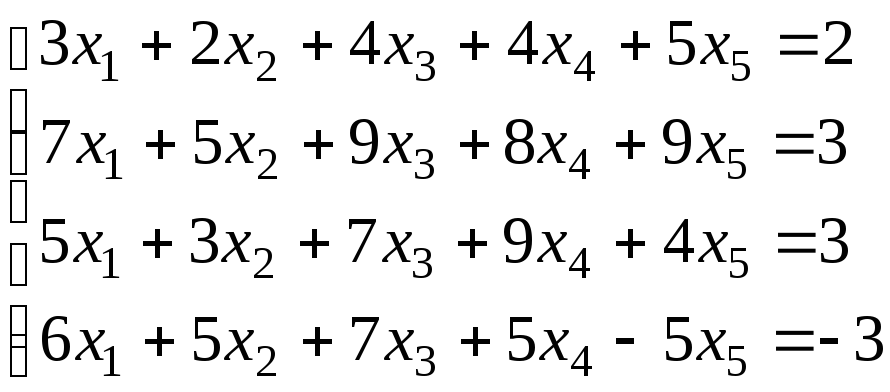
Решение. Если условиться писать неизвестные только в порядке воз­растания номеров, то сами символы неизвестных становятся лишними, важны лишь коэффициенты. Поэтому систему линейных уравнений удобно записы­вать и решать в виде расширенной матрицы, т.е. в виде прямоуголь­ной таб­лицы коэффициентов (вертикальной чертой отделены свободные члены).

Выписываем расширенную матрицу системы и проводим прямой ход схемы Гаусса (пояснения приведены ниже):

Чтобы получить единицу в верхнем левом углу матрицы, первую строку умножаем на 2 и вычитаем из нее третью. Полученную новую строку, умноженную на (–7), (–5) и (–6) соответственно, прибавляем ко вто­рой, третьей и четвертой строкам. Результатам этих операций является вторая из написанных матриц. Далее, четвертую строку умножаем на (–1) и пере­ставляем ее со второй, и прибавляем эту новую вторую строку , умноженную на 2 , к третьей и четвертой строкам ; результат – третья матрица. Теперь тре­тью строку умножаем на (–1/7), полученную новую третью строку, умножен­ную на 8, прибавляем к четвертой. Прямой ход закончен.

Выписываем систему, соответствующую последней матрице:

Проведем обратный ход. Здесь главные неизвестные x₁,x₂,x₄; свободные –х₃, х₅, придаем им произвольные значения:х₃=a, x₅=b. Двигаясь по послед­ней системе снизу вверх, выражаем главные неизвестные через свободные.

Запись обратного хода целесообразно вести так. Запишем заготовку ответа:

x₁=

x₂=

x₃=

x₄= затем будем вписывать в нее произвольные значения неизвестных

x₁=

x₂=a

x₃=

x₄=bи далее последовательно получаем значения остальных неизвестных:

x₁=1–(–13+a+36b)–a+(–2+7b)–6b=12–2a–35b,

x₂=9+a+11(–2+7b)–41b=–13+a+36b,

x₃=a,

x₄=–2+7b,

x₅=b, гдеa, b – любые числа.

Ответ: (12–2a–35b, –13+a+36b, a, –2+7b, b)

Задача 2.Решить систему уравнений

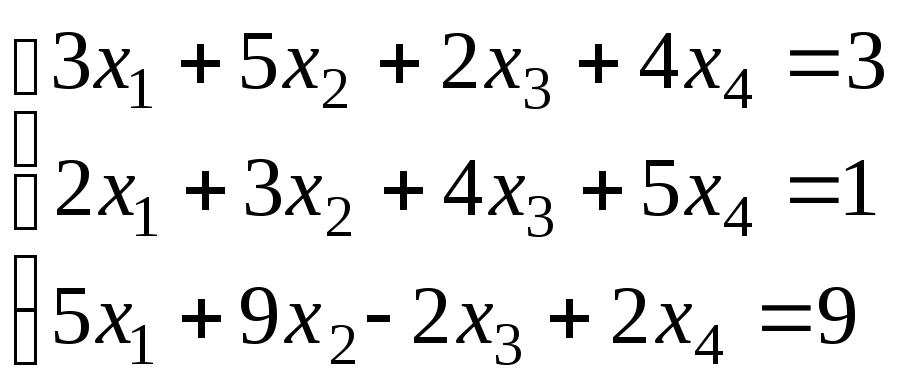
Решение.В расширенной матрице сначала вычитаем вторую строку из первой, чтобы получить единицу в верхнем левом углу матрицы, а затем но­вой первой строкой получаем нули в 1-м столбце; далее, из новой третьей строки вычитаем новую вторую: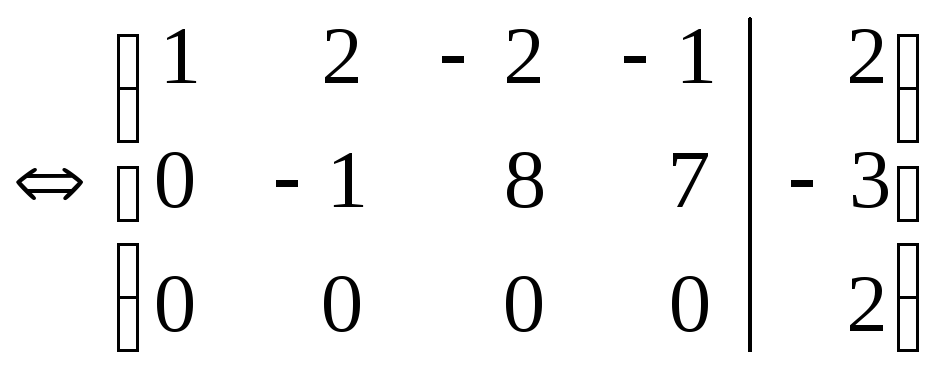Последняя строка последней матрицы даёт уравнение 0=2, не имеющее решений. Значит, система несовместна.

Ответ:система несовместна.

Задача 3.Решить систему уравнений

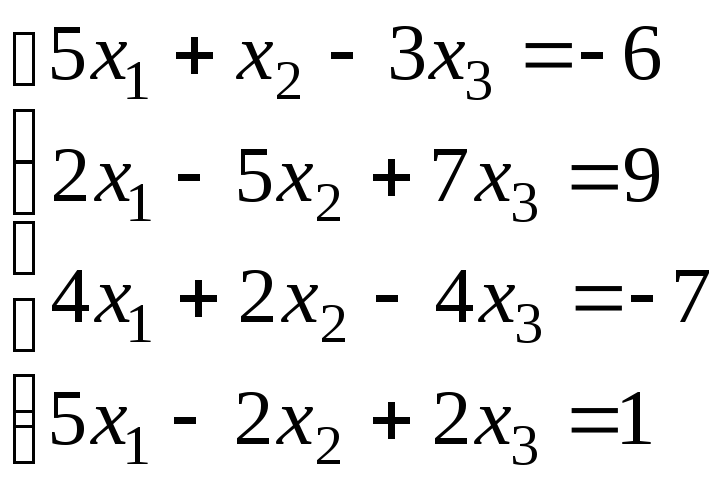
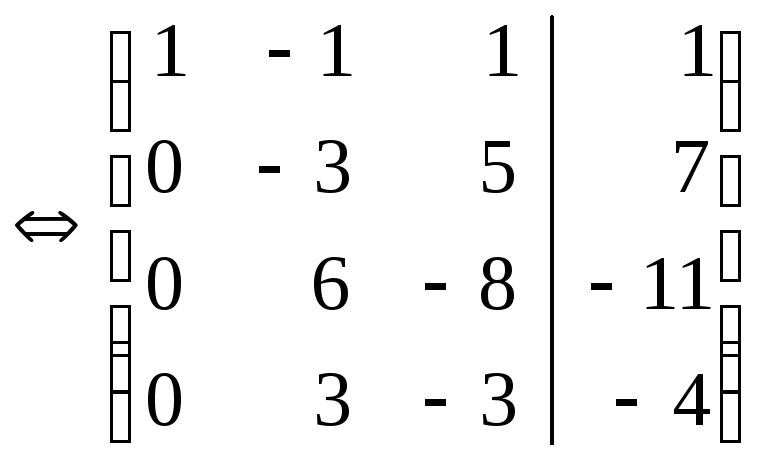
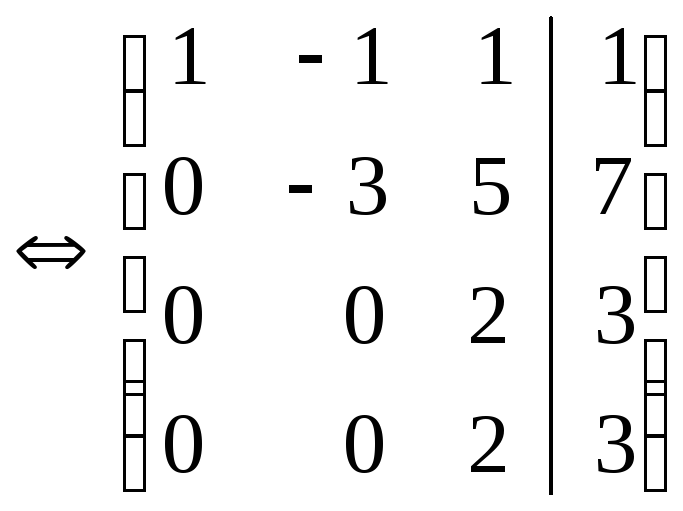
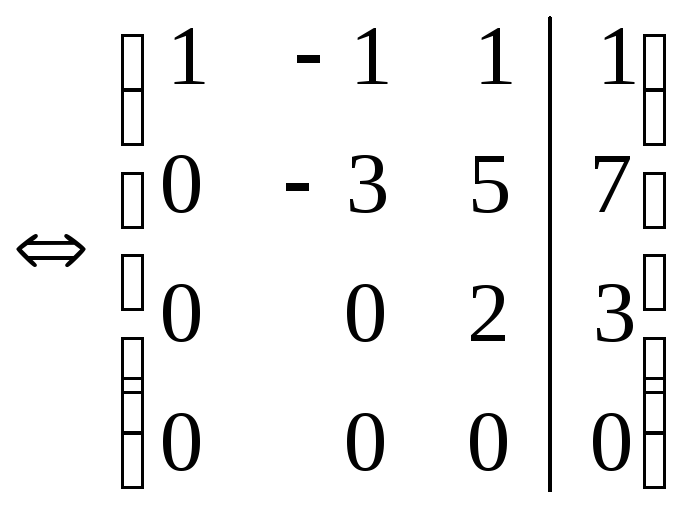
Решение.В расширенной матрице из первой строки вычитаем третью и получаем этой строкой нули в первом столбце, далее, второй строкой по­лучаем нули во втором столбце и т.д.: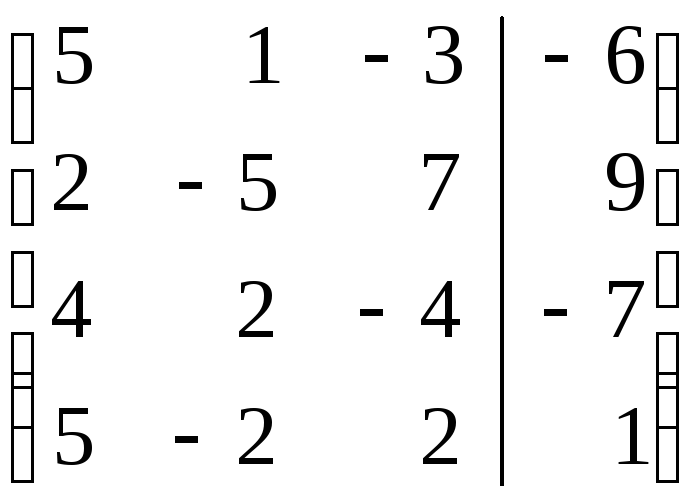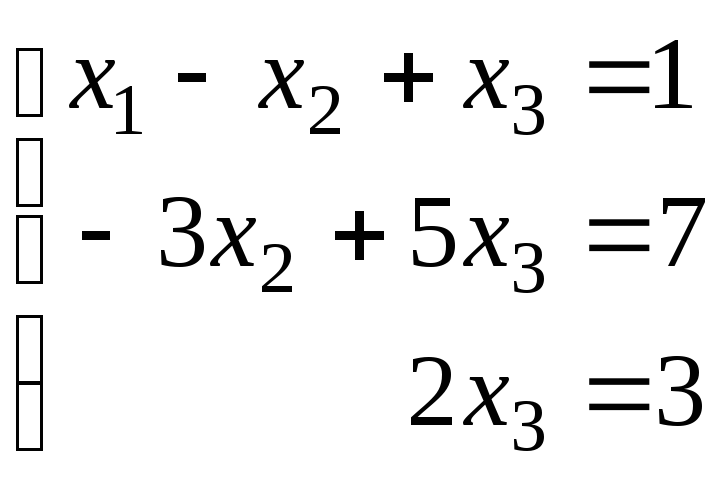,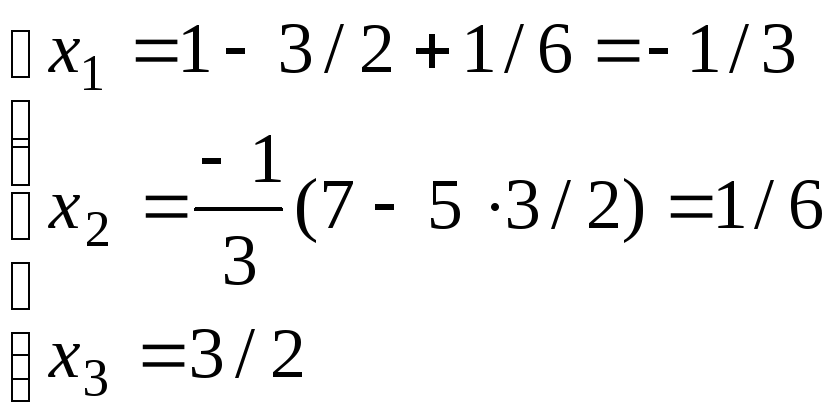.Cвободных неизвестных нет, поэтому решение единственно.

Ответ: (–1/3, 1/6, 3/2).

Задача 4.Решить следующую систему уравнений в зависимости от параметра: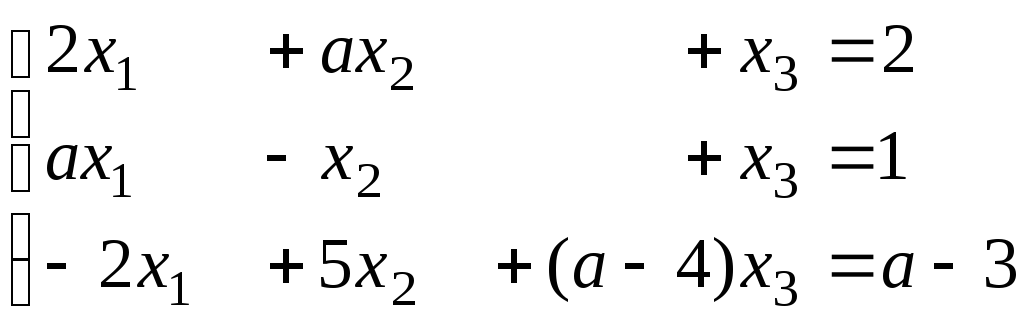

Решение.Выпишем расширенную матрицу системы и приведем её к ступенчатому виду.

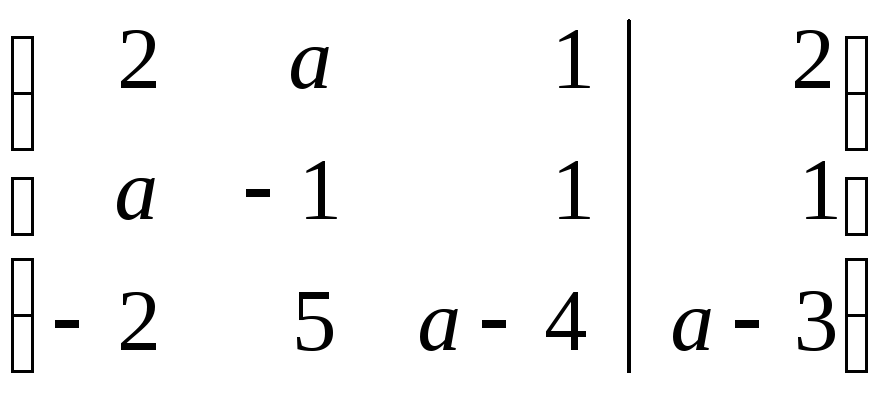
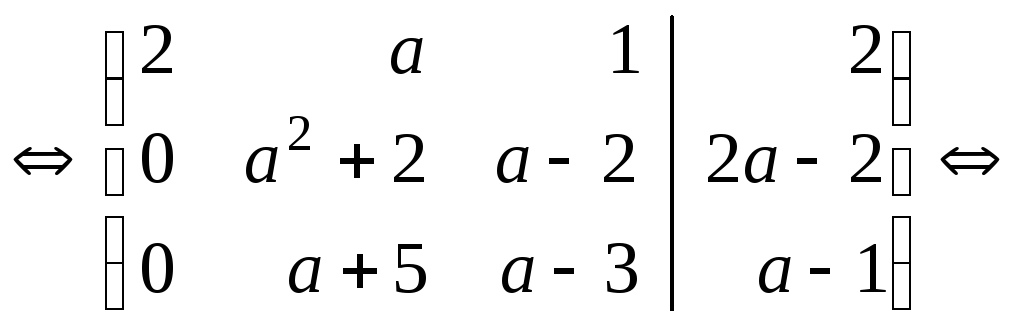
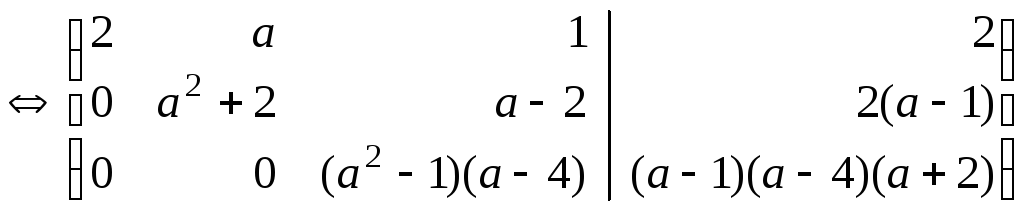
При а=–1 последняя строка матрицы соответствует уравнению 0=1, которое не имеет решений. Следовательно, приа=–1 система не имеет реше­ний.

П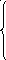риа=1 матрица имеет вид:,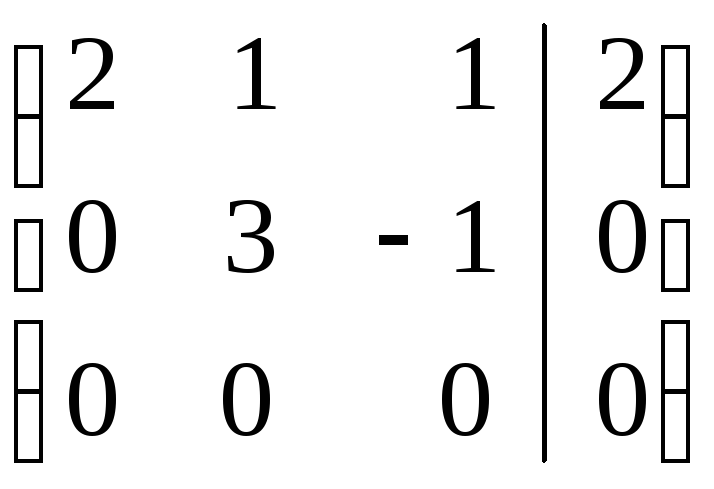

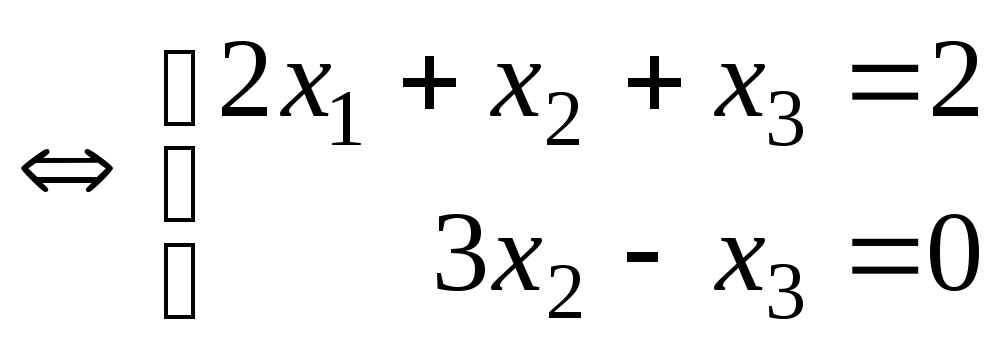П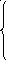ри а=4 матрица имеет вид:, ,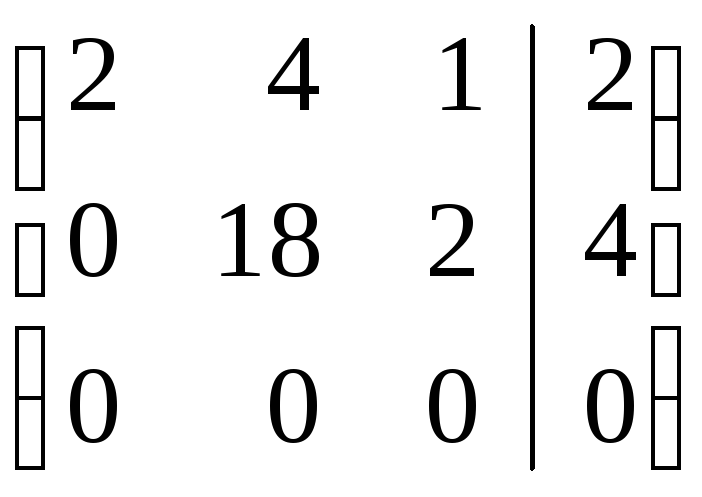

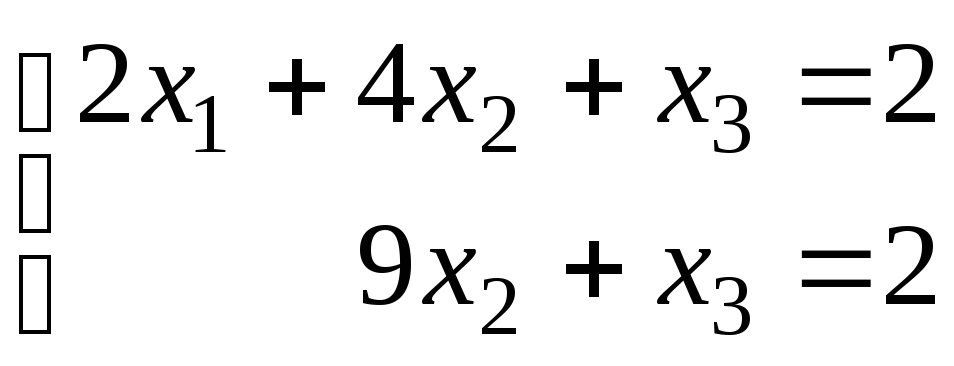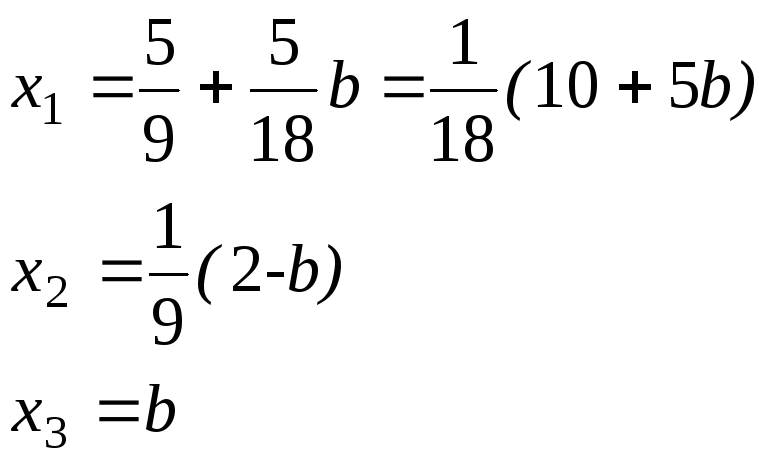
При а, а, аматрица имеет вид:,

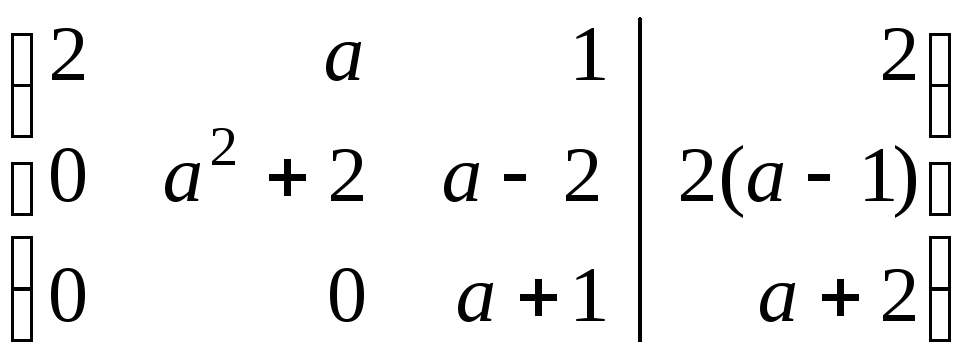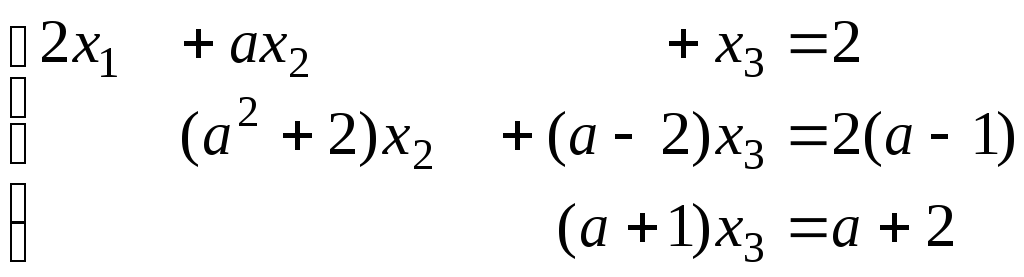
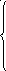
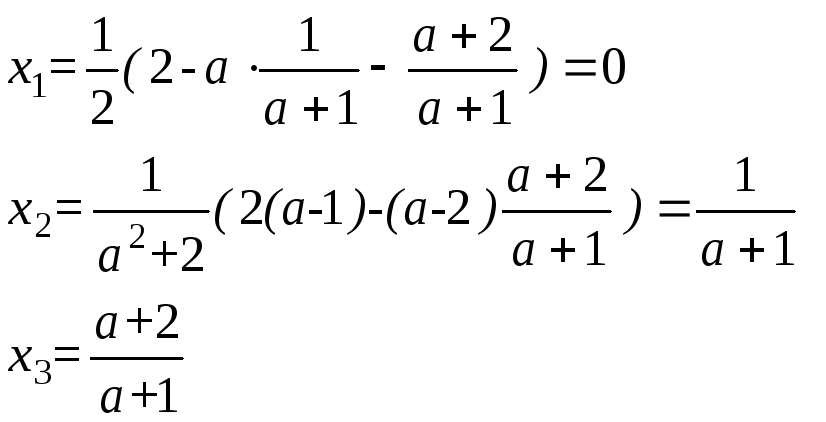
Ответ:

• если а=–1, то система несовместна;

• если а=1, то система совместна неопределенная с реше­нием

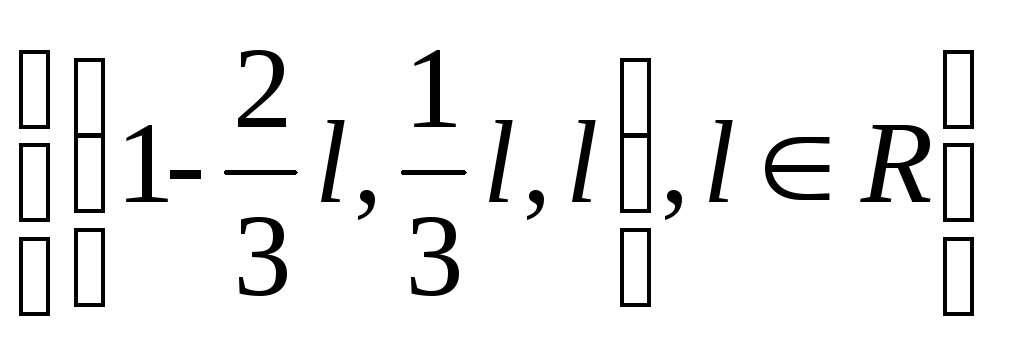
• если а=4, то система совместно неопределенная с решением

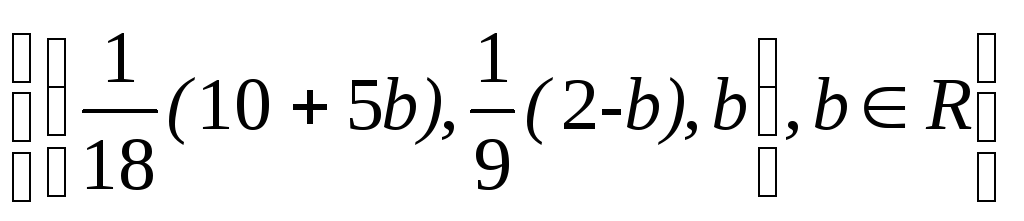
• если ато система совместно определенная с решением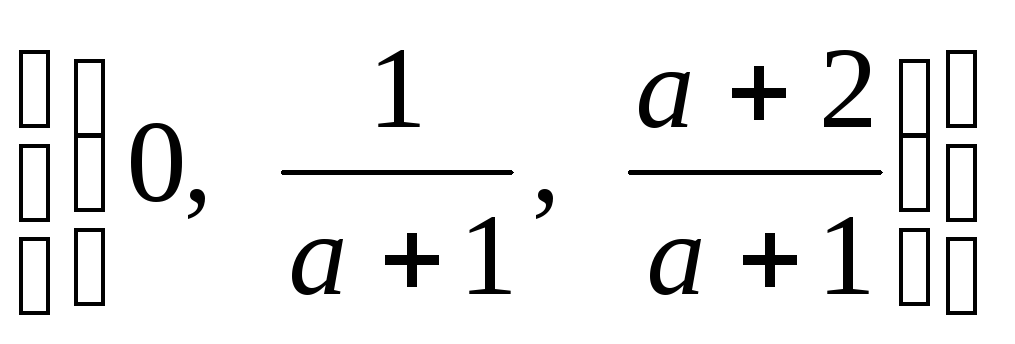

Для самостоятельного решения.

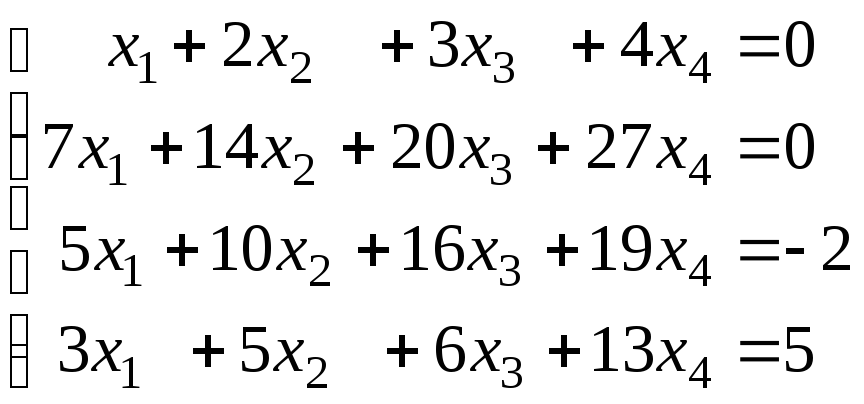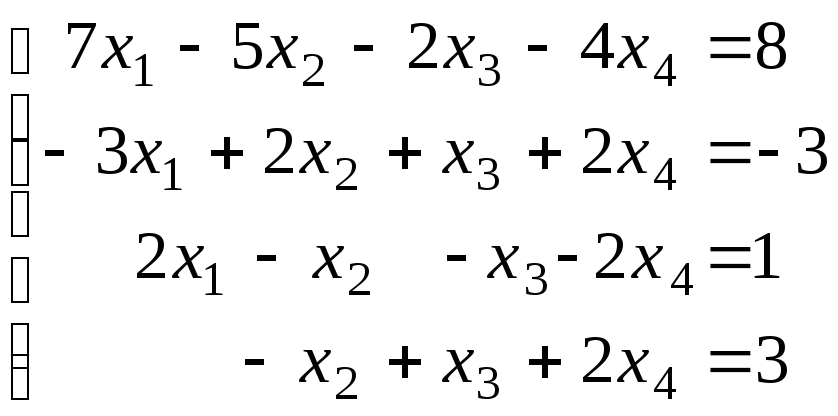1. Решить системы уравнений: а)б)в)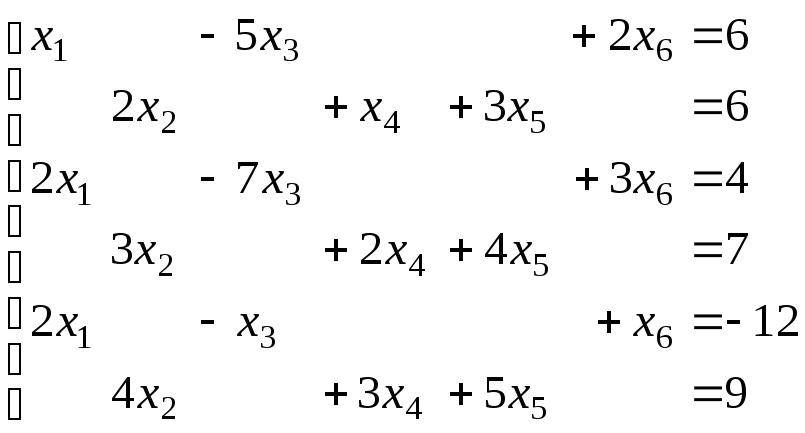

2. Решить при различных значениях параметра системы уравнений:

а)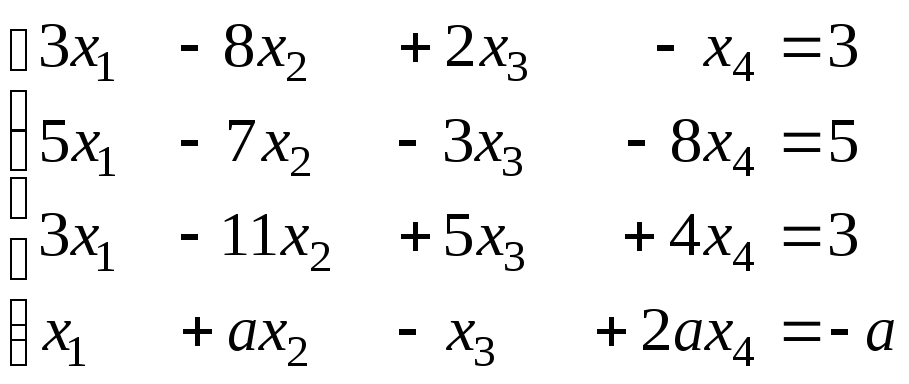б)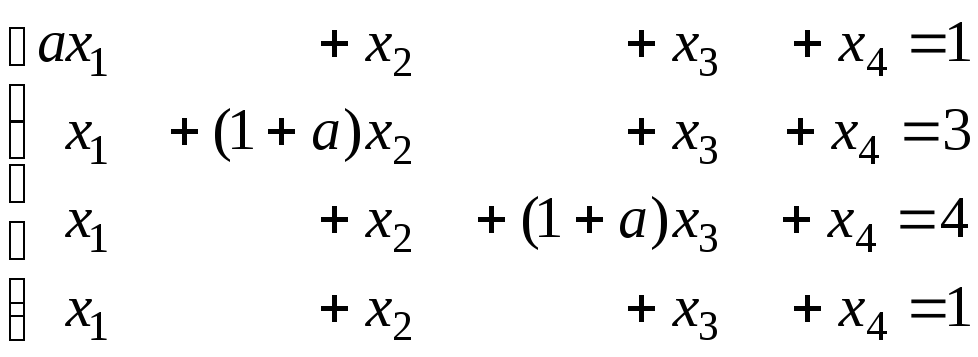.