§3. Однородная система линейных уравнений. Фундаментальный набор решений.

Общий вид О.С.Л.У. Нулевые и ненулевые решения О.С.Л.У. Доста­точное условие существования ненулевых решений. Определение фундамен­тального набора решений О.C.Л.У. Число решений, составляю­щих этот набор. План отыскания какого–нибудь ф.н.

Линейное уравнение называетсяоднородным,если его свобод­ный член равен нулю. Система, состоящая из однородных уравнений, сама на­зывается однородной.Общий вид однородной системыmуравнений сnнеизвестными есть:а₁₁x₁+а₁₂x₂+…+а_1nx_n=0 а₂₁x₁+а₂₂x₂+…+а_2nx_n=0 (1) ………………………… а_m1x₁+а_m2 x₂+…+а_mnx_n=0

Однородная система всегда совместна, так как x₁=0,x₂=0,…,x_n=0 одно из решений системы (1) называемоенулевым решением.

Во многих случаях важно знать, имеет ли данная однородная сис­тема еще и ненулевыерешения.

Теорема 1. Однородная система, в которой число уравнений меньше числа неизвестных, всегда имеет ненулевые решения.

Теорема 2. Однородная система линейных уравнений имеет нену­левые решения тогда и только тогда, когда ранг матрицы, составленной из коэф­фициентов при неизвестных, меньше числа неизвестных.

Свойства решений однородной системы.

1. Если– решение системы (1),тоk(гдеk– любое число) яв­ляется решением системы (1).

2.Еслии– два решения системы (1), то+является ре­шением системы (1).

Теорема 3.Любая линейная комбинация решений однородной сис­темы есть снова решение этой системы .

Рассмотрим множество всех решений однородной системы (1). Это не­которое множество в n-мерном векторном пространствеV_n. Любой базис этого множества называетсяфундаментальным набором решений системы (1).

Иначе говоря, фундаментальный набор – это набор из конечного числа решений:

₁,₂,…_,_p(2) системы (1), удовлетворяющих условиям:

1. Вектора системы (2) линейно независимы;

2. Любое решение является линейной комбинацией векторов сис­темы (2).

Любые два фундаментальных набора состоят из одного и того же числа решений.

Теорема 4. Если₁,₂,…,_pкакой-либо фундаментальный набор реше­ний, то вектор=k₁₁+…+k_p_pпри всевозможных значениях парамет­ровk_1,k_2,…,k_pпробегает все решения системы (1) и поэтому является её общим ре­шением .

Рассмотрим способ построения фундаментального набора ре­шений. Для построения фундаментального набора воспользуемся методом Гаусса.

Применив его к системе (1), после ряда элементарных преобразо­ва­ний, прийдем к равносильной ей системе

с₁₁x₁+ с₁₂x₂+…+с_1,rx_r+с_1,r+1x_r+1+…+с_1nx_n=0 с₂₂x₂+…+с_2,rx_r+с_2,r+1x_r+1+… +с_2nx_n=0 (3) ……………………………………………. c_r,rx_r+с_r,r+1x_r+1+… +с_rnx_n=0

или же к системе, получающейся из этой изменением нумерации неиз­вест­ных. Для определенности допустим, что получилась именно система (3). При­дадим свободным неизвестным в системе (3) следующие значения: x_r+1=1,x_r+2=0,x_r+3=0 ,…,x_n=0, после чего, найдем из системы значения остальных неизвестныхx₁,x₂,…,x_r. Мы получим некоторое решение исходной системы (1) – обо­значим его_r+1 (индекс_r+1 выбран в связи с тем, что при образовании этого решения неиз­вестноеx_r+1играет особую роль). Аналогичным обра­зом, полагаяx_r+1=0,x_r+2=1,x_r+3=0,…,x_n=0 и находя соответствующие значенияx₁,x₂,…,x_r, получим еще одно реше­ние; обозначим его_r+2. И так далее. Всего получим, таким образом,n–rреше­ний системы (1)_r+1, _r+2,...,_n:

_r+1=(l_r+1,1,l_r+1,2,…,l_r+1,r,1,0,0,…,0)_r+2=(l_r+2,1,l_r+2,2,…,l_r+2,r,0,1,0,…,0)_r+3=(l_r+3,1,l_r+3,2,…,l_r+3,r,0,0,1,…,0) (4) ……………………………_n=(l_n1, l_n2,…,l_nr, 0,0,0,…,1)

Векторы _r+1,_r+2,…,_nобразуют фундаментальный набор реше­ний.

Необходимо обратить внимание на следующий факт: число ре­шений в фундаментальном наборе равно n–r, т.e. разности между чис­лом неиз­вестных и рангом матрицыА, составленной из коэффициентов при неизвест­ных.

Задача 1. Найти какой-нибудь фундаментальный набор решений. Запи­сать на его основе все решения системы уравнений:

а) x₁+2x₂+4x₃ –3x₄ =0б)2x₁+3x₂ –2x₃ –5x₄ +x₅=03x₁+5x₂+6x₃ –4x₄ =04x₁+2x₂ +x₃ +2x₄ –3x₅=04x₁+5x₂ –2x₃ +3x₄ =0 –4x₂ +5x₃+12x₄–5x₅=0 3x₁+8x₂+24x₃–19x₄=0–6x₁ –x₂ –4x₃ –9x₄+7x₅=0

Решение. Рассматривая данные системы, как обычные системы ли­нейных уравнений, находим их решения. При этом выясняем наличие фун­даментального набора решений (ранг матрицы системы); определяем число решений, входящих в фундаментальный набор.

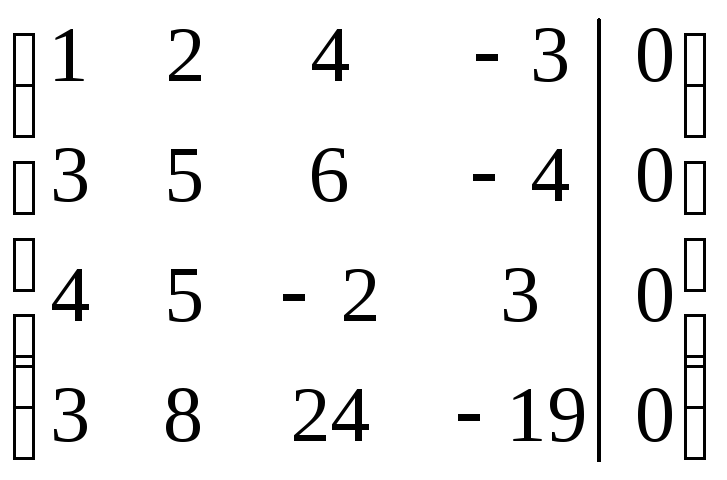
а) Применяем метод Гаусса: Из последней матрицыr_A=2. Так как число неизвестных больше ранга мат­рицы, то исходная система имеет фундаментальный набор решений, состоя­щий изn–r=4–2=2 решений. Из последней системы выразим глав­ные неиз­вестные через свободные:

x₁=–2x₂–4x₃+3x₄ x₁=8x₃–7x₄

x₂= –6x₃+5x₄ x₂=–6x₃+5x₄

Тогда фундаментальный набор, состоящий из двух решений, может быть выбран следующим образом:

Xx1	xx2	xx3	xx4
88	-–6	11	00
––7	55	00	11

Общее решение данной системы можно записать:

=k₁₁+k₂₂, где₁=(8,–6,1,0);₂=(–7,5,0,1);k₁,k₂– произвольные числа.

б) Решаем систему методом Гаусса: ,r_A=2.

И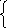з последней системы выразим главные неизвестные через сво­бод­ные:2x₁=–3x₂+2x₃+5x₄–x₅ x₁=–7/8x₃–2x₄+11/8x₅ x₂=5/4x₃+3x₄–5/4x₅ , x₂=5/4x₃+3x₄–5/4x₅.

Фундаментальный набор состоит из n–r=5–2=3 решений и может быть выбран следующим образом:

x1	x2	X3	x4	x5
–7	10	8	0	0
–2	3	0	1	0
11	–10	0	0	8

Общее решение системы можно записать:

=l₁₁+l₂₂+l₃₃, где₁=(–7,10,8,0,0);₂=(–2,3,0,1,0);₃=(11,­–10,0,0,8);l₁,l₂,l₃–произвольные числа.Ответ:

a)₁=(8,–6,1,0);₂=(–7,5,0,1) – фундаментальный набор;=k₁₁+k₂₂(k₁,k₂—произвольные числа) – все решения системы уравнений.

б) ₁=(–7,10,8,0,0);₂=(–2,3,0,1,0);₃=(11,–10,0,0,8) – фундаментальный набор;=l₁₁+l₂₂+l₃₃(l_1,l₂,l₃произвольные числа) – все решения системы уравнений.

Замечание. Всем свободным неизвестным можно придавать про­из­вольные значения. Но чтобы получить фундаментальный набор реше­ний надо заботиться о том, чтобы число частных решений былоn–r(n–число не­известных системы,r–ранг матрицы системы), и чтобы эти решения были ли­нейно независимы.

З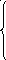адача 2.Проверить образуют ли₁=(2,2,0,4,1) и₂=(–1,0,2,–3,–2) фундаментальный набор решений системы уравнений:

3x₁ –2x₂+2x₃ –x₄ +2x₅=0 2x₁ +3x₂ –4x₃–2x₄ –2x₅=0 3x₁+2x₂ –x₃ –3x₄ +2x₅=0 (1) x₁ –5x₂ +6x₃ +x₄+4x₄=0 6x₁ +x₃ –4x₄+4x₄=0

Решение. I способ.План решения: 1) убеждаемся в том, что₁ и₂яв­ляются решениями системы (1); 2) если₁и₂– решения системы (1), то убеждаемся, что система векторов₁и₂линейно независима; 3) вычисляем ранг матрицы системы и оцениваем число решений, вхо­дящих в фундамен­тальный набор (оно должно быть равно 2). Проводим решение согласно этому плану;

1) непосредственно подставляем координаты ₁в каждое уравне­ние системы:

32–22+20–14+21 =6–4–4+2 =0; 22+32–40–24–21 =4+6–8–2 =0; 32+22–10–34+21 =6+4–12+2=0; 12–52+60+14+41=2–10+4+4=0; 62 +10–44+41 =12–16+4 =0.

Cледовательно,₁– решение системы (1). Аналогично убеждаемся, что₂ – решение системы (1).

2) вектора ₁ и₂– не пропорциональны, следовательно, система век­торов₁и₂– линейно независима;

3) вычисляем ранг матрицы системы: ~ ,r_A=3 Тогда число решений фундаментального набораn–r=5–3=2.

Итак, на все пункты плана получили утвердительный ответ. По этому _{1 и} ₂образуют фундаментальный набор решений. Заметим, что если хотя бы на один пункт плана был получен отрицательный ответ, то₁и₂не образовывали бы фундаментального набора решений.

II cпособ. Находим обычным методом исключения неизвестных общее решение системы (1):,r_A=3.

С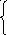вободных неизвестных два (х₄и х₅). Выразим главные неизвест­ные через свободные:x₁=5x₂–6x₃ –x₄ –4x₅; x₁=3/5x₄–2/5x₅; x₂= 2x₃ +2x₅; x₂=4/5x₄–6/5x₅; x₃= 2/5x₄–8/5x₅; x₃=2/5x₄–8/5x₅.

Фундаментальный набор состоит из n–r=5–3=2 решений. Найдём один из них. Положим сначалаx₄=4,x₅=1 (четвертая и пятая координаты век­тора₁), а затемx₄=–3,x₅=–2 (четвертая и пятая координаты вектора₂). Получим частные решения :

x1	X2	x3	x4	x5
2	2	0	4	1
–1	0	2	–3	–2

это и есть вектора ₁и₂.

Таким образом, ₁и₂являются решениями системы (1). Число за­данных решений₁и₂равно числу свободных неизвестных. Нако­нец, убе­ждаемся, что₁и₂линейно независимы. Следовательно,₁и₂составляют фундаментальный набор решений системы (1).

Задача 3.Решить систему линейных уравнений, используя связь ре­шений системы уравнений с решениями соответствующей системой одно­родных уравнений:2x₁+3x₂ –2x₃ –5x₄ +x₅= –1 4x₁+2x₂ +x₃ +2x₄ –3x₅= 6 –4x₂+5x₃+12x₄ –5x₅= 8 –6x₁ –x₂ –4x₃ –9x₄+7x₅=–13

Решение. Замечаем, что если в данной системе заменить свобод­ные члены нулями, т. е. перейти к соответствующей однородной системе, то по­лучиться система из задачи 1. Нам известен ее фундаментальный набор реше­ний, а значит и обще решение:=l₁₁+l₂₂+l₃₃, гдеl₁,l₂,l₃произвольные числа и₁=(–7,10,8,0,0);₂=(–2,3,0,1,0);₃=(11,–10,0,0,8).

Так как сумма общего решения соответствующей однородной сис­темы и частного решения данной системы даст выражение для об­щего ре­шения данной системы, то найдем некоторое частное решение данной сис­темы.

Замечаем, что =(1,1,1,1,1) удовлетворяет данной системе. Поэтому=l₁₁+l₂₂+l₃₃+,гдеl₁,l₂,l₃произвольные числа, есть общее решение дан­ной системы. Это же выражение можно расписать покоординатно(–7l₁–2l₂+11l₃+1, 10l₁+3l₂–10l₃+1, 8l₁+1, l₂+1, 8l₃+1)l₁,l₂,l₃R

Ответ:(–7l₁–2l₂+11l₃+1, 10l₁+3l₂–10l₃+1, 8l₁+1, l₂+1, 8l₃+1)l₁,l₂,l₃R

Для самостоятельного решения.

1.Найдите какой-нибудь фундаментальный набор решений соот­ветст­вующей системы однородных уравнений и выразите через него общее реше­ние системы уравнений:

2x₁ –x₂ +3x₃ +x₄ –x₅= 4 x₁ +x₂ –2x₃+2x₄ +x₅= 6 4x₁ +x₂ –x₃+5x₄ +x₅=16 –x₁+5x₂–12x₃+4x₄+5x₅=10

2. Дана система уравнений

4x ₁+x₂ –2x₃ =0 x₁–2x₂ +2x₃+3x₄=0 –5x₁–8x₂+10x₃+9x₄=0 x₁+7x₂ –8x₃–9x₄ =0

и наборы векторов: a) (1,2,3,–1); (2,4,6,–2); б) (1,8,6,1); (3,–12,–12,1); в) (–1,–2,–3,1); (1,14,9,3). Проверьте, какой набор является фундаменталь­ным набором решений данной системы уравнений.