ТЭС_часть2

СПИСОК ВОПРОСОВ:

41.Разложения по системе тригонометрических функции.

42.Разложения сигналов и помех по функциям Уолша.

43.Геометрическое представление сигналов и помех.

44.Проблемы оптимизации систем связи.

45.Оптимизация систем связи «в целом».

46.Оптимизация приемной части систем связи.

47.Преобразование сигналов в системах связи.

48.Амплитудная модуляция.

49.Частотная и фазовая модуляция.

50.Способы формирования сигналов с угловой модуляцией.

51.Импульсная модуляция, импульсная поднесущая.

52.Амплитудно-импульсная модуляция.

53.Широтно-импульсная модуляция.

54.Время-импульсная модуляция.

55.Методы формирования ИМ-сигпалов.

56.Импульсно-кодовая модуляция.

57.Методы уплотнения каналов. Общие принципы уплотнения.

58.Методы частного уплотнения каналов.

59.Временное уплотнение.

60.Общие сведения об оптимальном приеме и фильтрации.

61.Оптимальная фильтрация непрерывных сигналов.

62.Оптимальная фильтрация дискретного сигнала.

63.Оптимальный фильтр при белом шуме.

64.Импульсная переходная функция согласованного фильтра.

65.Оптимальный фильтр как коррелятор.

66.Примеры синтеза согласованных фильтров.

67.Квазиоптимальные фильтры.

68.Методы приема сигнала. Метод однократного отсчета.

69.Обнаружение сигналов с суммированием отсчетов.

70.Интегральный прием.

71.Корреляционный прием.

72.Амплитудная телеграфия. Некогерентный прием.

73.Когерентный прием при амплитудной телефонии.

74.Частотная телеграфия.

75.Фазовая телеграфия.

76.Относительная фазовая телеграфия.

77.Прием сигналов как статистическая задача.

78.Критерий идеального наблюдателя.

79.Критерий минимума среднего риска.

80.Критерий отношения правдоподобия.

81.Понятие об информационном критерии. Минимаксный критерий.

82.Критерий Неймана-Пирсона.

2

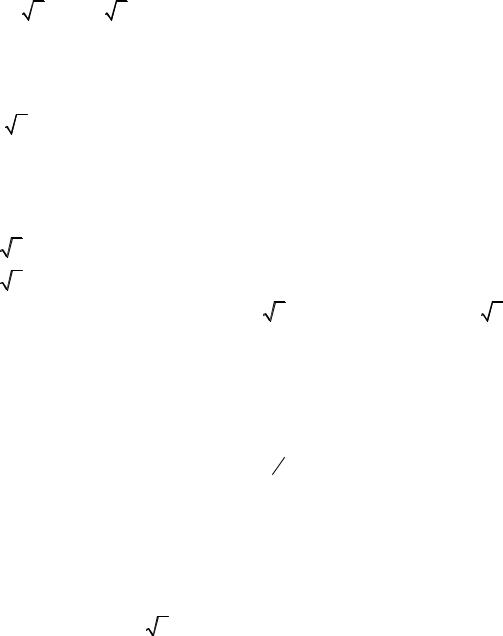
41. Разложения по системе тригонометрических функции.

Рассмотрение тригонометрических функций обусловлено следующим:

1)тригонометрические функции они обладают свойством ортогональности;

2)гармонические колебания не искажаются при прохождении через линейные системы;

3)удобный и простой аппарат;

4)гармонические колебания (функции) легко генерируются, что немаловажно для сотовой связи. Они легко получаются при подаче импульсного сигнала на нелинейный элемент.

Система тригонометрических функций образована из множества функций вида:

Разложение в этом случае будет записано, как:

3

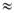
Если представлять непрерывные функции ряда Фурье достаточно учитывать конечное число членов, также как и простом разложении, т.е. необходимо брать не бесконечный ряд, а ограниченный. Мы вводим ограничение по верхним пределам, т.к. ведётся работа с реальными каналами, которые имеют ограниченную полосу частот и, следовательно, в эту полосу попадает ограниченное число гармоник.

Если эта величина будет достаточно большой, то мы можем считать, что:

где n2 и n1 отвечают за количество гармоник на верхней и нижней границе полосы

То есть мы имеем дело с ограниченным полосовым сигналом ∆f = fB − fH .

Если fH = 0 , что часто бывает (например, телевизионный сигнал), тогда число гармоник, которое нам нужно рассматривать будет равно: N = 2 fBT ( ).

Резюме:

Выражение ( ) определяет число степеней свободы колебания со спектром, расположенным в диапазоне [fH , fB ] и получило название полосовое колебание, а выражение ( ) определяет число степеней свободы колебания со спектром [0, fB ],

которое получило название видеоколебание.

При разложении колебания в ряд Котельникова, то N – есть число гармоник, при представлении колебания в частотной области или число гармоник при представлении колебаний в частотной области.

4

42. Разложения сигналов и помех по функциям Уолша.

Особенность функции Уолша в том, что они также как и цифровые сигналы (функции) могут принимать всего два значения +1,−1.

Функции Уолша получаются из боле простых ортогональных функций Радамахера:

Функция Радамахера на интервале [0,T ] разбивается на 2k равных подинтервалов ∆T , в котором функция rk (t ) принимает попеременно знаки +1 и −1, т.е. имеют вид меандра.

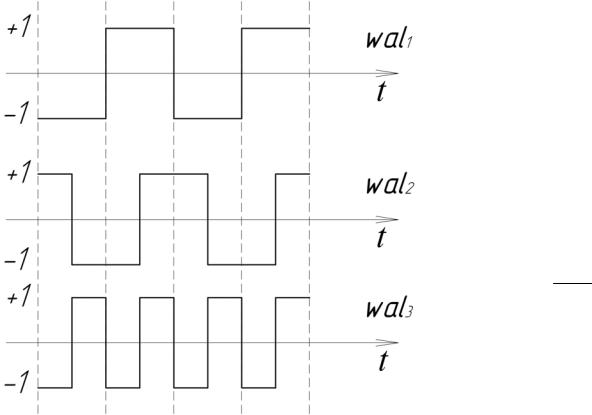
Меандр – импульсная функция с чередующимися знаками +1 или −1. На рисунках показаны функции Радамахера:

первого порядка

второго порядка

третьего порядка.

Рассмотрим, как получаются функции Уолша из функций Радамахера. Функция Уолша нулевого порядка вводится по определению, и она равна 1.

wal0 (t )=1.

Для получения функций порядка выше нулевого порядка вводится следующий алгоритм:

1

1) Число, отвечающее за порядок: k = ∑γi 2i−1 =γm 2m−1 +γm−1 2m−2 +... +γ2 21 +γ1 20 ,

i=m

где m – число разрядов кода необходимых для представления функции Уолша k -го порядка;

γ – весовой коэффициент, имеющий значения 1 или 0 (в зависимости от того, учитывается или нет данный разряд при суммировании).

5

2) Число k , представленное в прямом двоичном натуральном коде перекодируется по правилу: кодовая комбинация натурального кода складывается по модулю два с этой же комбинацией, но сдвинутой на один разряд вправо, при этом младший разряд отбрасывается. Полученный код носит название кода Грея.

Если число в прямом двоичном коде выражается в виде весовых коэффициентов:

γm ,γm−1,...,γ2 ,γ1 ,

то в коде Грея эти коэффициенты можно записать в виде: bm ,bm−1,...,b2 ,b1 .

Но bm =γm , bm−1 =γm γm−1,... , b1 =γ2 γ1 . 3) Запись самой функции Уолша.

Выражение функции Уолша через функцию Радамахера записывается следующему правилу:

m

walk (t )= ∏ ri (t ) bi = r1 (t ) b1 r2 (t ) b2 ... rm (t ) bm .

i=1

Это правило показывает, что функция Уолша получается перемножением функции Радамахера в определенные комбинации, задаваемых коэффициентов bi .

Вид функции Уолша k первого, второго и третьего порядка:

Получаем систему функции Уолша:

{walk (t )}.

Для этой системы характерно расположение функций возрастания числа перемен знака на интервале [0,T ].При этом число перемен знака

функций равно m2 , а для нечётных функций равно m2+1 .

В этой системе также работают модифицированные функции Уолша: {calk (t ), salk (t )} – функция Уолша в ортогональной системе,

{hadk (t )} – функция Уолша-Адамара.

В системе основного применения используют матрицу Адамара. {palk (t )} – функция Уолша-Пейли.

Функции Уолша получили широкое применение в системах связи с уплотнения по частоте, по времени и по коду. Также применяется в системах сотовой связи CDMA.

6

43. Геометрическое представление сигналов и помех.

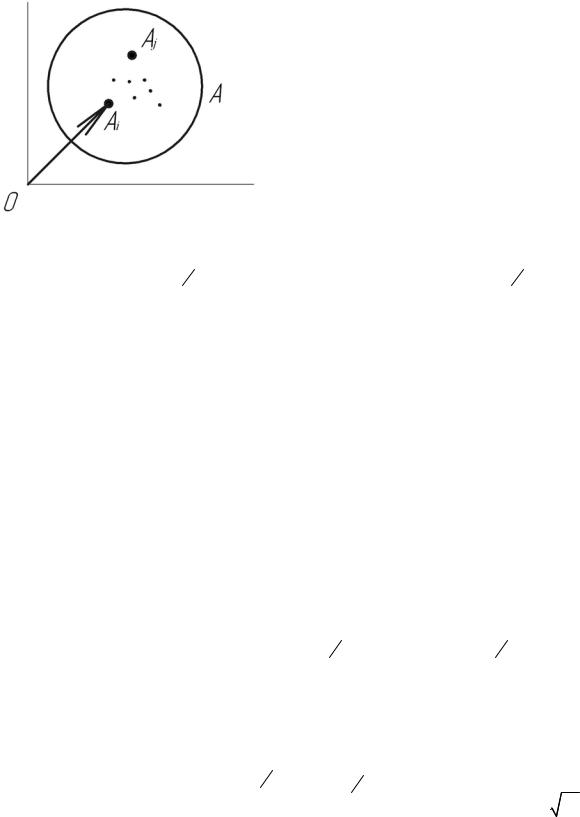
В современной теории передачи сигналов широко используют геометрическое представление сигналов и помех, т.е. представляют их в виде некоторых элементов (точки, векторы).Мы будем представлять сигналы и помехи в многомерном пространстве. Допустим, что некоторые математические объекты Ai (вектора, точки и т.д.) являются

элементами множества A , т.е. Ai A. Если над объектами Ai можно произвести

линейные операции, то множество A принадлежит к линейному пространству, а его элементы Ai соответственно точки этого множества.

Это пространство может иметь любую размерность. В общем случае мы считаем, что множество имеет n – мерную размерность. Если в таком пространстве определено расстояние между двумя точками, то пространство называется метрическим. Расстояние между началом координат и точкой Ai называется

нормой, тогда пространство будет называться нормированным.

Определение: Линейное метрическое нормированное пространство, в котором определены норма и расстояние в следующем виде:

называется Евклидовым пространством.

Если n → ∞, то мы имеем гильбертово пространство.

Мы будем задавать наш сигнал и помехи в Евклидовом пространстве. Ai – вектор, длина которого есть норма.

Для определения длины или модуля этих векторов воспользуемся соотношениями:

Так как базисные функции обладают свойством ортогональности и при этом являются ортонормальными (Q =1). В этом случае длина векторов и норма будут соответствовать

одной и той же величине, т.е.:

7

где ua φ – мгновенное эффективное значение равное корню квадратному из мощности, причём мощностьJJGдолжна быть активная.

Аналогично для ub :

Резюме:

Таким образом, длина вектора в n – мерном пространстве определяется эффективным значением соответствующего колебания тока или напряжения (в зависимости оттого, что мы примем за исходное колебание).

Посмотрим, какой физический смысл несёт расстояние между векторами:

Это расстояние определяет степень различия между двумя колебаниями, чем меньше эта

Этому выражению соответствует среднее значение произведения колебаний, т.е.:

ua ub = T∫ua (t )ub (t )dt ( ) – это выражение характеризует эффективное

0

взаимодействие между колебаниями ua (t ) от ub (t ).

Можно ввести понятие взаимной мощности колебания ( Pab ). Легко убедиться, что с

8

При геометрическом представлении кодированных сигналов широко используется n – мерное пространство с неевклидовой метрикой, в котором расстояние между векторами определяется по правилу:

n

α (x, y)= ∑(xi − yi ),

i=1

где n – число элементов комбинации данного кода (значность кода),

xi , yi – значность соответствующих разрядов кодовых комбинаций (по сути это

координаты векторов в евклидовом представлении)

Геометрической моделью n – значного двоичного кода является n – мерный куб с ребром равным "1".

Каждая из 2n – вершин которого представляет одну из возможных комбинаций. Возьмём трёхзначный код, т.е. 23 =8 . Значит, мы имеем 8 кодовых комбинаций.

Вектор (каждая комбинация данного кода) имеет три координаты. Расстояние в пространстве ln равно

числу разрядов, которых этих комбинации отличаются друг от друга.

Найдём расстояние между 001 и 010. Воспользуемся правилом и получим:

α = 0 −0 + 0 −1 + 1−0 = 2

Мы видим отличие по двум разрядам, т.е. в кубе мы должны пройти два

ребра. Таким образом, число рёбер определяет разницу между кодовыми комбинациями.

9

44. Проблемы оптимизации систем передачи информации.

Вклад в теорию оптимизации систем передачи информации внесли В. Котельников и К. Шеннон. Котельникова и Шеннона объединяет статистический подход к решению проблем передачи сообщений, т.е. можно использовать статистическую теорию передачи информации, а основной задачей этой теории является решение проблемы оптимизации систем передачи информации.

В любой системе передачи информации степень соответствия принятого сообщения с переданным (достоверность) определяется тремя факторами:

1)наличие помех;

2)неидеальность и нестабильность характеристик систем передачи информации;

3)неидеальность среды;

Если критерии оценки качества системы передачи информации выбраны, то её показатели будут тем выше, чем лучше выбраны способы формирования сигнала с учётом указанных трёх факторов. Таким образом, можно представить такую идеальную систему, показатели качества которой окажутся самыми высокими. Такая система передачи информации будет оптимальна с точки зрения выбранных критериев.

При оптимизации нужно получить ответ на следующие вопросы:

1)Какова структура оптимальной системы передачи информации?

2)Как оценить качество работы оптимальной системы передачи информации?

3)Как выбрать параметры оптимальной системы передачи информации?

4)Как реализовать оптимальной системы передачи информации?

5)Каковы методы приближения реальных системы передачи информации к оптимальным системам передачи информации?

К сожаления получить ответы на все поставленные вопросы не удаётся, даже используя “большую” теорию Котельникова и Шеннона не удается, т.к.:

1)возникают математические трудности и проблемы формализации задачи, как единой;

2)отсутствует разработанный метод оптимизации сложных систем.

Так как телекоммуникационная система относится к классу сложных систем, поэтому для решения задач оптимизации приходиться упрощать модели системы и вводить ряд дополнительных ограничений.

В мировой практике и теории сложилось два направления развития оптимизации систем передачи информации:

1)оптимизация систем передачи информации «в целом»;

2)оптимизация приёмной части, которая сводится к способу формирования приёмника при выбранном сигнале, структуре передачи и т.д.

Таким образом, оптимизация – это выбор “наилучшей” структуры или “наилучших” правил при заданных критериях качества и при заданных исходных данных.

10