6 Ротор векторного поля. Формула стокса

Если векторное поле 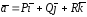имеет дифференцируемые в точке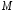составляющие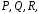торотором (или вихрем) векторного поля 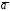в точке 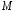называется вектор

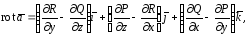
где частные производные вычислены в этой точке.

В символической форме имеет вид:

. (14)

Векторное поле 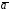называетсябезвихревым в области , если в каждой ее точке

Если 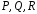дифференцируемы в области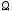и в этой области расположен некоторый замкнутый контур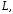то для любой незамкнутой поверхности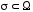, опирающейся на контур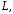имеет местоформула Стокса.

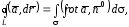(15)

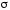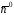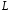где на берется та сторона, в точках которой вектор нормалинаправлен так, чтобы видимый с его конца обход контурасовершался против часовой стрелки (ориентация поверхности согласована с обходом контура).

Формула Стокса позволяет свести вычисление циркуляции векторного поля 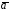по контуру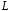к вычислению потока полячерез незамкнутую поверхность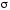, опирающуюся на контур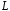(- граница незамкнутой поверхности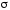). Заметим, что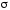- любая поверхность, имеющая границей контур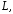поэтому возможен наиболее простой ее выбор.

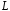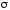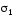Если через контур провести две поверхностиито

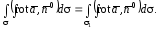
Учитывая, что 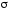и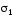ограничивают некоторую пространственную область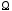и меняя направление нормали на поверхностина противоположное т.е. на внешнее по отношению к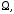получим

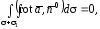
т. е. поток вихря через замкнутую поверхность равен 0. Это означает, что поле вихря является соленоидальным.

Для плоского векторного поля 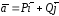формула Стокса принимает частный вид

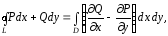(16)

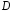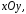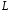где - замкнутая область на плоскостиа- граница этой области с положительным направлением обхода. Формула (16) называетсяформулой Грина.

Задача 7. Вычислить с помощью формулы Стокса циркуляцию поля вектора 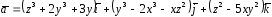по контуру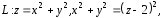положительно ориентированному по отношению к оси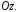

Решение. Построим контур 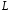(рисунок 6). Этот контур - окружность радиусом 1 в пересечении параболоида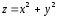и конуса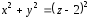

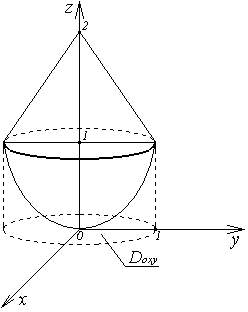
Рисунок 6

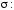
Простейшей поверхностью, опирающейся на этот контур, является плоскость 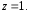Заданная ориентация означает, что с конца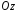обход виден совершаемым против часовой стрелки. Тогда нормалью к плоскости является вектор.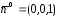

Вычислим по формуле (14)

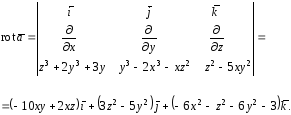
Вычисляем циркуляцию по формулам (15) и (16)

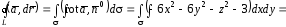
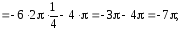
где 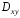- проекция круга радиусом 1 на плоскость.

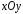7 Потенциальное векторное поле. Вычисление линейного интеграла в потенциальном поле

Векторное поле 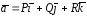, заданное в области, называетсяпотенциальным, если в области 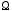существует такая скалярная функция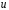, что вектор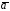можно представить в виде градиента этой функции:

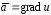. (17)

Функция 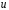называется потенциальной функцией илипотенциалом векторного поля. Из формулы (3.17) следует , что

и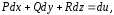

т. е. 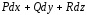- есть полный дифференциал потенциала этого поля.Критерием потенциальности векторного поля служит равенство

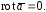(18)

Следовательно, для того чтобы векторное поле было потенциальным необходимо и достаточно, чтобы оно было безвихревым.

Выполнение условия (18) в области 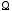приводит не только к потенциальности векторного поля, но и к следующим результатам:

а) в области 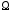существует потенциал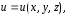который может быть определен с точностью до постоянной по формуле

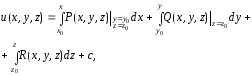(19)

где 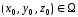- любая фиксированная точка;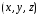- переменная точка в области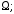- произвольная постоянная. Во втором интеграле формулы (19) постоянно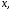а в третьем -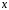и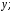

б) циркуляция векторного поля по любому замкнутому контуру 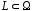равна нулю:

Если же хотя бы в одной точке, внутренней по отношению к контуру 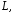поле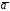не определено, циркуляция по этому контуру может и не обратиться в нуль, хотя поле потенциально;

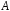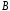в) для любых двух точек иобласти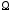значение линейного интеграла векторного поля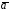

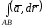
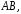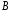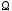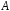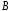не зависит от формы кривой соединяющей точкиии расположенной в, а зависит только от положения точекив области;

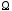г) линейный интеграл этого поля вдоль любого контура 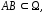соединяющего точкии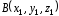равен разности значений потенциала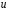в конечной и начальной точках контура:

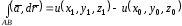. (20)

Физический смысл этого результата: если 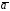- силовое поле, то разность потенциалов между точкам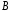ии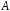равна работе, которую поле совершает при перемещении материальной точки изв.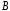

Задача 8. Доказать, что поле вектора

является потенциальным. Найти его потенциал и вычислить линейный интеграл поля 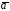от точки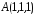до точки.

Решение. Так как поле определено и дифференцируемо в любой точке пространства 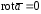и (проверьте самостоятельно), то данное поле потенциально. Найдем потенциал поля по формуле (19), взяв в качестве точки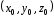начало координат:

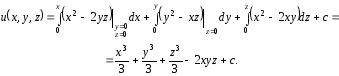
Линейный интеграл вычислим по формуле (20)