
- •Теория поля
- •Составители: елисеев Игорь Спартакович
- •Содержание
- •1 Скалярное поле. Производная по направлению и градиент
- •2 Векторное поле. Векторные линии
- •3 Поток векторного поля
- •4 Формула остроградского. Дивергенция векторного поля
- •5 Линейный интеграл и циркуляция векторного поля
- •6 Ротор векторного поля. Формула стокса
- •7 Потенциальное векторное поле. Вычисление линейного интеграла в потенциальном поле
- •8. Варианты заданий
МИНИСТЕРСВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Уфимский государственный авиационный технический университет
Кафедра математики
Теория поля
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к решению задач и выполнению
расчетно-графической работы по дисциплине «Математика»
для студентов-заочников всех специальностей и направлений
Уфа 2004
УДК 517.3
Составители: Елисеев И.С., Сафиуллина Ф.Г., Сысоев С.Е.,
Халфина Э.Х.
Теория поля: Методические указания к решению задач и выполнению расчетно-графической работы по дисциплине «Математика» для студентов-заочников всех специальностей и направлений /Сост. И.С. Елисеев, Ф.Г. Сафиуллина, С.Е. Сысоев, Э.Х. Халфина. /Уфимск. гос. авиац. техн. ун-т. Уфа, 2004, 35 с.
Рассматриваются основные понятия, положения и приложения математической теории поля, что способствует развитию у студентов кругозора в области геометрических представлений, связанных с теорией поля, уяснению тесной взаимосвязи между физическими объектами теории поля и соответствующими математическими понятиями и структурами, относящимися к определенным, кратным и криволинейным интегралам и дифференциальным уравнениям.
Применение теоретических положений и математического описания физических объектов разъясняется на примерах различной степени сложности, что способствует формированию умений и навыков в приложении математической теории для решения практических физических задач.
Предназначены для студентов и лиц, занимающихся самообразованием, изучающих спецглавы математики, включающие математическую теорию поля.
В методические указания включены 30 вариантов индивидуальных заданий.
Ил. 6. Библиогр.: 4 наимен.
Рецензенты: доцент А.В. Рабчук;
доцент Л.М. Никульшина.
Составители: елисеев Игорь Спартакович
САФИУЛЛИНА Фаузия Гатаевна
СЫСОЕВ Сергей Егорович
ХАЛФИНА Элеонора Хамзинична
Содержание
1. Скалярное поле. Производная по направлению и градиент 4
2. Векторное поле. Векторные линии 6
3. Поток векторного поля 8
4. Формула Остроградского. Дивергенция векторного поля 11
5. Линейный интеграл и циркуляция векторного поля 15
6. Ротор векторного поля. Формула Стокса 17
7. Потенциальное векторное поле. Вычисление линейного
интеграла в потенциальном поле 20
8. Варианты заданий 23
Список литературы 35
1 Скалярное поле. Производная по направлению и градиент
Пространственная
область
 ,
в каждой точке
,
в каждой точке которой задано определенное число
(скаляр)
которой задано определенное число
(скаляр) называетсяскалярным
полем.
Скалярное поле задается скалярной
функцией
называетсяскалярным
полем.
Скалярное поле задается скалярной
функцией
 ,
,
определенной
в области
 .
Если поле задано функцией двух переменных
.
Если поле задано функцией двух переменных
 ,
,
то оно называется плоским. Скалярными являются поле температур, поле давлений, поле плотности вещества и др.
Геометрической характеристикой скалярного поля служат поверхности уровня - множества точек пространства, в которых функция принимает постоянное значение.

-
уравнение различных поверхностей уровня
при различных
 .
.
В плоском поле

- уравнение линий уровня.
Формула
 (1)
(1)
дает
производную
скалярного поля
 в
точке
в
точке по направлению
по направлению
 ,
где
,
где
направление единичного вектора
касательной к заданной линии
направление единичного вектора
касательной к заданной линии
 в точке
в точке .
Производная поля в данной точке
.
Производная поля в данной точке по направлению
по направлению характеризует скорость изменения поля
в этом направлении.
характеризует скорость изменения поля
в этом направлении.
Градиентом
скалярного поля
в точке
 называется вектор
называется вектор
 .
(2)
.
(2)
Между
производной поля
 по направлению
по направлению и его градиентом в точке
и его градиентом в точке существует следующая связь :
существует следующая связь :
 (3)
(3)
где
 –угол
между вектором
–угол
между вектором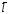 и градиентом в точке
и градиентом в точке .
Из равенства (3) следует, что в каждой
точке
.
Из равенства (3) следует, что в каждой
точке ,
не являющейся критической, градиент
направлен в сторону максимального
возрастания поля
,
не являющейся критической, градиент
направлен в сторону максимального
возрастания поля ,
а модуль градиента равен величине
скорости этого возрастания :
,
а модуль градиента равен величине
скорости этого возрастания :
 .
.
Задача
1. Найти
производную скалярного поля
 в точке
в точке эллипса
эллипса по направлению внешней нормали к эллипсу
в этой точке и градиент поля в этой же
точке.
по направлению внешней нормали к эллипсу
в этой точке и градиент поля в этой же
точке.
Решение.
Направление
 внешней нормали к эллипсу в точке
внешней нормали к эллипсу в точке перпендикулярно к направлению касательной
к эллипсу в этой точке.. Точка
перпендикулярно к направлению касательной
к эллипсу в этой точке.. Точка лежит на части эллипса с уравнением
лежит на части эллипса с уравнением .
Обозначим через
.
Обозначим через – угол, который образует направление
касательной с осью
– угол, который образует направление
касательной с осью .
Тогда
.
Тогда
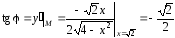 .
.
Если
обозначить угол, образованный направлением
 с осью
с осью ,
через
,
через ,
то из условия перпендикулярности нормали
и касательной получим
,
то из условия перпендикулярности нормали
и касательной получим
 .
.
Находим
направляющие косинусы вектора


Вычислим

и получим по формуле (1)

А
по формуле (2) 
