11.4*. Усиленный закон больших чисел. Закон повторного логарифма.

Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p. Можно ли предвидеть, какова примерно будет относительная частота появлений события A? Положительный ответ на этот вопрос дает теорема Бернулли (1713г.), которая получила название "закона больших чисел" и положила начало теории вероятностей как науке.

Историческая справка. Усиленный закон больших чисел, который впервые был сформулирован и доказан в 1909 г. французским математиком Э. Борелем (1871-1956). Дальнейшее расширение условий приложимости усиленного закона больших чисел было осуществлено Ф. Кинтелли (1917), А.Я. Хинчиным (1927), А.Н. Колмогоровым (1930), Ю.В. Прохоровым (1950).

11.5. Центральная предельная теорема

Термин "центральная предельная теорема" в теории вероятностей означает любое утверждение о том, что при выполнении определенных условий функция распределения суммы индивидуально малых случайных величин стремится к нормальной функции распределения. Исключительная важность центральной предельной теоремы объясняется тем, что она дает теоретическое объяснение следующему многократно подтвержденному практикой наблюдению: если исход случайного эксперимента определяется большим числом случайных факторов, влияние каждого из которых пренебрежимо мало, то такой эксперимент хорошо аппроксимируется нормальным распределением с соответствующим образом подобранными математическим ожиданием и дисперсией.

Рассмотрим простейшие теоремы, относящиеся к центральным предельным теоремам. Пусть {Xn} –последовательность взаимно независимых случайных величин, имеющих конечные математические ожидания M[X_i]=a_iи дисперсии D[X_i]=_i².Введем обозначение .

Теорема Ляпунова. Если для последовательности взаимно независимых случайных величин {X_n} выполняется условие (условие Ляпунова):

,

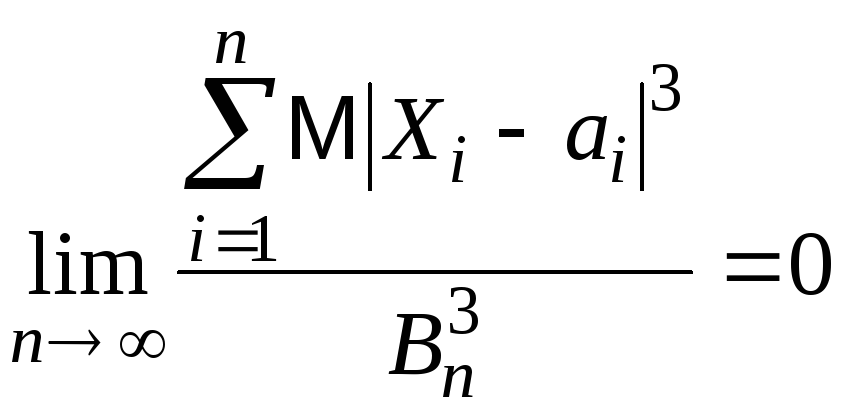то для функции распределения F_n(x) нормированной суммы

имеет место равенство

.

Более простой вид имеет следующая теорема.

Теорема Леви-Линдеберга. Если независимые случайные величины {X_n} имеют одинаковые функции распределения, где M[X_i]=a, D[X_i]=², то функция F_n(x) нормированной суммы:

имеет место равенство

.

Отметим, что интегральная теорема Муавра-Лапласа является центральной предельной теоремой для последовательности независимых одинаково распределенных случайных величин, принимающих два значения: 0 – с вероятностью q и 1 – с вероятностью p (схема Бернулли). Поскольку в этом случае M[X_i]=p, D[X_i]=pq, т.е. выполняются условия теоремы Леви-Линдеберга, то случайная величина 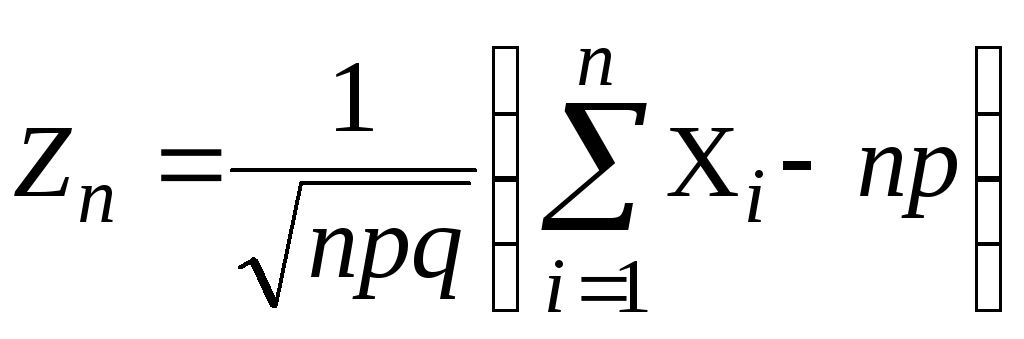имеет стандартное нормальное распределение. Так как – число успехов вn испытаниях Бернулли, то

.

Отсюда получаем формулу Муавра-Лапласа:

.

Историческая справка. Теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определенным предельным значениям, независимо от их закона распределения. Другая группа теорем, относящихся к центральной предельной теореме, устанавливают связь между законом распределения суммы случайных величин и его предельной формой – нормальным распределением. Различные формы центральной предельной теоремы отличаются между собой условиями, накладываемые на сумму составляющих случайных величин. Одна из первых центральных предельных теорем была сформулирована и доказана П. Лапласом (1749-1827) "Аналитическая теория вероятностей" (1812). Один частный случай этой теоремы был известен А. Муавру (1730), в связи с чем эта теорема носит название теоремы Муавра-Лапласа. Существенное продвижение исследований по предельной теореме связано с именем С. Пуассона (1837). Заметим, что как работы Лапласа, так и работы Пуассона и всех последующих исследователей, занимавшихся центральной предельной теоремой, были непосредственно связаны с теорией ошибок измерений. Интерес к нормальному распределению в начале XIX в. возрос в связи с появлением знаменитых исследований Лежандра и Гаусса по формулировке и обоснованию метода наименьших квадратов. Второй толчок, который вызвал дополнительный интерес к предельным теоремам, была статистическая физика, начала которой были построены в середине XIX в. Первый общий результат в этом направлении был сформулирован Чебышевым (1887), но в его доказательстве обнаружились пробелы, восполненные позднее Марковым (1898). Решение вопроса, близкого к окончательному, было получено в 1901 г. А.М. Ляпуновым (1857-1918). Общность результатов Ляпунова произвела огромное впечатление на современников. По-видимому, именно в ту пору и появился термин "центральная предельная теорема". Дальнейшее расширение условий приложимости центральной предельной теоремы было осуществлено Линдебергом (1922), С.Н. Бернштейном (1926), У. Феллером (1935).