11.1. Неравенство Чебышева

Неравенство Маркова. Для любой случайной величины X, имеющей конечное абсолютное математическое ожидание и конечную дисперсию, при любом >0 имеет место неравенство:

(11.1)

Доказательство. Ограничимся ДСВ. Пусть известен закон распределения случайной величины X. По отношению к числу  возможные значения X разбиваются на две группы: одни не превосходят по модулю , а другие – больше . Предположим, что к первой группе относятся первые k значений случайной величины. Математическое ожидание случайной величины |X|:

.

Так как члены этой суммы неотрицательны, то |x_i|p_i0, то отбрасывая первые k слагаемых, получим неравенство:

.

Заменим оставшиеся значения x_i меньшей величиной , от этого неравенство лишь усилится:

.

Отсюда

.

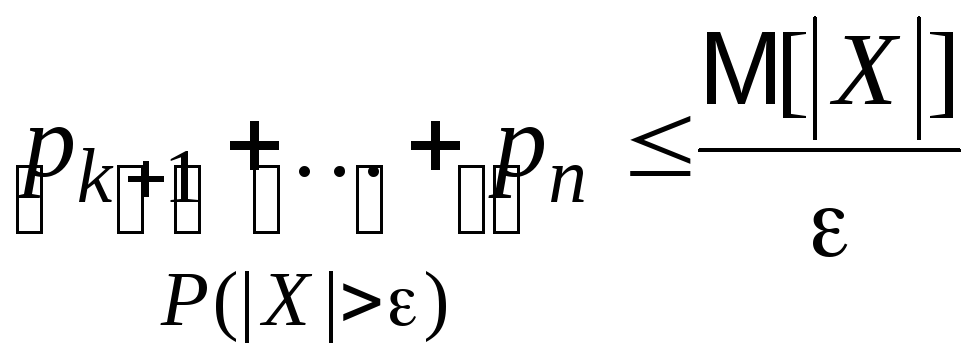Что и требовалось доказать.

Следствие. Для любой случайной величины X, имеющей конечное число абсолютное математическое ожидание и конечную дисперсию, при любой >0 имеет место неравенство:

(11.2)

Действительно, пусть Z=X² – случайная величина, для которой выполняется неравенство X²>². Применяя неравенство Маркова, получим

.

Поскольку

,

то

Что и требовалось доказать.

Пример 11.1. Измеряется скорость ветра в каком-то пункте Земли. Случайная величина X – проекция вектора скорости ветра на фиксированное направление. Оценить вероятность события A={|X|>25 м/с}, если путем многолетних наблюдений установлено, что: а) m=M[X]=5 м/с; б) =1 м/с.

Решение. а) Воспользуемся неравенством

.

б) Воспользуемся следствием из неравенства Маркова

.

Неравенство Чебышева. Для любой случайной величины X, имеющей конечную дисперсию, при любом >0 имеет место неравенство:

. (11.3)

Действительно, применим следствие из неравенства Маркова для случайной величины |X–m|. Тогда

.

Поскольку события |X–m|> и |X–m| противоположны, то

.

Отсюда следует неравенство Чебышева.

Отметим, что неравенство Чебышева справедливо для любых распределений случайной величины X. Оно ограничивает вероятность того, что случайная величина отклонится от своего математического ожидания на величину, более чем на . Из неравенства Чебышева следует, что при уменьшении дисперсии значения случайной величины с большей вероятностью сосредоточиваются около ее математического ожидания. Полагая =t, получим

.

В частности,

при t=1 имеем ,

при t=2 имеем ,

при t=3 имеем .

Замечание. Хотя неравенство Чебышева дает зачастую грубую, а иногда и тривиальную (см., что получилось выше при t=1) оценку вероятности, тем не менее значение его огромно. Выводы, получаемые отсюда, имеют фундаментальное теоретическое значение. Отметим также, что для некоторых распределений вместо неравенств можно получит точные равенства (см., например, тему: "Нормальное распределение").

Пример 11.2. Диаметр изготовляемых болтов представляет собой случайную величину, среднее значение (математическое ожидание) которой равно 20 мм. Среднее квадратичное отклонение, характеризующее погрешность изготовления болтов, равно 0,09 мм. Оценить вероятность того, что отклонение диаметра изготовленного болта от его среднего значения не превысит 0,5 мм.

Решение. По условиям задачи имеем m=20 мм, =0,09 мм. Тогда

.

Пример 11.3. Электростанция обслуживает сеть с 12000 лампами городского уличного освещения. Вероятность включения вечером каждой лампы равно 0,9. Оценить вероятность того, что число включенных вечером ламп будет отличаться от своего математического ожидания не более, чем на 100?

Решение. Число включенных ламп есть величина случайная величина X, распределенная по биномиальному закону, где n=12000, p=0,9, q=0,1. Тогда M[X]=np=10800, D[X]=npq=1080. Воспользовавшись неравенством Чебышева, получим

.

Отметим, что в данном случае можно найти точное значение, применив интегральную теорему Муавра-Лапласа:

.