11.2. Теорема Чебышева

Введем новое понятие. Последовательность случайных величина {X_n} сходится по вероятности к числу a, если для любого сколь угодно малого числа >0 вероятность неравенства |X_n–a| с увеличением n стремится к единице:

. (11.4)

Подчеркнем различие между пределом, вводимым в математическом анализе, ипределомпо вероятности. Если последовательностьX_n стремится кa приn в смысле обычного анализа, то начиная с некоторого номераn для всехnN будет неуклонно выполняться неравенство|X_n–a|; если жеX_n стремится кa приn по вероятности, то для отдельных значенийn неравенство может и не выполняться.

Теорема Чебышева. Пусть X₁, X₂, …, X_n – какая-либо последовательность независимых случайных величин и их дисперсии удовлетворяют условию

. (11.5)

Тогда для всех >0:

, (11.6)

где

, .

Другими словами, среднее арифметическое случайных величин при достаточно большом n сколь угодно мало (по вероятности) отклоняется от постоянной величины.

Доказательство. Применим неравенство Чебышева к случайной величине

.

Для этого необходимо найти ее математическое ожидание и дисперсию. В соответствии со свойствами математического ожидания, получим

.

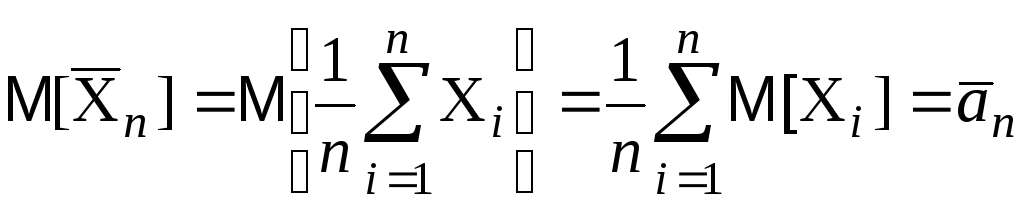В соответствии со свойствами дисперсии, получим

.

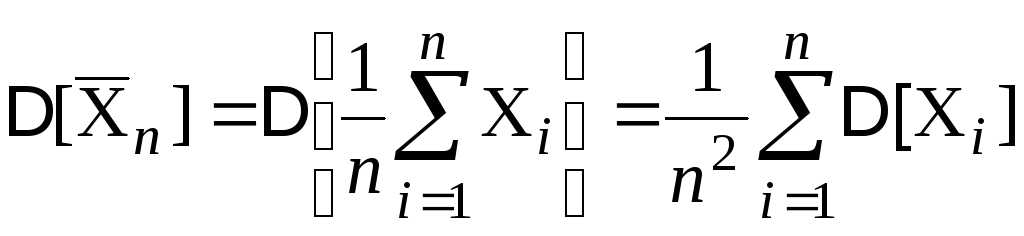Таким образом, неравенство Чебышева для среднего арифметического независимых случайных величин будет иметь вид

, (11.7)

По условию, последнее слагаемое стремится к нулю при n. Поскольку вероятность не может быть больше единицы, то в итоге получается требуемый результат.

Следствие 1. Пусть X₁, X₂, …, X_n – последовательность независимых случайных величин с равномерно ограниченными дисперсиями: D[X_n]<C, то справедлив закон больших чисел (11.6).

Поскольку по условию все дисперсии равномерно ограничены, то неравенство (11.7) можно записать в виде

. (11.8)

Отсюда следует, что при n справедлив закон больших чисел (11.6).

Следствие 2. Пусть X₁, X₂, …, X_n – последовательность независимых случайных величин, имеющие одинаковые математические ожидания (равные a), а дисперсии удовлетворяют условиям теоремы Чебышева, то

. (11.9)

Данное следствие является наиболее простой формой закона больших чисел, применяемой на практике. Например, обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого значения. При каких условиях этот способ измерения можно считать правильным? Теорема Чебышева указывает условия, при которых указанный способ измерения может быть применен: 1) результаты измерений независимы от других измерений; 2) измерения проводятся без систематических ошибок (в этом случае математическое ожидание всех случайных величин одинаковы и равны истинному значению); 3) прибор обеспечивает определенную точность измерений (хотя при этом результаты отдельных измерений различны, но их рассеяние ограничено).

На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого заключается в том, что по сравнительно небольшой случайной выборке судят о всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве зерна судят по небольшой ее пробе. В этом случае число наудачу отобранных зерен мало по сравнению со всей массой зерна, но само по себе его достаточно велико.

Пример 11.4. Для определения средней урожайности поля площадью 1800 га взяли в выборку по 1 м² с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 6 ц. Оценить вероятность того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю не более чем на 0,25 ц.

Решение. Воспользуемся неравенством (11.8), где =0,25,C=0,9, n=1800. Следовательно,

.

Пример 11.5. Определить, сколько надо произвести замеров поперечного сечения деревьев на большом участке, чтобы средний диаметр деревьев отличался от истинного значения a не более чем на 2 см с вероятностью не меньшей 0,95. Среднее квадратичное отклонение поперечного сечения деревьев не превышает 10 см и измерения проводятся без погрешности.

Решение. Будем считать выбор деревьев для замеров таким, что можно считать результаты измерений независимыми случайными величинами. Обозначим через X_iрезультаты измерения поперечного сечения i-го дерева. По условию задачи , следовательноD[X_i]<100.Полагая в неравенстве (11.8) =2,C=100,получим

.

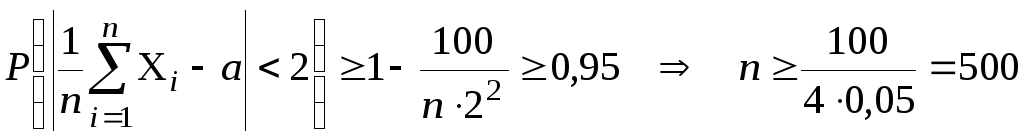Итак, достаточно выполнить 500 замеров поперечного сечения деревьев.

Заметим, что, вообще говоря, существование дисперсии является достаточным, но не является необходимым условием выполнения закона больших чисел. Примером этого может служить теорема Хинчина: для независимых одинаково распределенных X_n (или, как говорят, для независимых наблюдений над одной и той же случайной величиной X) закон больших чисел выполняется в любом случае, когда существует конечное математическое ожидание M[X]. Более того, существуют последовательности независимых одинаково распределенных случайных величин, даже не имеющих математического ожидания, но тем не менее удовлетворяющих закону больших чисел. Отметим, что для сумм независимых случайных величин можно сформулировать более или менее окончательный вид закона больших чисел. В частности, в теореме Колмогорова формулируются необходимые и достаточные условия того, чтобы последовательность взаимно независимых случайных величин подчинялась закону больших чисел.

Пример 11.6*. Последовательность независимых случайных величин X₁, X₂, …, X_n, … задана законом распределения

Xn	–n	0	n
P

Применим ли к заданной последовательности теорема Чебышева?

Решение. Здесь достаточно показать, что для данных независимых случайных величин их дисперсии равномерно ограничены. Вычислим дисперсии

.

Предположим, что n изменяется непрерывно и исследуем на экстремум функцию . Приравняв нулю производную этой функции, найдем критические точкиx₁=0 и x₂=2/ln2. Отбросим первую точку как не представляющую интереса (n не принимает значения, равного нулю). Легко видеть, что в точке x₂=2/ln2 функция (x) имеет максимум. Учитывая, что 2/ln22,9, вычислим дисперсию для ближайших к этому числу целых чисел, т.е. для n=2 и n=3. При n=2 дисперсия D[X₂]=2², при n=3 дисперсия D[X₃]=(9/4)². Очевидно, что (9/4)²>2². Таким образом, наибольшая возможная дисперсия равна (9/4)², т.е. дисперсии случайных величин X_n равномерно ограничены этим числом. Итак, все требования теоремы Чебышева выполняются и, следовательно, к рассматриваемой последовательности эта теорема применима.

Историческая справка. Впервые доказал и сформулировал одну из теорем закона больших чисел швейцарский математик Я. Бернулли (1654-1705). Эта теорема была опубликована в его книге "Искусство предположений" (1713) и является одной из простейших форм закона больших чисел. Теорема Бернулли получила свое первое обобщение лишь в 1837 г. в работе французского математика С. Пуассона (1781-1846): "Исследования о вероятностях суждений". Именно в этом сочинении появился термин "закон больших чисел". Существенный сдвиг в развитии закона больших чисел связан с работой П.Л. Чебышева (1821-1894) "О средних величинах" (1867). В этой работе он перешел от рассмотрения случайных событий к случайным величинам и получил знаменитые неравенства и теоремы, названные впоследствии его именем. Дальнейшие усилия обобщения теоремы Чебышева долго не приносили принципиальных успехов. Лишь в 1907 г. А.А. Марков (1856-1922) нашел условия, обобщающие теорему Чебышева на случай зависимых величин, а 1923 г. А.Я. Хинчин (1894-1959) показал, что если случайные величины не только независимы, но и одинаково распределены, то существование математического ожидания является достаточным условием для применимости закона больших чисел. Принципиальный результат был получен лишь в 1926 г. А.Н. Колмогоровым (1903-1987), который сформулировал о необходимые и достаточные условия для того, чтобы последовательность взаимно независимых случайных величин подчинялась закону больших чисел.

Дальнейшие усилия ученых по углублению содержания закона больших чисел были направлены на получение наиболее общих условий применимости этого закона к последовательности зависимых случайных величин. Для практики исключительно важно выяснить вопрос о применимости закона больших чисел именно к зависимым случайным величинам, т.к. явления в природе и обществе находятся во взаимной зависимости. Впервые соответствующие теоремы были доказаны А.А. Марковым в 1907 г.

Теорема Маркова. Если последовательность случайных величин X₁, X₂, …, X_n такова, что

. (11.10)

то каково бы ни было положительное число  выполняется

, (11.11)

где

, .

Доказательство теоремы Маркова является следствием неравенства Чебышева (докажите самостоятельно). Очевидно, также, что теорема Чебышева является частным случаем теоремы Маркова.

Задача.Покажите, что для последовательности случайных величин (в общем случае, зависимых), рассмотренной в примере 11.6, применима теорема Маркова.

В общем случае, применимость закона больших чисел к суммам зависимых величин в первую очередь связана с неограниченным убыванием зависимости между случайными величинами X_i иX_j при увеличении разности их номеров, т.е.|i–j|. Соответствующие теоремы для случайных величин связанных в цепь также были рассмотрены А.А. Марковым. Основной результат этих работ заключается в том, чтозакон больших чисел приложим к зависимым случайным величинам, если только сильная зависимость существует между случайными величинами с близкими номерами, а с далекими номерами зависимость достаточно слаба. Например, на погоду каждого дня заметно влияет погода предыдущих дней, причем влияние заметно ослабевает с удалением дней друг от друга. Следовательно, многолетняя средняя температура, давление и другие характеристики климата данной местности в соответствии с законом больших чисел практически должны быть близки к своим математическим ожиданиям и являются объективными характеристиками климата местности. Отметим, что более общие условия были рассмотреныС.Н. Бернштейном(1880-1868) в 1946 г.