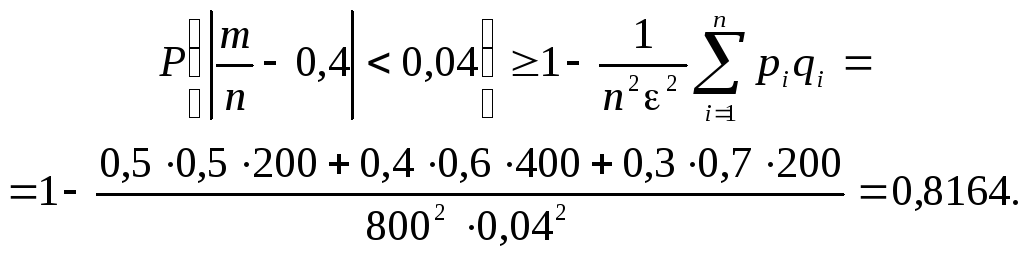11.3. Теорема Бернулли

Пусть производится nнезависимых испытаний, в каждом из которых вероятность появления события Aравна p.Можно ли предвидеть, какова примерно будет относительная частота появлений события A?Положительный ответ на этот вопрос дает теорема Бернулли. Историческая справка. Эта теорема была опубликована Я. Бернулли в 1713 г. Однако доказательство Бернулли было очень сложным. Более простое доказательство теоремы дал П.Л. Чебышев в 1846 г. В 1837 г. С. Пуассон доказал аналогичную теорему в более широких условиях.

Теорема Бернулли. Если в каждом из n независимых испытаний вероятность p появления события A постоянна, то при достаточно большом числе испытаний отклонение относительной частоты от вероятности p будет сколь угодно малым

. (11.12)

Доказательство. Рассмотрим в качестве случайной величины X_i число появлений события A в i-ом испытании. Каждая из этих величин может принимать только два значения: 1 с вероятностью p и 0 – с вероятностью q. Математическое ожидание и дисперсия этих величин равны

, .

Поскольку дисперсии всех этих величин X_i ограничены pq1/4 (доказать самостоятельно) и, кроме того, случайные величины независимы, то применяя к случайной величине неравенство (11.7), получим

.

Поскольку – частота появлений событияA, то получим неравенство Чебышева для относительной частоты появлений событий по схеме Бернулли:

. (11.13)

Отсюда при n получаем утверждение теоремы Бернулли (11.12).

Пример 11.7. При штамповке пластинок из пластмассы брак составляет 3%. Найти вероятность того, что при проверке партии в 1000 пластинок выявится отклонение от установленного процента брака меньше чем на 1%.

Решение. Из условия задачи следует, что n=1000,=0,01,p=0,03,q=1–p=0,97.В соответствии с формулой (11.13), получим

.

Пример 11.8. При каком числе независимых испытаний вероятность выполнения неравенства превысит 0,96, если вероятность появления события в отдельном испытании p=0,7.

Решение. По условию задачи имеем:=0,2,p=0,7,q=0,3.Условие P>0,96равносильно неравенству

.

Следовательно, требуемое неравенство выполняется при числе независимых испытаний, начиная со 132.

Теорема Бернулли устанавливает связь между вероятностью появления события и его относительной частотой появления и позволяет предсказать, какой будет примерно эта частота в nиспытаниях. Из теоремы Бернулли видно, что относительная частота обладает свойством устойчивости при неограниченном росте числа испытаний. В связи с этим на практике вместо вероятности обычно используют относительную частоту (см. тему: "Статистическое определение вероятности"). Отметим, что связь между относительной частотой и вероятность является тем мостом, который связывает теорию вероятностей и математическую статистику.

На практике сравнительно редко вероятность наступления события во всех испытаниях остается одной и той же. Чаще всего она меняется от испытания к испытанию. К схеме испытаний такого типа относится теорема Пуассона.

Теорема Пуассона. Если в последовательности независимых испытаний вероятность появления события A в i-м испытании равна p_i, то

, (11.14)

где – средняя арифметическая вероятность.

Доказательство. Рассмотрим в качестве случайной величины X_i число появлений события A в i-ом испытании. Каждая из этих величин может принимать только два значения: 1 с вероятностью p_i и 0 – с вероятностью q_i. Математическое ожидание и дисперсия этих величин равны

, .

Тогда неравенство Чебышева для относительной частоты появлений событий (11.13) примет вид

. (11.15)

Отсюда при n получаем утверждение теоремы Пуассона (11.14).

Пример 11.9. Проведено 800 независимых испытаний: в 200 из них вероятность появления ожидаемого результата была 0,5, в 400 испытаниях эта вероятность была 0,4, и, наконец, в оставшихся случаях вероятность благоприятствующего исхода была равна 0,3. Оценить вероятность того, что отклонение относительной частоты появления ожидаемого результата от средней вероятности по абсолютной величине не превысит 0,04.

Решение. Найдем среднюю вероятность наступления события в 800 испытаниях:

.

Таким образом, в задаче требуется оценить вероятность

.

Более точная оценка будет иметь следующий вид