113

Лекция 11

Системы случайных величин. Функция распределения двумерной случайной величины. Числовые характеристики двумерной случайной величины. Коэффициент корреляции.

9. Системы случайных величин

9.1. Функция распределения двумерной случайной величины

До сих пор мы рассматривали случайные величины, возможные значения которых определялись одним числом. Такие величины называются одномерными. Например, число очков, которое может выпасть при бросании игральной кости, является случайной величиной; расстояние от орудия до места падения снаряда – непрерывной одномерной случайной величиной. Кроме таких одномерных величин, часто приходится рассматривать одновременно системы из двух, трех и большего числа случайных величин. Например, координаты точки попадания при стрельбе характеризуются двумя случайными величинами: абсциссой и ординатой; осколок, образовавшийся при разрыве снаряда, характеризуется рядом случайных величин: весом, размерами, начальной скоростью, направлением полета и т.д.

При рассмотрении вопросов, связанных с системами случайных величин, удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин {X₁, X₂} можно изобразить случайной точкой на плоскости с координатами X₁ и X₂. Часто вместо образа случайной точки для геометрической интерпретации пользуются образом случайного вектора

.

В дальнейшем мы будем в зависимости от удобства пользоваться как одной, так и другой интерпретацией. Изложение мы проводить в основном для случая двумерных величин. Общий n-мерный случай рассматривается совершенно аналогично.

Функцией распределения F(x, y) двумерной случайной величины {X, Y} называется вероятность совместного выполнения двух неравенств: X<x, Y<y:

. (9.1)

Рис. 9.1

Двумерная функция распределения, по определению, представляет собой не что иное, как вероятность попадания точки с координатами {X, Y} в бесконечный квадрант с вершиной в точке (x,y), лежащий левее и ниже ее (см. рис. 9.1).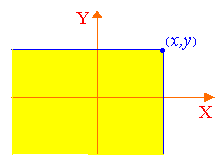

Рассмотрим свойства двумерной функции распределения, которые аналогичны свойствам функции распределения одномерной случайной величины.

Так как F(x,y) – вероятность, то очевидно следующее свойство:

Свойство 1. Функция распределения – величина неотрицательная, не превышающая единицы:

.

Свойство 2. Функция распределения есть неубывающая функция по каждому аргументу:

,

.

Эти неравенства следуют из свойств одномерных функций распределения, которые получаются из F(x,y) при фиксировании y и x соответственно.

Свойство 3. Если хотя бы один из аргументов стремится к –, то функция распределения стремится к нулю:

.

Эти равенства следуют из того, что события {X₁<–} и {X₂<–} есть события невозможные.

Свойство 4. Если оба аргумента стремятся к +, то функция распределения стремится к единице:

.

Это равенство следуют из того, что события {X₁<+} и {X₂<+} есть события достоверные.

Свойство 5. Если один из аргументов обращается в +, то функция распределения F(x,y) становится функцией распределения, соответствующей другому аргументу:

,

.

Первое равенство следуют из того, что события {Y<+} есть событие достоверное, тогда F(x,+) определяет вероятность события {X<x}, т.е. представляет собой функцию распределения составляющей X. Аналогично обосновывается второе равенство.

Зная функцию распределения F(x,y) можно найти вероятность попадания случайной величины {X, Y} в прямоугольник со сторонами R=(x₁X<x₂, y₁Y<y₂):

. (9.2)

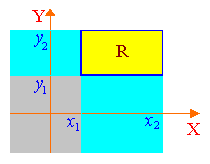Рис. 9.2

Действительно, вероятность попадания в прямоугольникR равна вероятности попадания в квадрант (x₂,y₂) минус вероятность попадания в квадрант (x₁,y₂) минус вероятность попадания в квадрант (x₂,y₁) плюс вероятность попадания в квадрант (x₁,y₁) (так как мы дважды вычли вероятность попадания в этот квадрант).