128

ЛЕКЦИЯ 13

Функции случайных величин. Числовые характеристики функции случайной величины. Законы распределения функции случайной величины. Функции двух случайных величин. Композиция законов распределения.

10. ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН

10.1. Числовые характеристики функции случайной величины

Если каждому возможному значению случайной величины X соответствует одно возможное значение Y, то Y называют функцией случайной величины X и записывают в виде Y=(X).

Если функция (x) однозначная, то каждому возможному значению случайной величины (X) соответствует вполне определенная вероятность, связанная с вероятностью соответствующего возможного значения случайной величины X. Поэтому, если X – дискретная случайная величина, то математическое ожидание величины Y=(X) будет равно

, (10.1)

а дисперсия вычисляется по одной из двух формул:

, (10.2)

Если X – непрерывная случайная величина с плотностью распределения f(x), то

, (10.3)

и

, (10.4)

Пример 10.1. Дискретная случайная величина X описывается следующим законом распределения

X	–1	0	1	2
P	0,2	0,1	0,3	0,4

Найти математическое ожидание и дисперсию случайной величины Y=2^X.

Решение.

M[Y] = 2^–10,2+2⁰0,1+2¹0,3+2²0,4 = 2,4;

D[X] = M[Y²]–M²[Y] = (2^–1)²0,2+(2⁰)²0,1+(2¹)²0,3+(2²)²0,4–2,4²=1,99.

Пример 10.2. Непрерывная случайная величина X описывается плотностью распределения:

Найти математическое ожидание и дисперсию случайной величины Y=X².

Решение.

10.2. Законы распределения функции случайной величины

Во многих задачах практики, особенно в математической статистике, необходимо находить не только числовые характеристики, но и распределения функции случайной величины.

Если X – дискретная случайная величина, описываемая законом распределения

X	x1	x2	…	xn
P	p1	p2	…	pn

и функция (x) – монотонная, то дискретная величина случайной величины Y=(X) описывается следующим законом распределения:

X	(x1)	(x2)	…	(xn)
P	p1	p2	…	pn

Однако, если (x) – немонотонная функция, то среди ее значений (x₁), (x₂), …, (x_i) могут быть равные. В этом случае столбцы с равными значениями (x_i) объединяются в один столбец, а соответствующие вероятности складываются.

Пример 10.3. Дискретная случайная величина X задана законом распределения

X	–3	–2	–1	0	2	4
P	0,2	0,1	0,3	0,1	0,2	0,1

Найти закон распределения случайной величины Y=X²+1.

Решение. Найдем возможные значения случайной величины Y:

Поскольку значению Y=5 соответствует два значения X: x₁=–2 и x₅=2, то вероятность события Y=5 будет равна сумма вероятностей событий X=–2 и X=2: P(Y=5)=0,1+0,2=0,3.

Y	1	2	5	10	17
P	0,1	0,3	0,3	0,2	0,1

Пусть теперь X – непрерывная случайная величина с плотностью распределения f(x) и (x) – монотонно возрастающая функция. Тогда функция распределения G(y) случайной величины Y=(X) будет связана с функцией распределения F(x) случайной величины X следующим образом:

G(y) = P(Y<y) = P[(X)<y] = P[X<(y)] = F[(y)],

где (y)=^–1(y). Дифференцируя последнее равенство по y, получим

.

Поскольку G'(y)=g(y) есть плотность распределения случайной величины Y, а F'(x)=f(x) – случайной величины X, то

g(y) = F'[(y)]'(y).

Если (x) – монотонно убывающая функция, то аналогично получим

g(y) = –F'[(y)]'(y).

Объединяя оба случая, т.е. когда функция (x) является монотонной, получим

. (10.5)

Если функция (x) на интервале возможных значений X не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция (x) монотонна, и найти плотности распределений g_i(y) для каждого из интервалов монотонности, а затем представить g(y) в виде суммы

.

Например, если функция (x) монотонна на двух интервалах, в которых соответствующие обратные функции равны ₁(y) и ₂(y), то

. (10.6)

Пример 10.4. Задана плотность распределения

нормально распределенной случайной величины X. Найти плотность распределения случайной величины Y=X².

Решение. Найдем из уравнения y=x² обратную функцию. Так как в интервале данная функция не монотонна, то разобьем это интервал на участки (–,0) и (0,+), в которых рассматриваемая функция монотонна. На интервале (–,0) обратная функция имеет вид ; на интервале (0,+) обратная функция имеет вид . Найдем производные от этих функций:

, ,

а также

, .

Тогда

.

Так как y=x², причем –<x<+, то 0<y<+. Таким образом, получаем

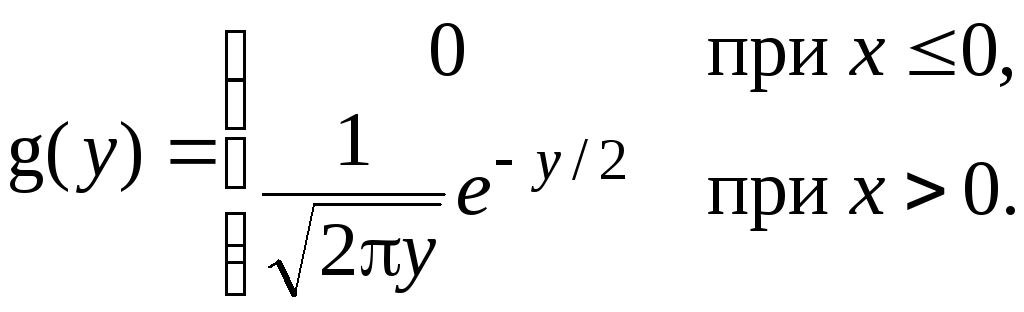
Проверка:

.

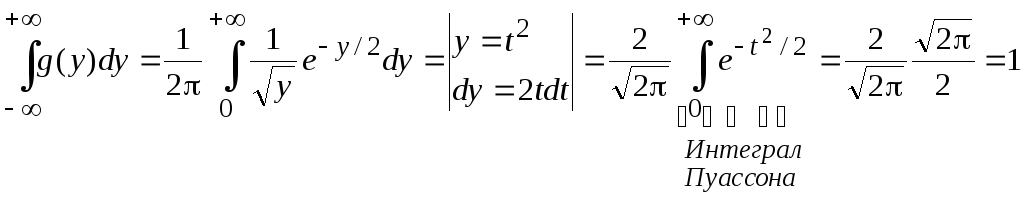10.3. Функции двух случайных величины. Композиция законов распределения.

Если каждой паре возможных значений случайных величин X и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных величин X и Y и записывают в виде Z=(X,Y). Одной из важнейших частных случаев такой функциональной зависимости является сумма независимых случайных величин: Z=X+Y. Нахождение закона распределения суммы случайных величин по известным законам распределения слагаемых называется композицией законов распределения.

Если X и Y – дискретные независимые случайные величины, то для того чтобы найти распределение функции Z=X+Y, надо найти все возможные значения Z, для чего достаточно сложить каждое возможное значение X со всеми возможными значениями Y; вероятности же найденных возможных значений Z равны значениям вероятностей складываемых значений X и Y.

Пример 10.5. Дискретные случайные величины X и Y заданы законами распределения

X	1	3		Y	2	4
P	0,3	0,7		P	0,6	0,4

Найти закон распределения случайной величины Z=X+Y.

Решение. Найдем все возможные значения случайной величины Z и их вероятности: z₁=1+2=3, z₂=1+4=5, z₃=3+2=5, z₄=3+4=7;

P(Z=z1)=0,30,6=0,18,	P(Z=z3)=0,70,6=0,42,
P(Z=z2)=0,30,4=0,12,	P(Z=z1)=0,70,4=0,28.

Напишем искомый распределения, сложив предварительно вероятности несовместных событий: Z=z₂=5 и Z=z₅=5 (P=0,12+0,42=0,54):

Z	3	5	7
P	0,18	0,54	0,28

Пусть X и Y – непрерывные независимые случайные величины и f₁(x), f₂(x), g(x) – плотности распределений случайных величин X, Y и Z=X+Y, соответственно. Найдем сначала функцию распределения случайной величины Z:

F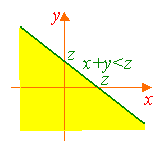(z) = P(Z<z) = P(X+Y<z) = ,

где D – множество всех точек плоскости xOy, координаты которых x и y удовлетворяют неравенству x+y<z; f(x,y) – плотность распределения пары случайных величин (X,Y). Так как X и Y – независимые случайные величины, то f(x,y)=f₁(x)f₂(y) и

.

Чтобы найти плотность распределения, вычислим производную от функции распределения:

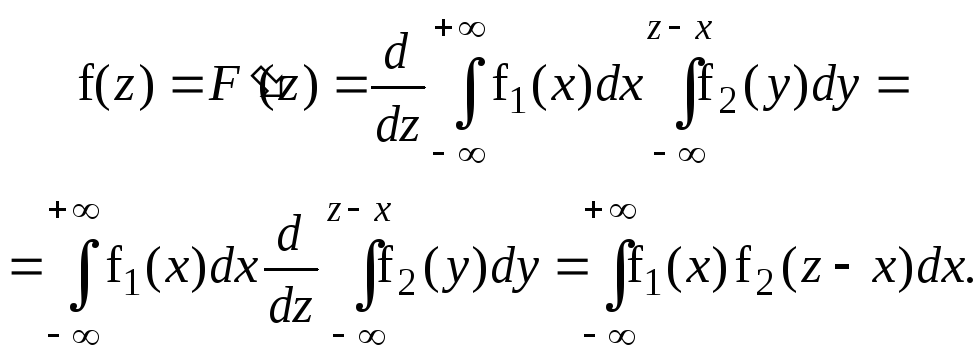
Итак,

. (10.7)

Пример 10.6. Независимые случайные величины X и Y заданы плотностями распределения

Решение. Воспользуемся формулой (10.7) Поскольку f₁(x) и f₂(y) не равны нулю только для неотрицательных аргументов, то

.

Следовательно,

для z(0,+) и g(z)=0 для z(0,+).

10.4. Числовые характеристики функции двух случайных величины.

Здесь мы обобщим некоторые свойства математического ожидания и дисперсии.

Теорема 10.1. Дисперсия суммы двух случайных величин равна сумме их дисперсий плюс удвоенный корреляционный момент:

.

Действительно,

Теорема 10.2. Математическое ожидание произведения двух случайных величин равно произведению их математических ожиданий плюс корреляционный момент:

.

Действительно, исходя из определения корреляционного момента, получим:

Отсюда получаем искомое равенство.

Теорема 10.3. Для независимых случайных величин X и Y справедливо равенство:

.

Доказательство аналогично доказательству теоремы 1.