краткий курс лекций по электростатике

Если считать внешнюю сферу бесконечно большой, то можно определить ёмкость уединенного шара.

Емкость земного шара

Если радиусы сфер близки друг к другу.

5. Ёмкость цилиндрического конденсатора

Er = 2πετ 0 1r ; E = −grad ϕ;

Если радиусы цилиндров близки друг другу

C = 2πεd0 R1l = ε0 dS .

43

6. Соединения конденсаторов

7. Конденсатор конечных размеров

Для реального конденсатора поле не полностью сосредоточено между обкладками На краях пластины наблюдается дополнительная концентрация заряда, что приводит к увеличению емкости. Если пластины представляют собой окружности радиуса R, то емкость вычисляется по формуле Кирхгофа, полученной при R>>d. (Ландау, т.8 стр. 38).

44

Лекция 10

Электростатическая энергия.

1. Энергия системы точечных зарядов

Можно говорить, что эта энергия взаимодействия двух точечных зарядов, находящихся на расстоянии r12 . Если заряды одноименные, то эта энергия

положительна. Если разноименные, то отрицательна.

Пусть поле создано двумя зарядами q1 и q2 и в нем перемещается заряд q3. Рассуждая аналогично, можно показать, что энергия этого третьего заряда равна

Wp3 = k q1q3 + k q2q3 .

r13 r23

Если к этому заряду добавить энергию второго заряда в поле первого, то полная энергия системы этих зарядов равна

Из симметрии формулы видно, что не имеет значения, в каком порядке собиралась данная система. Можно говорить, что эта энергия любого заряда в поле двух других. Однако нельзя считать, что эта энергия принадлежит к какому-то одному из зарядов. Поэтому чаще говорят, что это потенциальная энергия взаимодействия заряда. Она не зависит от того, как собиралась эта система, а зависит только от взаимного расположения зарядов.

В данном выражении не учитывается собственная энергия каждого точечного заряда, как уединенного объекта, т.е. та энергия, которая необходима, чтобы упаковать порции заряда в нулевой объем. Очевидно, что данная энергия бесконечна. Эту энергию достаточно сложно изменить.

45

Поэтому, можно считать, что это величина постоянная, а так как потенциальная энергия определена с точностью до постоянной, то в энергии взаимодействия её можно не учитывать.

Wp = qϕ

2. Энергия заряженного тела

Переходя от дискретного распределения зарядов к непрерывному, из формулы (*) получаем

Wp = 12 ∫ϕdq

Если заряженное тело имеет объём, то dq = ρdV ,

Wp = 12 Vтела∫ ρϕdV

Данное выражение по смыслу отличается от аналогичного для точечных зарядов (*), т.к. здесь собственная энергия уже учитывается.

3. Энергия заряженной сферы

46

ρϕ

Wp = k Q22 R. 2R

Wp = k Q2

2R

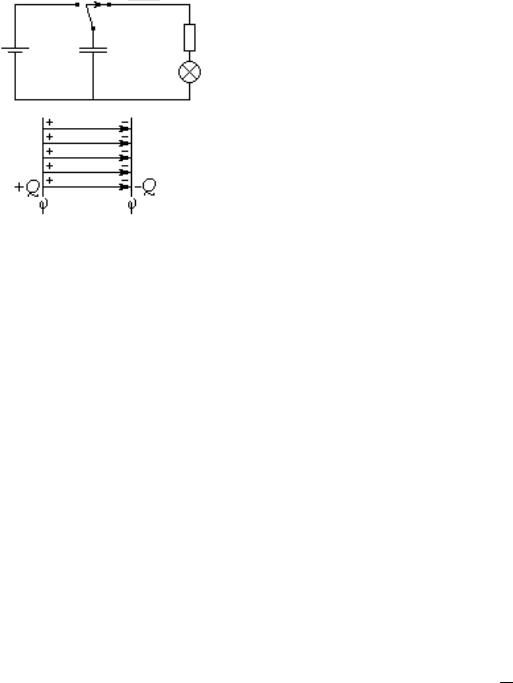
4. Энергия заряженного конденсатора

Данный простой эксперимент показывает, что заряженный конденсатор обладает энергией.

Wp = 12 ∑q1ϕ1 = 12 (Q1ϕ1 +Q2ϕ2 )= 12 Q (ϕ1 −ϕ2 ).

Когда речь идет о конденсаторе, часто используется понятие напряжения. В электростатике понятие разности потенциалов и напряжения совпадают.

5. Энергия заряженной сферы

Исходя из выражения для ёмкости уединенного шара C = Rk , получаем выражения для энергии:

47

Wp = Q2 = k Q2 . 2C 2R

6. Энергия поля

Когда речь идет о заряженном конденсаторе, возникает вопрос: полученная энергия – это энергия зарядов на пластинах конденсатора или энергия поля, сосредоточенного между пластинами конденсатора. В рамках электростатики на данный вопрос ответить нельзя, т.к. нет поля без заряда. Ответ будет дан при изучении электродинамики, а здесь выразим полученную ранее энергию через характеристики поля, на примере плоского конденсатора.

Обобщая полученное выражение можно записать, что энергия электростатического поля в некотором объёме равна:

Здесь w – объёмная плотность энергии.

7. Энергия заряженной сферы

8. Классический радиус электрона

Найдем энергию заряженного шара.

Энергию поля снаружи можно найти по формуле

48

Wp = k 2Q2R

ε1

Аналогично рассчитаем энергию поля внутри шара

Таким образом, полная энергия

Если в качестве шара рассматривать электрон в вакууме, то тогда

На этом изучение раздела «электростатика» закончим.

49

Лекция 11

Постоянный ток. Основные понятия и законы постоянного тока.

1. Понятие о токе

Определение: Направленное (упорядоченное) движение заряженных частиц называется электрическим током.

Если речь идет о движении микрочастиц, то говорят о токе проводимости. А, если о движении макрочастиц, то говорят о токе конвекции.

Исторически сложилось, что за направление тока принимают направление движения положительно заряженных частиц.

2. Плотность тока и сила тока

Для характеристики постоянного тока вводят две физические величины: векторную – плотность тока и скалярную – сила тока.

Определение: Плотностью тока называется физическая величина, определяющая заряд, прошедший через площадку dS за время dt следующим образом.

dQ = ( j, n)dSdt.

Пусть все частицы одинаковые и имеют заряд q и скорость υ, которая называется средней или упорядоченной или дрейфовой скоростью.

dQ = dN = qndV = qn(dSn,υdt ) = (qnυ, n)dSdt,

Определение: Силой тока называется поток плотности тока через какуюлибо поверхность.

50

Силу тока можно определять как заряд, прошедший через поперечное сечение проводника за время ∆t. Данное выражение используется для определения единицы заряда.

3. Единицы силы и плотности тока

Определение: 1 Ампер – единица СИ электрического тока, равная силе такого неизменяющегося тока, который при прохождении по двум бесконечно длинным проводникам ничтожно малой площади поперечного сечения вызывает силу взаимодействия между ними 2·10-7 Н на 1 м длины.

Плотность тока измеряется в А/м2.

4. Действия электрического тока

Непосредственно наблюдать электрический ток нельзя. О его существовании судят по макроскопическим проявлениям.

Закон сохранения заряда утверждает, что в замкнутой системе заряд сохраняется. Если система не замкнута, то заряд может изменяться.

−dQ = ∫( j, n)dSdt. dQdt + ∫(j, n)dS = 0

Данное уравнение называется уравнением непрерывности в интегральной форме. Производная по времени связана с временной зависимостью заряда. Данное уравнение считается постулатом. По смыслу – это закон изменения заряда.

51

Используя понятие объемной плотности заряда и формулу Остроградского-Гаусса

Q = ∫ρdV ; ∫( j, n )dS = ∫divjdV

получаем

∂∂ρt + div j = 0

– уравнение непрерывности в дифференциальной форме.

плотности тока являются замкнутыми.

6. Поле в проводнике при постоянном токе

Если есть ток, значит, есть движение зарядов, следовательно, есть сила, которая заставляет двигаться заряды, есть ток, есть напряженность, которая направлена вдоль тока. В общем случае напряженность направлена под углом к поверхности. Если есть напряженность, то градиент потенциала вдоль проводника не равен нулю, следовательно, потенциал вдоль проводника изменяется. Говорят о падении потенциала.

7. Закон Ома в дифференциальной форме

Плотность тока и напряженность вдоль проводника взаимосвязаны между собой. Разумно предположить, что это самая простая связь, т.е. линейная.

j =σ E

где σ – удельная электропроводность. Данный закон является постулатом.

Для металлов закон выполняется почти всегда, для полуметаллов начинаются отклонения при очень больших плотностях тока. Для других линейную связь можно заменить тензорной и закон Ома замыкает уравнения Максвелла.

Из этого соотношения следует, что линии плотности тока и линии напряженности при постоянном токе совпадают, а, следовательно, распределение полей можно изучать по распределению тока (метод электролитической ванны).

52