0. 5.2. Простые числа и их свойства

Определение 5.2. Натуральное число n>1 называется простым, если оно имеет в точности два различных натуральных делителя – 1 и n, в противном случае n называется составным.

Пример 5.4 Числа 2,3,7 являются простыми. Числа 4,6,8 – составными, так как их делителем является число 2.

Свойства простых чисел:

1. Если p₁ и p₂ – простые и 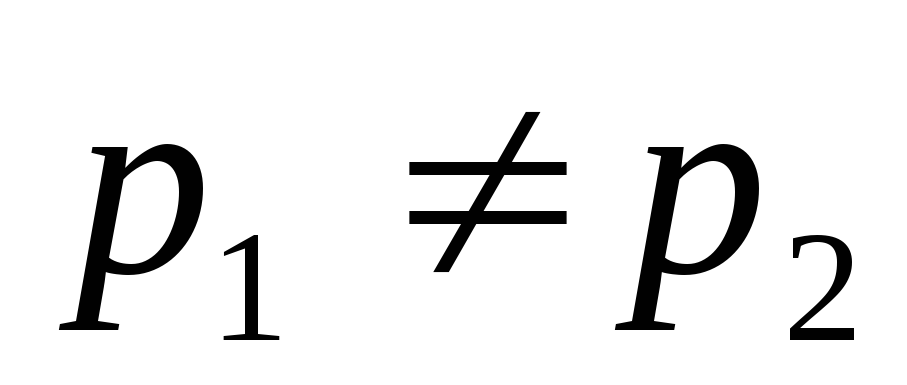, тоp₁ не делится на p₂.

2. Пусть p – простое число, а n – натуральное, тогда n делится на p или наибольший общий делитель чисел n и p равен 1.

3. Если 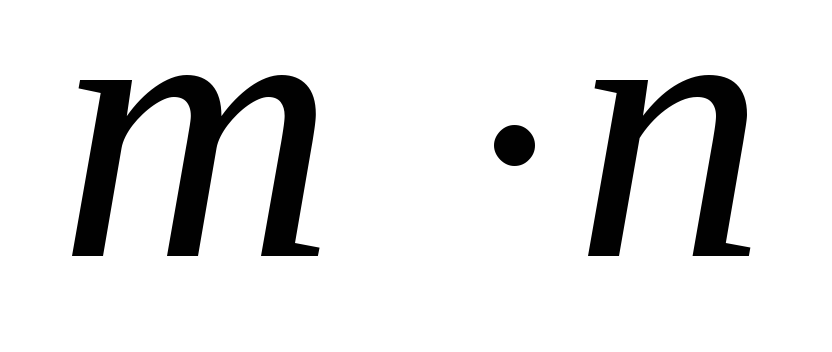делится на простое число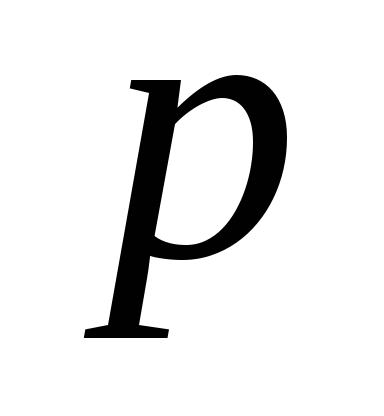, тоm делится на p или n делится на p.

4. Если делится на простое число, то существует, которое делится на.

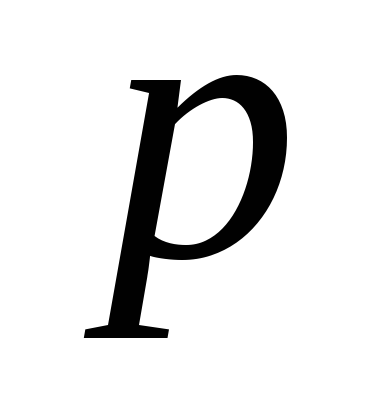Известна следующая теорема:

Теорема 5.1. Любое натуральное число n>1 либо просто, либо раскладывается в произведение простых чисел и притом единственным образом с точностью до порядка следования сомножителей: , где. Данное разложение называют канонической формой числаn.

Задача представления числа n в канонической форме называется задачей факторизации числа n.

Существенный с точки зрения криптографии факт состоит в том, что в арифметике не известно эффективного алгоритма факторизации числа n. Никаких эффективных методов неизвестно даже в таком простом случае, когда необходимо найти два простых числа p и q, таких, что .

Известен ряд подходов, позволяющих выполнить проверку простоты целого числа n – решето Эратосфена, критерий Вильсона, тестирование на основе малой теоремы Ферма, тест Соловея-Штрассена, тест Рабина-Миллера и др.

Наибольшим общим делителем целых чисел a и b, обозначаемым как НОД(a,b) или просто (a,b), называют наибольшее целое, делящее одновременно числа a и b. Если (a,b)=1, то a и b называют взаимно простыми.

0. 5.3. Числовые функции

В теории чисел и в криптографии большое значение имеют следующие числовые функции [8, 20].

- определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая: .

- определяет количество всех делителей числа n.

Пусть канонической формой числа n является . Тогда.

- определяет сумму всех делителей числа n,

- функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,

(5.1)

Пример 5.5

Для числа n=720 найдем ,,.

Представим число 720 в канонической форме - .

Тогда

0. 5.4. Выводы

Сравнимость по модулю, понятие простых, взаимно простых чисел, а также числовые функции имеют очень большое значение для криптографии, в частности при построении асимметричных шифров.

0. 5.5. Вопросы для самоконтроля

1. Дайте определение сравнимости по модулю.

2. Приведите примеры чисел, сравнимых с 5 по модулю 7.

3. Что называют полным набором вычетов по модулю?

4. Перечислите основные свойства сравнений.

5. Дайте определение простого и составного числа. Приведите примеры.

6. Что называют канонической формой числа n.

7. В чем заключается задача факторизации числа n.

8. Факторизуйте следующие числа: 200, 143, 89.

9. Дайте определение наибольшего общего делителя чисел a и b.

10. Найдите наибольший общий делитель следующих чисел – 10 и 4, 20 и 21, 3 и 90.

11. Какие числа называют взаимно простыми? Приведите примеры взаимно простых чисел.

12. Найти ,,.
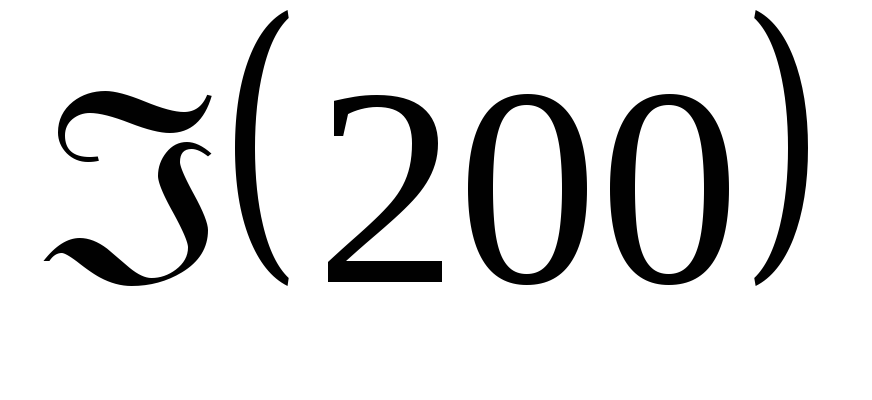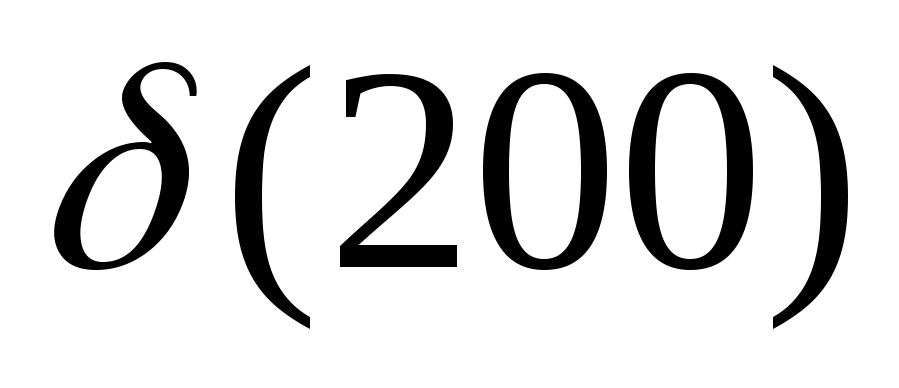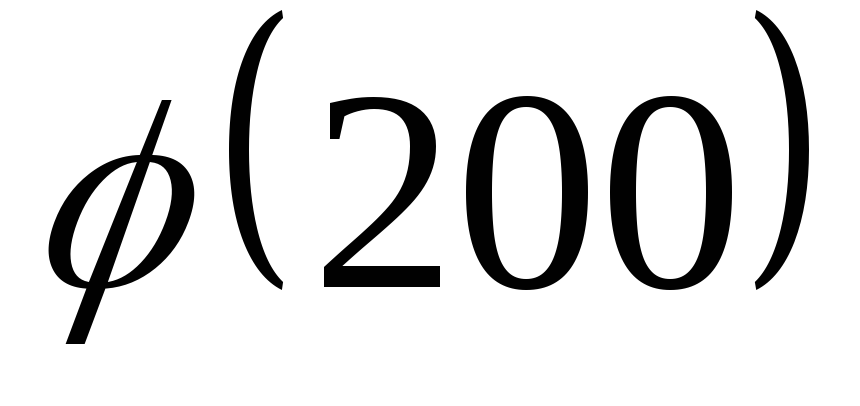