теория колебаний 2
.doc
Вопросы по теории колебаний (2-й тест)
1.Вынужденные колебания это
@движения под действием внешнего периодического источника энергии
1.Параметрические колебания это
@движение, вызванное изменением энергоемкого параметра за счет внешнего источника
1.Автоколебания это
@движение у которого амплитуда, форма и частота зависит только от внутреннего 1. Постоянная времени это
@временной интервал в течение которого амплитуда уменьшается в е—раз
1. Логарифмически декремент затухания определяется как
@натуральный логарифм отношения текущей амплитуды к амплитуде через условный
1. Коэффициент затухания это
@величина обратная постоянной времени
1. Особая точка это
@точка, через которую проходит несколько интегральных кривых
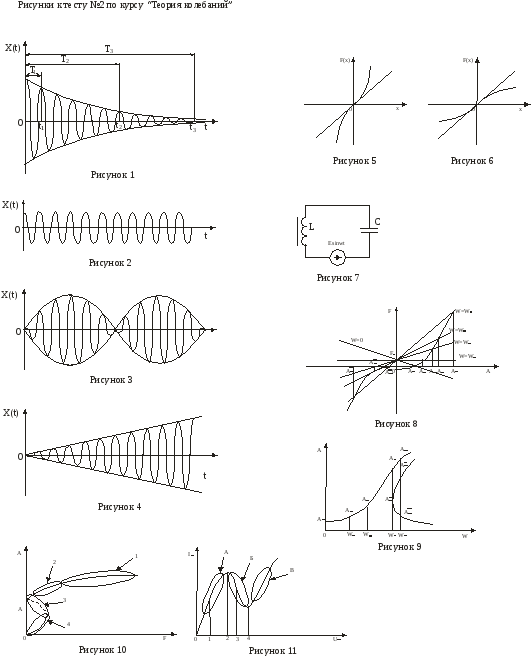
1. Логарифмический декремент затухания (см. рисунок 1) можно рассчитать по следующей формуле
@Формула 1
1. Система уравнений (4) описывает
@систему с кулоновским трением
1. Состояние равновесия устойчиво по Ляпунову
@если система совершает колебания вблизи состояния
1. Состояние равновесия абсолютно устойчиво
@если система с течением времени возвращается в состояние равновесия
1. Оцените устойчивость системы, если корни характеристического уравнения имеют вид (см. формулу 5) и выполняются условия (6)
@система неустойчива
1. Оцените устойчивость системы если корни характеристического уравнения имеют вид (см. формулу 5) и выполняются условия (7)
@система устойчива по Ляпунова
1. Система уравнений (8) описывает
@нелинейную систему N-го порядка
1. Система первого приближения получается из системы уравнений (9) после отброса
@нелинейных членов, чей порядок не превышает второго порядка малости
1. Если все корни характеристического уравнения системы первого приближения имеют @асимптотически устойчиво
1. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с положительной вещественной частью, то соответствующее состояние равновесия нелинейной системы
@неустойчиво
1. Если среди корней характеристического уравнения системы первого приближения встречается хотя бы один корень с нулевой вещественной частью, то соответствующее состояние равновесия нелинейной системы
@ невозможно сделать заключение об устойчивости или неустойчивости исходной системы
1.Уравнение (10) описывает
@колебания в линейной системе при внешнем воздействии
1.Уравнение (11) описывает
@колебания в нелинейной системе при внешнем воздействии
1.Уравнение (12) описывает
@общее решение неоднородного дифференциального уравнения
1.Первый член уравнения (13) соответствует
@решению уравнения (10) при
![]()
1.Второй член уравнения (13) соответствует
@частному решению уравнения (10)
1.Общим решением неоднородного дифференциального уравнения является
@Уравнения (13)
1.Принцип суперпозиции применим для рассмотрения
@вынужденных колебаний в линейных системах
1. Решение уравнения (14) может быть найдено методом
@комплексных амплитуд
1. Уравнение (15) описывает
@вынужденные колебания в линейной системе при гармоническом воздействии
1. Метод комплексных амплитуд применим для анализа
@вынужденные колебания в линейной системе при гармоническом воздействии
1. Суть метода комплексных амплитуд заключается в том, что решение уравнения (14) сводится
@к решению уравнения (16)
1. Комплексная амплитуда вынужденных колебаний в линейной системе описывается
@формулой 20
1. Амплитудно─частотная характеристика линейной системы описывается
@формулой 19
1. Фазо─частотная характеристика линейной системы описывается
@формулой 21
1. Амплитуда вынужденных колебаний в линейной системе определяется
@формулой 19
1. Амплитуда вынужденных колебаний в линейной системе определяется
@формулой 21
1. При воздействии на линейную систему
внешней гармонической силы с частотой
![]() в
системе возбуждаются колебания
в
системе возбуждаются колебания
@с частотой
![]()
1. Резонансом называется
@явление резкого увеличения амплитуды вынужденных колебаний на некоторой частоте
1. Биениями в колебательной системе называется
@явление взаимодействия собственных колебаний системы с колебаниями внешнего источника
1. Уравнение (22) описывает вынужденные колебания
@в линейной системе при включении источника гармонических колебаний
1. В формуле (22), 1 и 2 члены уравнения описывают
@решение однородного дифференциального уравнения
1. В формуле (22), 3 член уравнения описывает
@частное решение неоднородного дифференциального уравнения
1.Колебания в системе описанной формулой (22) имеют вид
рисунок 2
рисунок 3
рисунок 4
1. При воздействии на линейную систему
источника гармонических колебаний с
частотой
![]() вынужденные колебания имеют вид
вынужденные колебания имеют вид
рисунок 2
рисунок 3
рисунок 4
1. При воздействии на линейную систему
источника гармонических колебаний с
частотой
![]() вынужденные колебания имеют вид
вынужденные колебания имеют вид
рисунок 2
рисунок 3
рисунок 4
1. Частота высокочастотного колебания сигнала биений (рисунок 3) равна
@![]()
1. Частота вынужденных колебания (рисунок
3), на линейную систему, при воздействии
внешнего источника с частотой
![]() (рисунок 2) равна
(рисунок 2) равна
@![]()
1. Гармонический осциллятор при произвольном внешнем воздействии может быть описан дифференциальным уравнением вида
@формула 23
1.. Частное решение для гармонического осциллятора ищется в виде
@формула 17
1. Метод вариации постоянной Лагранжа основан на том, что решение ищется в виде
гармонического колебания с частотой внешнего воздействия
@гармонического колебания с резонансной частотой
1. Уравнение связи функции
![]() с функциями
с функциями
![]() и
и
![]() в
формуле (17) может быть получено из формулы
(24) путем
в
формуле (17) может быть получено из формулы
(24) путем
@приравнивания к нулю 3 и 4 члена уравнения (24)
1. Уравнение связи функции
![]() с функциями
с функциями
![]() и
и
![]() (условие
Лагранжа) имеет вид
(условие
Лагранжа) имеет вид
@уравнение 2 в системе (25)
1. Производные
![]() и
и
![]() могут быть найдены из системы (25) путем
могут быть найдены из системы (25) путем
@решения системы алгебраических уравнений
относительно
![]() и
и
![]()
1. Уравнение (26) может быть записано в
виде (27) если функция
![]() является
является
@нечетной
1. Уравнением Дуффинга является
@уравнение (27)
1. Уравнение (27) описывает колебательный процесс в
колебательном контуре
@математическом маятнике
1.Задача Дуффинга может быть решена
@методом гармонического баланса
1. Для анализа автоколебательных систем пользуются
@методом медленно меняющихся амплитуд
1. Используя формулу (29) определите к какому типу относится колебательная система
с «жесткой» характеристикой упругой силы
@с «мягкой» характеристикой упругой силы
1. Используя рисунок (7) определите к какому типу относится колебательная система
@с «жесткой» характеристикой упругой силы
1. Используя рисунок (5) определите к какому типу относится колебательная система
@с «жесткой» характеристикой упругой силы
1. Используя рисунок (6) определите к какому типу относится колебательная система
@с «мягкой» характеристикой упругой силы
1. Используя рисунок (5) определите
значение коэффициента
![]() в уравнении (27)
в уравнении (27)
@![]()
1. Используя рисунок (5) определите
значение коэффициента
![]() в уравнении (27)
в уравнении (27)
@![]()
1. Метод гармонического баланса применим для
@нелинейных систем при
![]()
1. При использовании метода гармонического баланса решение уравнения (27) ищется в виде
@формула (30)
1. Метод гармонического баланса применим для нелинейных систем при
@гармоническом воздействии
1. При анализе системы методом гармонического баланса
@отыскивается установившееся колебание
1. В уравнении (31) укажите слагаемое от которое определяет точность решения
@3─е слагаемое
1. В уравнении (31) укажите какие из слагаемых необходимо приравнять к нулю чтобы найти (А,Ф)
@1 и 2
1. Пользуясь рисунком (8) укажите частоты на которых существует неоднозначность амплитуд
@![]()
1. Пользуясь рисунком (8) укажите частоты на которых происходят скачки фаз
@![]()
1. Какая из отмеченных на рисунке 10 областей является рабочей для феррорезонансных стабилизаторах напряжения.
@Область 1
1. Какая из отмеченных на рисунке 11 областей является рабочей для генератора на туннельном диоде
@Область Б
1. Какая из отмеченных областей (рисунок 11) является участком с отрицательным сопротивлением.
@Область Б
1. Пользуясь рисунком 11 укажите на вольт─амперной характеристике рабочую точку туннельного диода
@3
1. Укажите условие самовозбуждения лампового генератора
@формула 37
1. Укажите условие при котором самовозбуждение лампового генератора невозможно
@формула 36
1. Укажите условие при котором на выходе лампового генератора установятся автоколебания с постоянной амплитудой
@формула 38
1. Укажите условие самовозбуждения автогенератора на туннельном диоде
@формула 39
1. Укажите условие при котором самовозбуждение автогенератора на туннельном диоде невозможно
@формула 41
1. Укажите условие при котором на выходе автогенератора на туннельном диоде установятся автоколебания с постоянной амплитудой
@формула 40
Формулы и рисунки к вопросам по курсу «Теория колебаний» (Часть II)
1.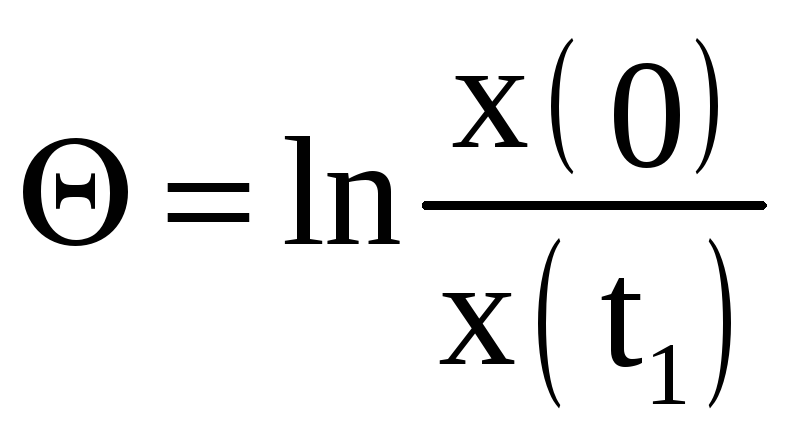 2.
2.
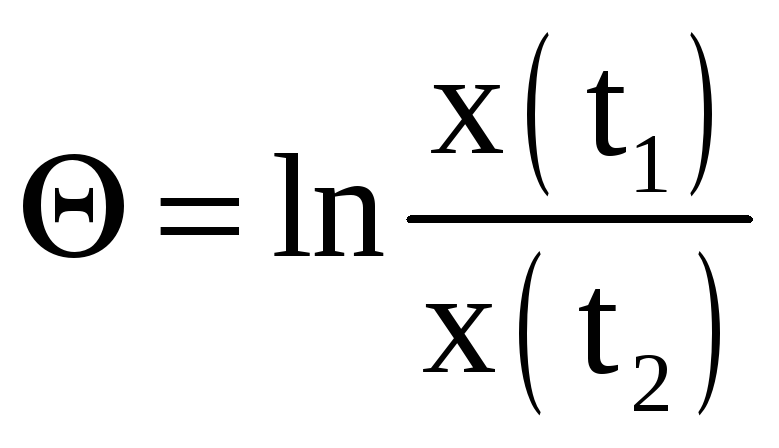 3.
3.
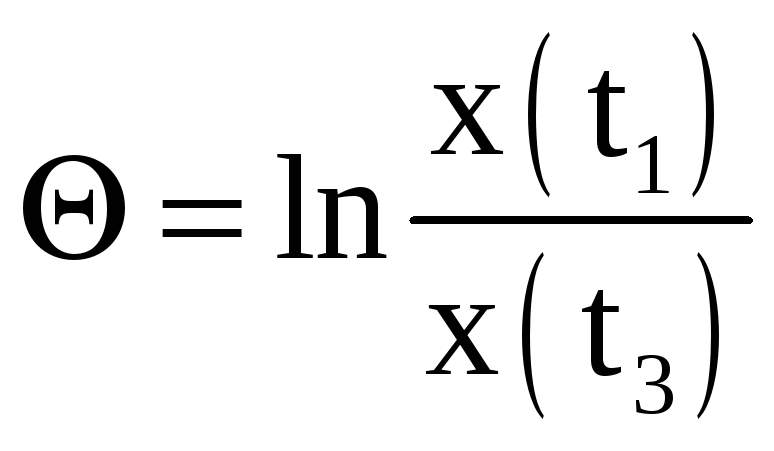 4.
4.
![]()
5.
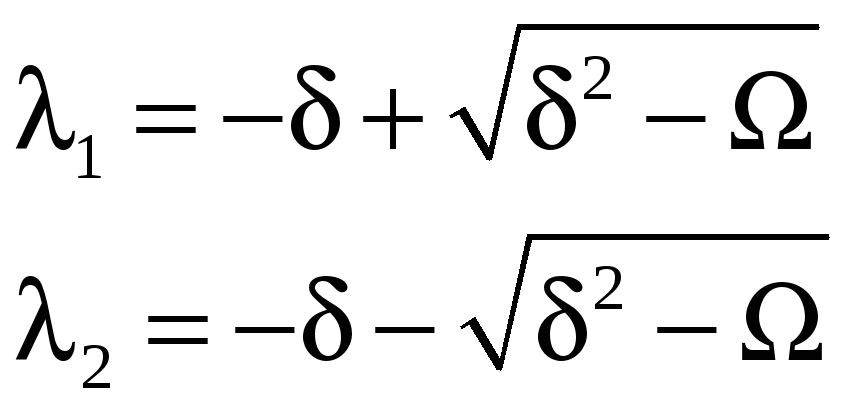 6.
6.
![]() ,
,
![]() 7.
7.
![]() ,
,
![]()
8.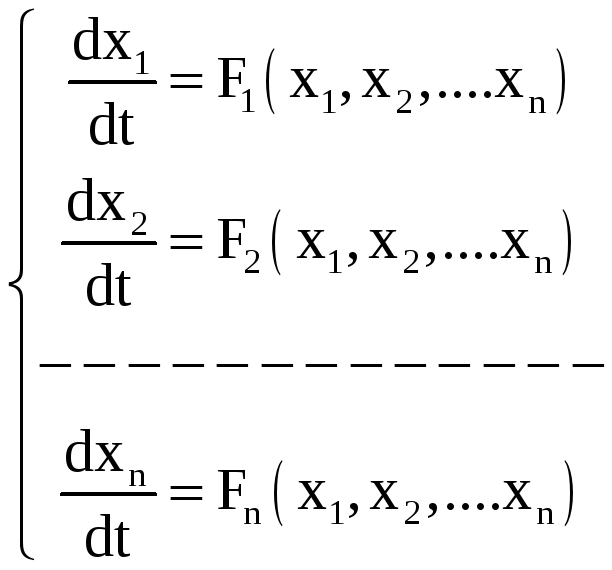
9.
 10.
10.![]() 11.
11.
![]() 12.
12.![]()
13.
![]() 14.
14.
![]()
15.![]() 16.
16.![]()
17.
![]() 18.
18.
![]()
19.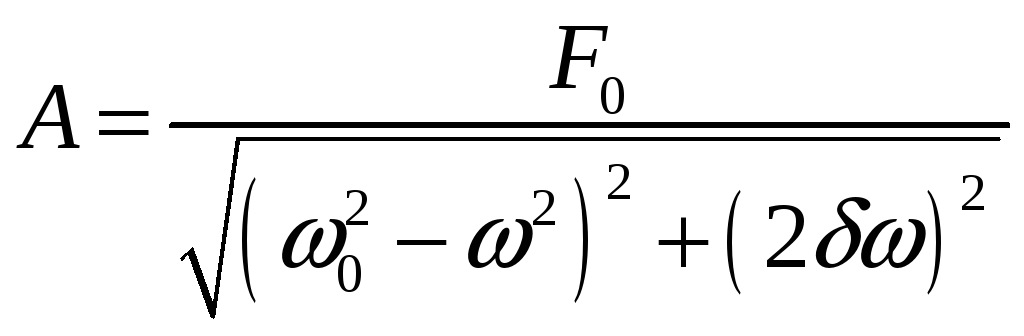 20.
20.
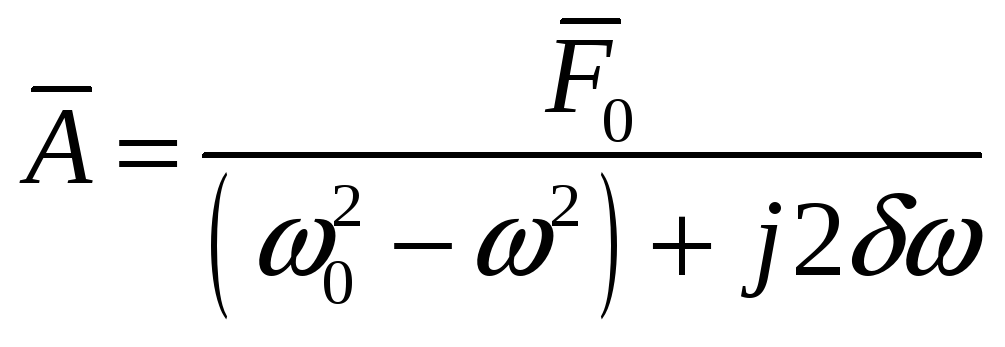 21.
21.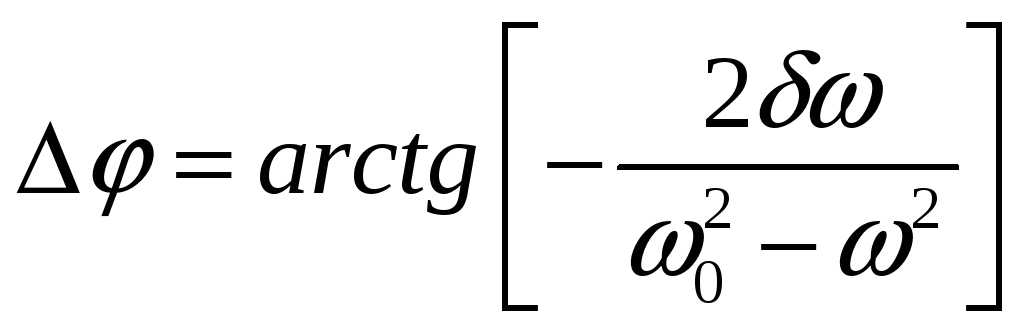
22.![]()
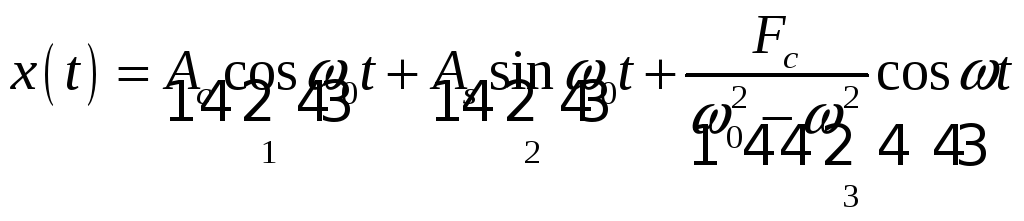 23.
23.
![]()
24.
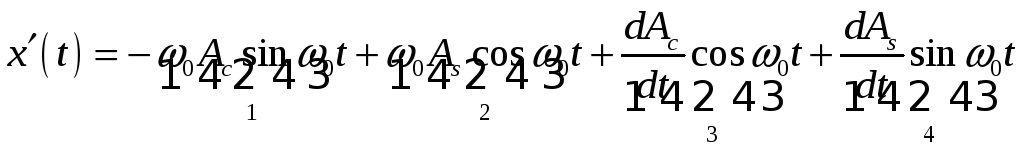
25.
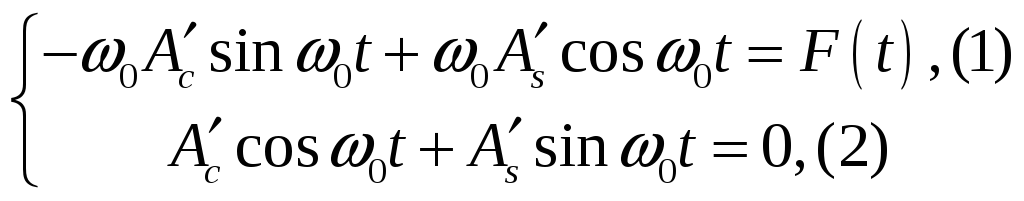
26.
![]() 27.
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
31.
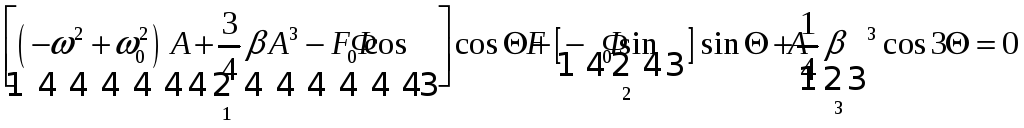
32.
![]() 33.
33.
![]() 34.
34.
![]() 35.
35.
![]()
36.
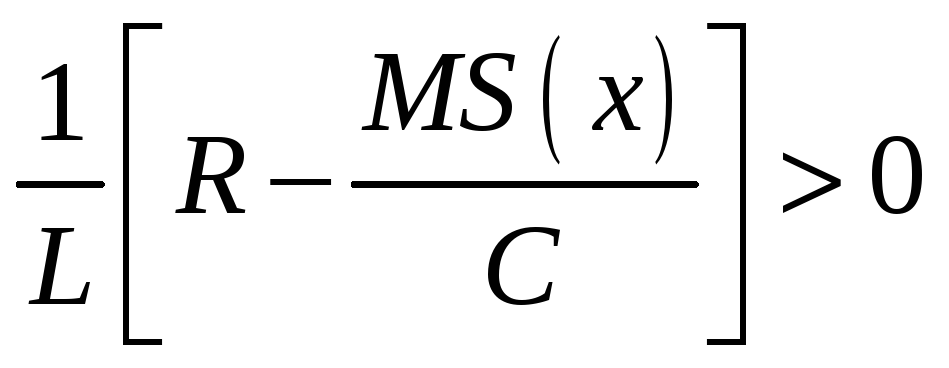 37.
37.
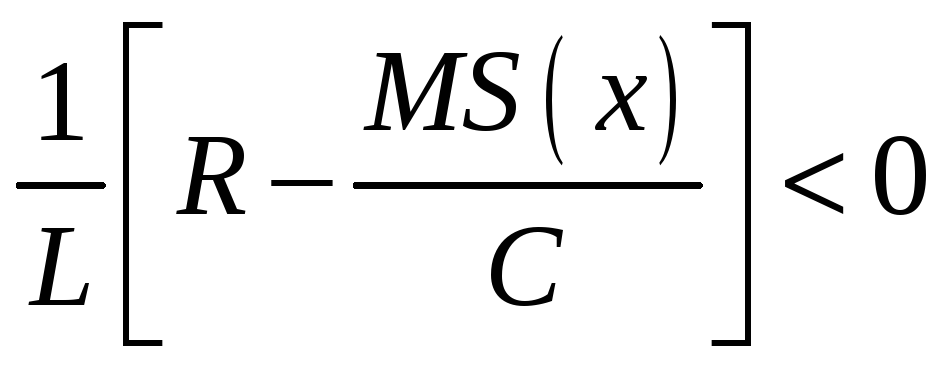 38.
38.
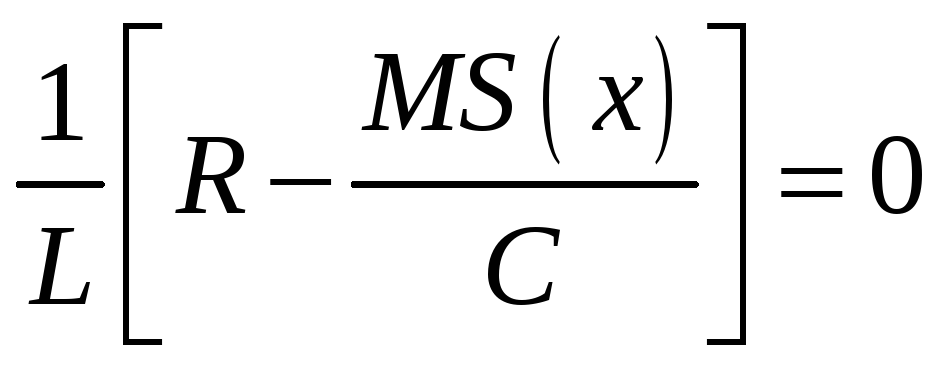
39.![]() 40.
40.
![]() 41.
41.
![]()