
- •УЧЕБНОЕ ПОСОБИЕ
- •Предисловие
- •1. Свободное программное обеспечение
- •1.1. Основные сведения о свободном программном обеспечении
- •1.2. Офисный пакет OpenOffice.org
- •Краткое описание
- •Установка пакета OpenOffice.org
- •Первый запуск OpenOffice.org
- •1.3. Электронные таблицы Gnumeric
- •1.4. Математический пакет Maxima
- •1.5. Пакет для статистических и эконометрических расчетов Gretl
- •2. Линейная алгебра и аналитическая геометрия
- •2.1. Примеры решения задач линейной алгебры при помощи электронных таблиц Gnumeric
- •Задача 2.1. Умножение матриц
- •Задача 2.2. Вычисление определителя
- •Задача 2.3. Вычисление обратной матрицы
- •3. Математический анализ
- •3.1. Программа Maxima как научный калькулятор
- •3.2. Задачи на нахождение пределов
- •3.4. Производная. Исследование функций
- •Задача 3.7. Поиск экстремумов.
- •Задача 3.8. Минимаксная задача.
- •Задача 3.9. Исследование функции и построение ее графика.
- •3.5. Интеграл
- •Задача 3.10. Неопределенный интеграл.
- •Задача 3.11. Определенный интеграл.
- •Задача 3.12. Несобственный интеграл.
- •3.7. Ряды
- •Задача 3.13. Сходимость и суммы числовых рядов.
- •Задача 3.14. Сходимость числового ряда.
- •Задача 3.15. Сходимость степенного ряда.
- •Задача 3.16. Разложение в ряд Тейлора.
- •3.8. Дифференциальные уравнения
- •Задача 3.18. Задача Коши.
- •4. Теория вероятностей и математическая статистика
- •4.1. Задачи теории вероятностей
- •Задача 4.1. Задача о лотерейных билетах.
- •Задача 4.2. Задача о днях рождения.
- •Задача 4.3. Задача об отказах. Распределение Пуассона.
- •Задача 4.4. Нормальное распределение.
- •4.2. Задачи математической статистики
- •Задача 4.5. Расчет доверительных интервалов.
- •Задача 4.6. Проверка гипотезы о равенстве средних
- •Задача 4.7. Проверка гипотезы о равенстве дисперсий
- •Задача 4.8. Проверка гипотезы о виде закона распределения.
- •5.1. Системы массового обслуживания
- •5.2. Линейное, целочисленное и нелинейное программирование
- •5.3. Задачи экономического моделирования
- •Задача 5.1. Система массового обслуживания.
- •Задача 5.2. Задача линейного программирования.
- •Задача 5.3. Транспортная задача
- •Задача 5.4. Задача о назначениях
- •Задача 5.5. Модель Леонтьева межотраслевого баланса
- •Задача 5.6. Формирование портфеля ценных бумаг
- •6. Эконометрика
- •6.1. Основные положения
- •6.2. Краткое описание пакета программ Gretl
- •6.3. Множественная регрессия
- •Расчет основных статистик.
- •Анализ корреляционной матрицы. Выбор значимых факторов.
- •Сравнение цен по городам
- •Проверка нормальности и гомоскедастичности остатков
- •Выводы
- •6.4. Анализ временных рядов
- •Выбор линии тренда
- •Автокорреляция остатков (прямые расчеты)
- •Авторегрессия
- •Сезонные колебания
- •6.5. Системы одновременных эконометрических уравнений
- •Заключение
- •Библиографический список
- •МАТЕМАТИКА В ЭКОНОМИКЕ
- •УЧЕБНОЕ ПОСОБИЕ
- •МАТЕМАТИКА В ЭКОНОМИКЕ
- •УЧЕБНОЕ ПОСОБИЕ
4. Теория вероятностей и математическая статистика
4.1. Задачи теории вероятностей
Задача 4.1. Задача о лотерейных билетах.
В партии из 19 лотерейных билетов 9 выигрышных. Куплено
12 билетов. Какова вероятность, что среди них 7 выигрышных?
Решение. Здесь используется гипергеометрическое распреде-
ление.
Вероятность того, что при покупке n билетов из партии объе-
мом N, в которой имеется D выигрышных, мы получим d выигрыш-
|
|
|
d n |
d |
|
|
|
||
ных, равна |
p |
|
CDCN |
D |
. |
|
|
||
|
CNn |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
Здесь |
|
Cnm |
|
n! |
|
|
- биномиальный коэффициент, а |
||
|
|
|
|
|
|
||||
|
m!(n |
m)! |
|||||||
|
|
|
|
|
|||||
n! 1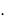 2
2 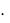 ...
... (n 1)
(n 1) 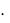 n, причем 0! 1! 1.
n, причем 0! 1! 1.
Для расчетов воспользуемся программой Maxima.
Биномиальный коэффициент вычисляется при помощи функ-
ции binomial(n,m), где n, m имеют тот же смысл, что и выше.
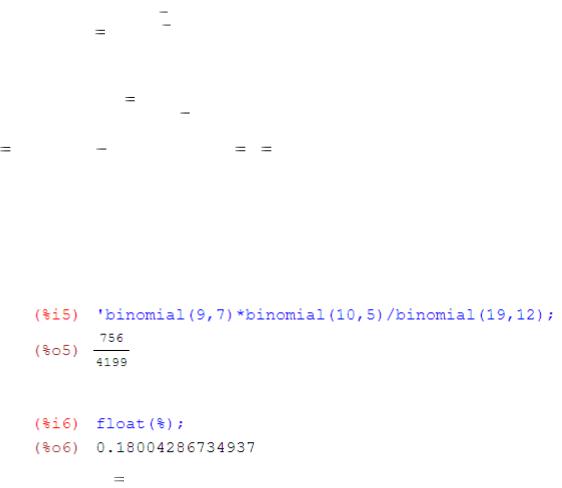
Вводим команду:
Приводим к десятичному виду:
Ответ: p 0.18
99
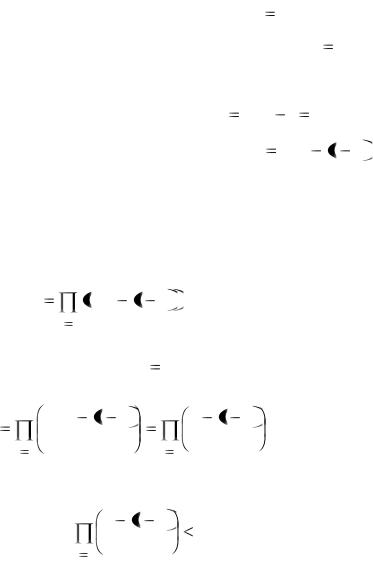
Задача 4.2. Задача о днях рождения.
Сколько человек должно быть в группе, чтобы вероятность
совпадения дней рождения хотя бы у двух человек превышала 0,5?
Решение. Найдем дополнительную вероятность, т.е. вероят-
ность того, что ни у какой пары студентов нет совпадающих дней
рождения.
Пусть в группе n студентов. Всего количество размещений k
дней рождения по 365 дням года равно r 365n .
Первый человек в группе может иметь m1 365 вариантов дня рождения. 2-ой, для того, чтобы его день рождения не совпал с днем
рождения первого, может иметь m2 |
365 |
1 |
364 варианта дня ро- |
|||||||||||
ждения, ..., i -й человек может иметь mi |
365 |
i 1 варианта дня |
||||||||||||
рождения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Всего вариантов выбора разных дней рождения у n человек |
||||||||||||||
имеется |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
365 |
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
Вероятность равна p |
|
m |
|
или |
|
|
|
|
||||||
|
r |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
365 i |
1 |
|
|
n |
1 i |
1 |
|
|
|
|||
p |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
365k |
|
|
i 1 |
365 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||||
Нам нужно решить следующее неравенство относительно n:
n |
1 i 1 |
|
1 |
|
|
|
|
. |
|||
i 1 |
365 |
2 |
|||
|
|||||
|
|
|
|
||
При этом нас будет интересовать наибольшее приближение к числу ½.
100

Для решения этого неравенства снова используем программу
Maxima.
К сожалению, напрямую решить это неравенство нам не удаст-
ся (необходимо составлять хоть и небольшую, но программу, что выходит за рамки данной книги).
Тем не менее, можно применить универсальный метод после-
довательного приближения.
Определим функцию:
Эта функция считает необходимую нам вероятность. Вычис-
лим эту вероятность при нескольких значениях параметра n – коли-
честве студентов в группе.
Очень мало.
Наоборот, очень много. Делим, далее, интервалы пополам.
Похоже, ближе уже не подобраться. Попробуем число 22:
101

Перебор.
Итак, мы получили, что при 23 студентах в группе вероятность того, что хотя бы у двух из них совпадут дни рождения, превысит
0,5.
Ответ: 23 человека
Задача 4.3. Задача об отказах. Распределение Пуассона.
В цехе имеется n=100 станков. Количество отказов k за смену подчиняется закону Пуассона с параметром =0.34. Найти вероят-
ность того, что количество станков, находящихся в ремонте удовле-
творяет неравенству 3 k 5.
Решение. Закон Пуассона: вероятность k отказов равна
k
pk  k! e
k! e
Вероятность того, что m1 k m2 , равна
|
m2 |
m2 |
k |
|
P(m1 k m2 ) |
pk |
e |
|
|
k! |
||||
k |
m |
k m |
||
|
1 |
1 |
|
Зададим функцию:
Вычисляем при заданных нам значениях:
Ответ: p 0.005
102
