Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Алтайский государственный технический университет им. И.И.Ползунова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

neopred_int(математика)

.pdf

Скачиваний:

Добавлен:

14.02.2015

Размер:

1.18 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Д.А. Мустафина, И.В. Ребро,С.Ю. Кузьмин, С.Г. Антипина

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ВОЛЖСКИЙ ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ (ФИЛИАЛ)

Д.А. Мустафина, И.В. Ребро, С.Ю. Кузьмин, С.Г. Антипина

ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Допущено Научно-методическим советом по математике Министерства образования и науки Российской Федерации в качестве учебного пособия (справочника) для студентов технических направлений и специальностей высших учебных заведений

РПК “Политехник” Волгоград 2006

УДК 519.2

Рецензенты:

кафедра «Математического анализа и теории функций», доктор физ.- мат. наук, профессор, декан МФ Лосев А.Г.

доктор техн. наук, профессор, зав. кафедрой «Информатика, теоретическая механика и ОНИ» Кузнецов Н.Г.

Мустафина Д.А., Ребро И.В., Кузьмин С.Ю., Антипина С.Г. Интегральное исчисление функции одной переменной: Учеб. пособие / ВолгГТУ. – Волгоград, 2006. – 96 с.

ISBN 5 – 230 –

Содержит необходимый теоретический материал и примеры, иллюст-

рирующие основные понятия по учебной дисциплине ″Интегральное ис-

числение функции одной переменной″. Разработаны варианты контрольных (семестровых) работ.

Рассчитано на студентов дневной и вечерней форм обучения высших технических заведений всех специальностей и направлений.

Табл. 11. Библиогр.: 11 названий

Печатается по решению редакционно-издательского совета Волгоградского государственного политехнического университета.

ISBN 5 – 230 –

Волгоградский

государственный

технический университет, 2006

Оглавление

Оглавление . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
§1. Неопределенный интеграл
1.1. Основные понятия неопределённого интеграла . . . . . . . . . . .	4-5
1.2. Основные методы интегрирования
метод непосредственного интегрирования . . . . . . . . . . . . . . . . . . .	5-6
замена переменной . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	6-7
интегрирование по частям . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	7-11
1.3. Интегрирование рациональных дробей . . . . . . . . . . . . . . . . . .	11-16
1.4. Интегрирование тригонометрических функций . . . . . . . . . . .	16-19
1.5. Интегрирование иррациональных функций . . . . . . . . . . . . . .	20-25
1.6. Примеры интегралов, не выражающихся через элементар-
ные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	25-26
1.7. Задания для самопроверки №1 . . . . . . . . . . . . . . . . . . . . . . . . .	27-28
§2. Определённый интеграл
2.1. Основные понятия и методы решения определённого ин-	29-32
теграла
2.2. Приближённое вычисление определённого интеграла
формула прямоугольников . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	32-33
формула трапеций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	33-34
формула парабол (формула Симпсона или квадратурная формула)	34-36
2.3. Несобственные интегралы . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	36-38
2.4. Задания для самопроверки №2 . . . . . . . . . . . . . . . . . . . . . . . . .	38-39
2.5. Геометрические приложения определённого интеграла . . . . .	39-43
2.6. Физические приложения определённого интеграла. . . . . . . . .	44-48
2.7. Экономическое приложение определенного интеграла . . . . .	48-50
2.8. Химическое приложение определенного интеграла . . . . . . . .	50-52
2.9. Задания для самопроверки №3 . . . . . . . . . . . . . . . . . . . . . . . . .	53-55
Вопросы и предложения для самопроверки . . . . . . . . . . . . . . . . . . . .	55-56
Семестровые работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	57-86
Приложение № 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	87-94
Приложение № 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	95
Список использованной литературы . . . . . . . . . . . . . . . . . . . . . . . . . .	96

§1. Неопределенный интеграл

1.1. Основные понятия неопределенного интеграла

Неопределенным интегралом функции f(x) называется множество всех первообразных функций F(x) + C.

Записывается это так: ∫ f (x)dx = F(x) +C;

Первообразной функцией для функции f(x) на промежутке (a; b) называется такая функция F(x), производная которой равна f(x) на рассмат-

риваемом промежутке, то есть F ′(x) = f (x) .

Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.

Имеет место теорема: Две различные первообразные одной и той же функции, определенной в некотором промежутке, отличаются друг от друга в этом промежутке на некоторое постоянное слагаемое.

Функция f(x) называется непрерывной на отрезке [a, b], если 1) она определена на этом множестве; 2) непрерывна в каждой точке этого отрез-

ка, то есть x [a;b] справедливо равенство lim	y = lim[f (x + x) − f (x)]= 0 ,
x→0	x→0
где x + x [a;b] .

Теорема (условие существования неопределенного интеграла).

Всякая непрерывная на отрезке [a, b] функция имеет на этом промежутке неопределенный интеграл.

Основные теоремы (свойства неопределенного интеграла):

1.(∫ f (x)dx)′ = (F(x) +C)′ = f (x); где C-const.

2.d (∫ f (x)dx)= f (x)dx .

3.∫dF(x) = F(x) +C .

4.∫(u + v − w)dx = ∫udx + ∫vdx − ∫wdx; где u, v, w – некоторые функции от х.

5.∫C f (x)dx = C ∫ f (x)dx.

6. (Инвариантность формулы интегрирования). Если

∫ f (x)dx = F(x) +C , то и ∫ f (u)du = F(u) +C , где u =ϕ(x) - произвольная функ-

ция, имеющая непрерывную производную.

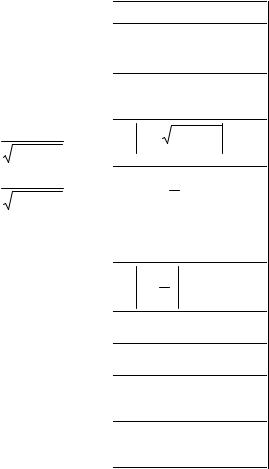
Ниже приводится таблица основных интегралов, которые используются при вычислениях неопределенных интегралов различных функций. Верность этой таблицы проверяется непосредственно дифференцированием.

Интеграл

Значение

Интеграл

∫xαdx

xα+1

+C,α ≠ −1

∫

a2 + x2

α +1

∫

x2 − a2

∫a

a x

∫

+ C

ln a

x2 ± a2

∫ex dx

ex + C

∫ a2dx− x2

∫sin(x)dx

− cos(x) + C

∫

cos(x)

∫cos(x)dx

sin(x) + C

∫

sin(x)

∫tg(x)dx

−ln

cos(x)

∫sh(x)dx

∫ctg(x)dx

sin(x)

∫ch(x)dx

∫

tg(x) + C

∫

cos2 (x)

sh2 (x)

∫

− ctg(x) + C

∫

sin 2 (x)

ch2 (x)

Таблица 1. Значение


1			x
	arctg				+C
a
			a
1			x − a		+C
		ln
2a			x + a

ln x +			x2	± a2 +C

arcsin ax +C

	x			π
ln	tg		+		+C
		2		4

ln tg 2x +C

ch(x) +C sh(x) +C

− cth(x) + C

th(x) + C

1.2. Основные методы интегрирования Метод непосредственного интегрирования

Метод интегрирования основан на применении табличных интегра-

лов, и называется непосредственным интегрированием. При этом дан-

ный интеграл может быть приведен к табличному с помощью тождествен-

ных преобразований подынтегральной функции и применения свойств неопределенного интеграла.

Примеры:

a) ∫(3x2

− 2sin(x) +5)dx = 3∫x2 dx − 2∫sin(x)dx +5∫dx = x3 + 2cos(x) +5x +C;

b) ∫

2 − x2 +

+ x2

2 − x2

+ 2 + x2

+ ∫

4 − x

dx = ∫

2 − x

2 + x

dx = ∫

2 + x

2 − x

= ln x +

+ 2

+C.

+ arcsin

с) ∫2x 32 x dx = ∫(2 32 )x dx = ∫18x dx =

18x

+C .

ln(18)

Замена переменной

Этот метод интегрирования основан на введении новой переменной интегрирования. Приведем пример: пусть дана сложная функция f(x), где x =ϕ(t) - функция имеющая непрерывную производную dx =ϕ′(t)dt . При-

меняется свойство инвариантности формулы интегрирования неопреде-

ленного интеграла, получаем: ∫ f (x)dx = ∫ f (ϕ(t))ϕ′(t)dt .

Эта формула называется формулой замены переменной в неопределенном интеграле.

Примеры:

ln (4 x + 5 )dx =

ln (4 x + 5 )= t 2

a) ∫

4 dx

= 2tdt

= ∫t

tdt =

∫t 2 dt

t 3

+ C =

ln 3 (4 x + 5)

+ C .

4 x + 5

= 1 tdt

4 x + 5

b) ∫

ex −1

= t 2 ,

ex = t 2 +1

= ∫

2tdt

= 2∫

= 2arctg(t) +C =

ex −1 =

x = ln(t 2

+1),

dx =

t(t 2

+1)

t 2

= 2arctg(

ex −1)+C .

с) ∫x(x2 +1)3 / 2 dx .

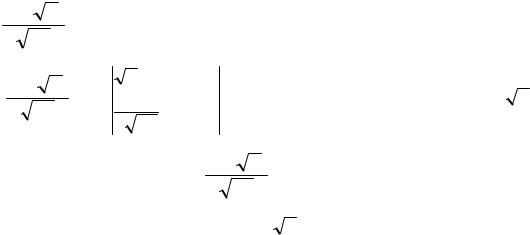
Первый вариант замены:

∫x(x2

+1)3 / 2 dx =

x 2 + 1 = t

= ∫t 3 / 2

∫t 3 / 2 dt =

5 / 2

+ C =

+1)

5 / 2

+ C.

2 xdx

= dt

xdx

Второй вариант замены:

∫x(x2

+1)3 / 2 dx =

x 2 + 1 = t 2

= ∫t

3tdt = ∫t 4 dt =

+C =

+1)

5 / 2

+C.

2 xdx

= 2 tdt

xdx

= tdt

d) ∫ sin3 (x3 2 x )dx . Первый вариант замены:

x = t

= −3 cos (3

x )+ C

∫

sin ( x )dx

∫

3 sin( t )dt

= −3 cos( t ) + C

3 x 2

33 x 2

Второй вариант замены: ∫

sin (3 x )

x = t 3

= ∫

3 sin( t )

dx = 3t

= ∫3 sin( t )dt

= −3 cos( t ) + C

= −3 cos (3

x )+ C .

При интегрировании заменой переменной важно удачно сделать подстановку. Однако нельзя дать общее правило выбора замены переменной для интегрирования любой функции. Это можно сделать только для интегрирования отдельных классов функций: рациональных, тригонометрических и т.д. (интегрирование этих классов функций предложены в таблицах

3 – 7).

Интегрирование по частям

Этот метод интегрирования основан на применении формулы дифференцирования произведения d(uv)=udv+vdu и вычислении затем интеграла

∫d (uv) = ∫udv + ∫vdu . Из этого равества получаем формулу интегрирова-

ния по частям: ∫udv = uv − ∫vdu .

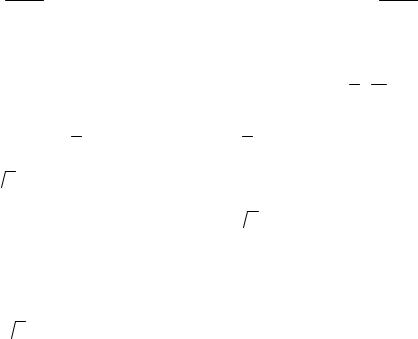
Примеры:

a) ∫(x2 −3x + 4)ex dx
Интегирируется по частям:	пусть u = x2 −3x + 4, dv = ex dx ;	тогда	v = ex ,
du = (2x −3)dx . Следовательно, ∫(x2 −3x +4)ex dx = (x2 −3x +4)ex		−∫(2x −3)ex dx.
Еще раз интегрируется по	частям: пусть u = 2x −3, dv = ex dx;		тогда

du = 2dx,v = ex . Получаем, ∫(x2 −3x + 4)ex dx = (x2 −3x + 4)ex −((2x −3)ex −

−∫2ex dx)= (x2 −3x + 4)ex −(2x −3)ex + 2ex +C .

b)∫xn ln(x)dx

Интегирируется

по

частям:

пусть

u = ln(x), dv = xn dx ;

тогда du =

v =

xn+1

. Следовательно, ∫xn ln(x)dx =

xn+1

ln(x) − ∫

xn+1

ln(x) −

n +1

n +1 x n +1

xn+1

−

∫xn dx =

ln(x) −

+C .

n +1

(n +1)2

c) ∫arctg(x)dx

Интегирируется

по

частям:

пусть

u = arctg(x), dv = dx ; тогда v = x ,

du = 1+dxx2 . Следовательно, ∫arctg(x)dx = x arctg(x) − ∫1x+dxx2 .

Получившийся интеграл вычисляется методом замены переменной:

1+ x2 = t, 2xdx = dt . Тогда ∫arctg(x)dx = x arctg(x) − 12 ∫dtt =

=x arctg(x) − 12 ln(t) +C = x aectg(x) − 12 ln(1+ x2 )+C .

d)∫sin( x )dx

Пусть x = t 2 , dx = 2tdt . Тогда ∫sin( x )dx = ∫2t sin(t)dt = 2∫t sin(t)dt .

Интегирируется по частям: пусть u = t, dv = sin(t)dt ; тогда du = dt,

v= −cos(t) . Следовательно,

∫sin( x )dx = 2(−t cos(t) + ∫cos(t)dt)= −2t cos(t) + 2sin(t) +C =

=−2 x cos( x )+ 2sin( x )+C .

e)∫ a2 − x2 dx

Интегирируется по частям: пусть u = a2 − x2 , dv = dx ; тогда

du = −

xdx

, v = x . Следовательно,

a2 − x2

∫

− x

dx = x a

− x

− ∫

− x x dx

= x a

− x

− ∫

a2 − x2 + a

dx =

− x

= x

− x

∫

a2 − x2

dx − a

∫

= x

− x

− ∫

− x

dx − a

−

− x

arcsin

Обозначается,

∫

− x

= I

. Тогда I = x

− x

− I

− a

arcsin

Следовательно,

∫

− x

dx =

− x

−

+C .

arcsin

f) ∫x arcsin(x)dx

Интегирируется по частям: пусть u = arcsin(x), dv = xdx ; тогда du = dx

1− x2

v =

. Следовательно,

∫x arcsin(x)dx

arcsin(x) − ∫

x2 dx

1− x

1 1− x2 −1

1− x2

arcsin(x) +

∫

dx =

arcsin(x) +

∫

dx −

∫

1− x

− x

arcsin(x) +

(

1− x

dx −arcsin x)=

arcsin(x)

1− x

arcsin(x)

−

∫

−arcsin(x))+C =

(2x2 arcsin(x) + x

1− x2

− 2arcsin(x))+C .

g) ∫e2 x cos(x)dx

Интегрируется по частям: пусть u = e2 x , dv = cos(x)dx;

тогда du = 2e2 x dx,

v = sin(x) . Следовательно, ∫e2 x cos(x)dx = e2 x sin(x) − ∫sin(x) 2e2 x dx .

Еще раз интегрируется по частям: пусть u = e2x , dv = sin(x)dx; тогда

du = 2e2 x dx, v = −cos(x) . Получается,

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
14.02.2015202.24 Кб28mol.doc
#
25.11.2019282.31 Кб4MOTIVATION THEORIES.docx
#
14.02.201581.2 Кб5moy_otchet_Avtosokhranenny.docx
#
12.03.2016930.75 Кб33moy_otchyot_po_vinu.docx
#
14.02.20151.69 Mб4nalogovyy-kodekss-chast-1.doc
#
14.02.20151.18 Mб17neopred_int(математика).pdf
#
31.07.201944.54 Кб3nReferat.ru - Metodika Obucheniya Barernomu Beg....doc
#
14.02.20151.1 Mб10nwpi221.pdf
#
14.02.20151.14 Mб43O.A.Platonov-Russkaya_pravda.pdf
#
14.02.2015408.06 Кб357obraztsi_dokumentov_proc_docs.doc
#
14.02.2015838.66 Кб79oeppp088.doc