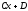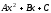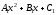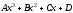- •Методические указания
- •Общие методические указания
- •Примеры решения задач
- •Тема 1. Элементы аналитической геометрии на плоскости
- •Тема 2. Элементы линейной алгебры
- •Тема 3. Основы векторной алгебры
- •Вычислить длину вектора , если,,,.
- •Тема 4. Введение в математический анализ
- •Тема 5. Производная и дифференциал Правила дифференцирования:
- •Тема 6. Исследование поведения функции
- •Тема 7. Неопределенный интеграл
- •Тема 8. Определенный интеграл
- •Тема 9. Приложения определенного интеграла
- •Тема 10. Функции нескольких переменных
- •Тема 11. Кратные интегралы.
- •Тема 12. Ряды
- •Тема 13. Дифференциальные уравнения первого порядка
- •Тема 14. Дифференциальные уравнения второго порядка
- •Тема 15. Основы теории вероятностей
- •Тема 16. Элементы математической статистики
- •Контрольные задания для студентов - заочников экономического факультета
- •Контрольная работа №1
- •Тема: «линейная алгебра»
- •Тема: «аналитическая геометрия (прямая на плоскости)»
- •Тема: «элементы векторной алгебры»
- •Тема: «функции 2-х переменных»
- •Контрольная работа №2
- •Тема: «случайные величины»
- •Контрольные задания для студентов - заочников агрономического факультета
- •Контрольная работа 1.
- •Контрольная работа 2.
- •Контрольные задания для студентов - заочников биолого-технологического факультета и факультета ветеринарной медицины
- •Контрольные задания для студентов - заочников инженерного факультета и института природообустройства
- •Приложение
- •Литература
- •Содержание
При составлении частного решения
 удобно использовать следующую таблицу:
удобно использовать следующую таблицу:Степень многочлена
Вид многочлена
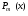
Вид многочлена
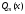
 =0
=0
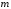 =1
=1
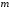 =2
=2
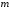 =3
=3
Решение:
а)
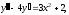
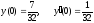 .
.Общее решение данного уравнения имеет вид:
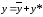 .
.Найдём
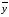 .
Для этого решим соответствующее
однородное уравнение
.
Для этого решим соответствующее
однородное уравнение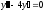 .
Составляем характеристическое уравнение:
.
Составляем характеристическое уравнение: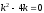 .
Корнями этого уравнения являются
.
Корнями этого уравнения являются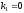 и
и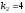 .
Т.к. решения действительные различные
числа (первый случай), то
.
Т.к. решения действительные различные
числа (первый случай), то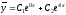 или
или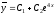 .
.Теперь найдём
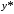 .
Правая часть
.
Правая часть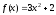 имеет специальный вид, причём
имеет специальный вид, причём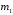 =2,
=2,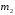 =0,
значит
=0,
значит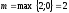 ,
, =0,
=0, =0,
тогда
=0,
тогда
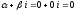 и
и
 ,
т.о.
,
т.о.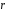 =1.
=1.Получаем:
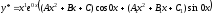 ,
т.к.
,
т.к.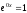 ,
,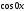 =1,
=1,
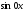 =0,
то
=0,
то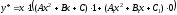 ,
,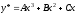 .
Найдём производные первого и второго
порядка от
.
Найдём производные первого и второго
порядка от
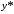 .
.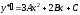 ,
,
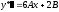 .
Запишем
.
Запишем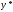 ,
,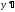 и
и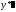 следующим образом, подписывая слева
коэффициенты
следующим образом, подписывая слева
коэффициенты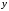 ,
, и
и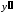 из
исходного уравнения:
из
исходного уравнения: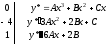
Далее приравниваем коэффициенты при соответствующих степенях
 :
: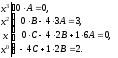

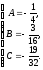
Тогда
 .
Следовательно, общее решение исходного
уравнения:
.
Следовательно, общее решение исходного
уравнения:
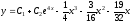 .
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
.
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём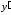 :
: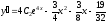 .
.Подставляем начальные условия
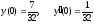 в
в
 и
и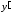 .
.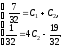 Отсюда
Отсюда
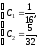
Тогда
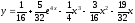 -частное
решение исходного уравнения.
-частное
решение исходного уравнения.б)
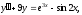
Общее решение данного уравнения имеет вид:
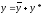 .
.Найдём
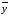 .
Для этого решим соответствующее
однородное уравнение
.
Для этого решим соответствующее
однородное уравнение .
Составляем характеристическое уравнение:
.
Составляем характеристическое уравнение: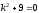 ,
,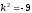 .
Корнями этого уравнения являются
.
Корнями этого уравнения являются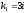 и
и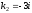 .
Т.к. решения комплексные числа (третий
случай), то
.
Т.к. решения комплексные числа (третий
случай), то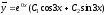 или
или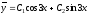 .
.Теперь найдём
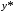 .
Правая часть
.
Правая часть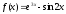 есть сумма двух функций, имеющих
специальный вид:
есть сумма двух функций, имеющих
специальный вид: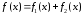 ,
где
,
где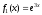 и
и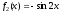 .
Тогда
.
Тогда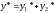 .
.Рассмотрим
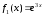 .
Имеем
.
Имеем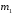 =0,
=0,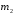 =0,
значит
=0,
значит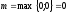 ,
, =3,
=3,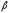 =0,
тогда
=0,
тогда
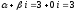 не совпадает ни с одним из корней
характеристического уравнения, т.о.
не совпадает ни с одним из корней
характеристического уравнения, т.о.
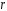 =0.
=0.Получаем:
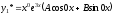 ,
т.к.
,
т.к.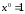 ,
,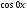 =1,
=1,
 =0,
то
=0,
то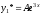 .
.Рассмотрим
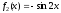 .
Имеем
.
Имеем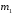 =0,
=0,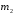 =0,
значит
=0,
значит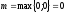 ,
, =0,
=0,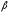 =2,
тогда
=2,
тогда
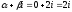 не совпадает ни с одним из корней
характеристического уравнения, т.о.
не совпадает ни с одним из корней
характеристического уравнения, т.о.
 =0.
=0.Получаем:
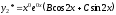 ,
т.к.
,
т.к.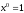 ,
,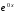 =1,
то
=1,
то
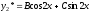 .
.Тогда
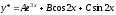 .
Найдём производные первого и второго
порядка от
.
Найдём производные первого и второго
порядка от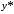 .
.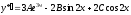 ,
,
 .
Запишем
.
Запишем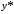 ,
,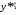 и
и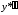 следующим образом, подписывая слева
коэффициенты
следующим образом, подписывая слева
коэффициенты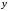 ,
,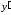 и
и из
исходного уравнения:
из
исходного уравнения: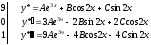
Далее приравниваем коэффициенты при соответствующих подобных слагаемых:


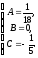
Тогда
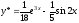 .
Следовательно, общее решение исходного
уравнения:
.
Следовательно, общее решение исходного
уравнения:
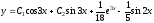 .
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём
.
Чтобы найти частное решение, удовлетворяющее
начальным условиям, найдём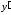 :
: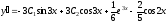 .
Подставляем начальные условия
.
Подставляем начальные условия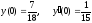 в
в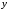 и
и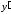 .
.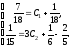 Отсюда
Отсюда
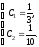
Тогда
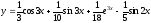 -
частное решение исходного уравнения.
-
частное решение исходного уравнения.Тема 15. Основы теории вероятностей
Задача 32.
В партии из 10 деталей 7 стандартных. Какова вероятность того, что из 6 взятых наугад деталей 4 стандартные.
Решение:
Используем классическое определение вероятности
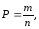
где
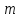 - число благоприятных (благоприятствующих)
исходов,
- число благоприятных (благоприятствующих)
исходов,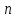 - общее число исходов. Тогда
- общее число исходов. Тогда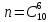 - число способов выбрать 6 деталей из
10 (число сочетаний
- число способов выбрать 6 деталей из
10 (число сочетаний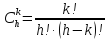 ,
,
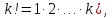
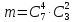 - число способов
выбрать 4 стандартные детали из 7 и 2
нестандартные из 3. Получаем
- число способов
выбрать 4 стандартные детали из 7 и 2
нестандартные из 3. Получаем
 .
.Основные свойства вероятности.
Вероятность невозможного события равна нулю.
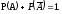
Для любого события А
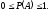
Условной вероятностью события А при условии В называется вероятность события А, найденная при условии, что событие В уже произошло.
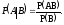
Правило умножения вероятностей.
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло.
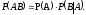
Два события называются независимыми, если появление одного из них не меняет вероятности появления другого.
Для независимых событий правило умножения принимает вид:
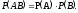
Правило сложения вероятностей.
Вероятность суммы двух совместных событий есть сумма их вероятностей минус вероятность их произведения.
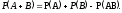
Для несовместных событий правило сложения принимает вид:
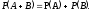
Формула полной вероятности.
Пусть событие А может произойти только с одним из событий H1, H2, …, Hn, образующих полную группу попарно несовместных событий, т.е.
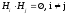 и
и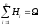 .
Тогда вероятность события А вычисляется
по формуле полной вероятности:
.
Тогда вероятность события А вычисляется
по формуле полной вероятности: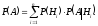
События H1, H2, …, Hn называют гипотезами, а числа
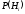 - вероятностями гипотез.
- вероятностями гипотез.Формула Байеса.
Если в результате опыта осуществилось событие А, то прежние доопытные или априорные вероятности гипотез
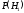 ,
…,
,
…, должны быть заменены на новые, послеопытные
или апостериорные вероятности, которые
вычисляются по формуле Бейеса:
должны быть заменены на новые, послеопытные
или апостериорные вероятности, которые
вычисляются по формуле Бейеса: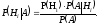
Вероятность P(A) вычисляется по формуле полной вероятности.
Задача 33.
Из ящика, в котором 6 белых и 4 черных шара, наугад 3 раза извлекают шар. Извлеченный шар обратно не возвращают. Какова вероятность того, что все 3 извлеченных шара белые.
Решение:
Пусть событие
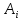 состоит в том, чтоi-й
шар белый, i=1,
2, 3. События зависимы, так как количество
шаров после каждого извлечения меняется.
Используем правило умножения вероятностей,
получим
состоит в том, чтоi-й
шар белый, i=1,
2, 3. События зависимы, так как количество
шаров после каждого извлечения меняется.
Используем правило умножения вероятностей,
получим 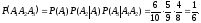
Задача 34.
Всхожесть семян данного растения составляет 90 %. Какова вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее четырех.
Решение:
Воспользуемся формулой Бернулли. Если производится п независимых испытаний, при каждом из которых вероятность осуществления событий А постоянна и равна р, а вероятность противоположного события q=1-р, то вероятность Рп(т) того, что при этом событие А осуществляется ровно m раз, вычисляется по формуле:
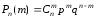 ,
(1)
,
(1) 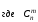 –есть
число сочетаний из п
элементов
по т.
–есть
число сочетаний из п
элементов
по т.а) По условию задачи вероятность всхожести семян р=0,9; тогда q= 0,1; в данном случае n=5 и т = 4. Подставляя эти данные в формулу Бернулли (1), получим
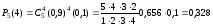 .
.б) Искомое событие А состоит в том, что из пяти посеянных семян взойдут или четыре, или пять. Таким образом,
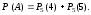 Первое
слагаемое уже найдено.
Для вычисления второго снова применяем
формулу
(1):
Первое
слагаемое уже найдено.
Для вычисления второго снова применяем
формулу
(1):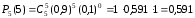 .
.Следовательно, Р(А) =0,328 +0,591 = 0,919.
Задача 35.
Предположим, что 5% всех мужчин и 0,25% всех женщин дальтоники. Число мужчин и женщин считать одинаковым. 1) Какова вероятность того, что наугад выбранный человек оказался дальтоником? 2) Наугад выбранный человек оказался дальтоником. Какова вероятность, что это мужчина?
Решение:
Пусть событие A={случайно выбранный человек – дальтоник}. Введем гипотезы: H1={случайно выбранный человек – мужчина}, H2={случайно выбранный человек – женщина}.
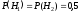 ,
,
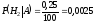 .
.
По формуле полной вероятности определим
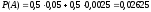 .
.
По формуле Байеса имеем