7. Задачи аппроксимации функций (интерполяция, экстраполяция, приближение в среднем). Способы построения интерполяционного полинома. Аппроксимации на основе ортогональных базисов. Понятие сплайна.

Задачи аппроксимации функций. Интерполяция – это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Экстраполяция – процесс оценки значения за пределами диапазона известных значений.

Экстраполяция опирается на предположения о поведении данных за пределами известного диапазона. Другими словами, интерполяция используется для оценки значений между известными точками данных, а экстраполяция - для оценки значений за пределами известных точек данных.

Приближение в среднем – вероятно, является обобщением для целого класса аппроксимирующих функций, когда предположение о новом неизвестном значении наблюдения, лежащего в указанном диапазоне, определяется как значение аппроксимирующей функции, проходящей между узлов интерполяции.

Отличие интерполяционного многочлена от аппроксимирующей функции в том, что интерполяционная функция имеет те же значения в узлах интерполяции, что и фактически наблюдаемые в ходе реального эксперимента (рис. а), в то время как аппроксимирующая функция является лишь приближенной функциональной зависимостью, иногда говорят, эмпирической формулой (рис. б) Аппроксимирующие функции проще формулируются и выглядят сглажено, т.к. имеют меньшее число коэффициентов.

Способы построения интерполяционного полинома. Интерполирующую функцию ищут в виде полинома степени . Для каждого набора экспериментальных точек имеется только один интерполяционный многочлен, степени не больше . Рассмотрим канонический полином и интерполяционные многочлены Ньютона и Лагранжа.

Запишем вид канонического полинома степени в общем виде:

Выбор многочлена степени основан на том факте, что через точку проходит единственная кривая степени . Составим систему линейных алгебраических уравнений, в котором каждой точке соответствует :

Решая эту систему линейных алгебраических уравнений, найдем коэффициенты интерполяционного полинома , , … .

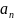Интерполяция полиномом Лагранжа имеет вид, где – множитель Лагранжа:

Интерполяционный многочлен Ньютона имеет несколько форм, но для примера мы воспользуемся только одним из них.

Первый интерполирующий полином Ньютона записывается в виде:

Исходя из того, что в узлах интерполяции, наблюдаемое табличное значение и результат вычисления полинома совпадают, получим формулу для нахождения первого коэффициента :

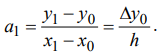
Обобщенная формула для нахождения всех коэффициентов имеет вид:

Тогда исходная формула принимает следующий вид:

Аппроксимации на основе ортогональных базисов. Ортогональная интерполяция – это тип метода интерполяции, который использует ортогональные полиномы¹ для оценки неизвестных значений между известными точками данных.

Ортогональная интерполяция имеет ряд преимуществ перед другими методами интерполяции. Она эффективна с вычислительной точки зрения, может обрабатывать большие наборы данных и дает точные результаты даже при наличии шума или неравномерного распределения данных. Кроме того, ее можно расширить до более высоких измерений для интерполяции многомерных данных.

Примерами ортогональных базисных функций являются полиномы Лежандра, Чебышева и ряды Фурье.

Полиномы Лежандра – это набор полиномов, ортогональных интервале [-1;1], относительно своей весовой функции . Таким образом внутреннее произведение² любых двух различных полиномов Лежандра равно нулю. Первые несколько полиномов Лежандра следующие:

Чтобы использовать полиномы Лежандра, необходимо определить степень аппроксимации полинома, от этого будет зависеть сложность функции и то, насколько точно будут аппроксимированы данные.

Определив степень полиномиального приближения, следует вычислить коэффициенты разложения полинома Лежандра с помощью метода наименьших квадратов. Это даст набор коэффициентов, которые можно использовать для построения аппроксимации полиномом Лежандра.

Понятие сплайна. В аппроксимации сплайн – это кусочно-определенная функция, которая строится путем подгонки полиномиальных сегментов гладким и непрерывным образом. Сплайны часто используются для аппроксимации сложных кривых или поверхностей и могут обеспечить более гибкое и точное представление, чем более простые методы интерполяции, такие как линейная или полиномиальная интерполяция.

¹Ортогональные полиномы или ортогональные базисные функции, определены на интервале с некоторой ненулевой весовой функцией так, что их внутренне произведение равно нулю. Аналогично ортогональным векторам, образующим базис пространства.

²Внутреннее произведение двух функций и на интервале [a, b] определяется как: . Весовую функцию используют, чтобы придать большее и меньшее значение определенным частям интервала. Внутреннее произведение показывает степень сходства между двумя функциями, основываясь на площади по кривой двух функций на заданном интервале. Аналогично скалярному произведению векторов.