4. Производные. Необходимое и достаточное условие дифференцируемости функции. Частные производные. Полный дифференциал. Производная и дифференциал сложной функции.

Производные. Производная по определению является пределом отношения приращения функция к приращению ее аргумента, при стремлении последнего к нулю.

Геометрический смысл производной в точке можно передать в качестве углового коэффициента касательной к функции в этой точке.

Касательная в точке M же может быть определена как секущая MM₁ при условии, что M₁ неограниченно приближается к M, переходя в касательную. Отсюда также следует, что и угол приближается к значению угла .

Физический смысл производной может варьироваться в зависимости от области науки, в которой применяется, но в общем отражает скорость протекания физического или химического процесса, силу тока, линейную плотность стержня и т.д.

Достаточное условие дифференцируемости. Функция , имеющая производную в каждой точке интервала, называется дифференцируемой на этом интервале, а операция нахождения производной функции называется дифференцированием. Верно и то, что если функция дифференцируема в точке, то она непрерывна в ней.

Частные производные. Если функция имеет несколько аргументов, то можно ввести понятие частной производной, т.е. производной этой функции по одному из ее аргументов. Это значит, что при вычислении производной, один из ее аргументов будет зафиксированной константой, а другой – изменяющейся величиной. Обозначается как или, аналогично, . Иногда, можно встретить такой цельный символ: « », но не стоит путать его с математическим выражением отношения дифференциала функции одной переменной к дифференциалу ее аргумента – . При этом по определению производной: , где – частный дифференциал функции по x, – дифференциал аргумента, а – частная производная функции по x. Дифференциалом, в свою очередь, называют линейную часть приращения функции или ее аргумента. В общем случае для функции вида , и не равны, как и показано на рисунке ниже, но при стремлении N к M разница между ними сокращается до пренебрежительно малой величины.

Полный дифференциал. Полным дифференциалом функции будет сумма ее дифференциалов по всем аргументам: .

Производная и дифференциал сложной функции.

При этом дифференциал сложной функции сохранит свой вид, вне зависимости от того, является ли ее аргумент независимой переменной или же другой функцией. Положим, что есть некоторая функция 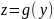, дифференциал которой выглядит следующим образом: . Если предположить, что в свою очередь является функцией вида , для которой справедливо выражение , то дифференциал сложной функции сохранит свой прежний вид: . Это свойство принято называть инвариантностью формы первого дифференциала.

5. Градиент функции. Производные по направлению. Необходимые и достаточные условия экстремума функции многих переменных. Условные экстремумы. Метод множителей Лагранжа.

Градиент функции. Вектор, координатами которого являются значения частных производных функции в точке называют градиентом функции и обозначают или через оператор набла .

Градиент описывает направление наикротчайшего изменения функции, его модуль равен максимальной скорости изменения функции.

Производная по направлению.

Производной от функции 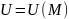в точке по направлению называется предел вида:

Выведем формулу для вычисления производной по направлению, считая, что функция дифференцируема в точке M.

Учитывая, что , , – бесконечно малые величины при переходе к пределу , получим формулу для вычисления производной по направлению:

Производная по направлению характеризует скорость изменения функции в точке по этому направлению, а ее модуль отражает значение мгновенной скорости этой функции.

Градиент и производная по направлению могут быть связаны через единичный вектор , где – направляющие косинусы.

Таким образом, для вычисления производной скалярной функции векторного аргумента по любому направлению достаточно знать градиент функции, то есть вектор, компоненты которого являются её частными производными.

Необходимые и достаточные условия экстремума функции многих переменных. Необходимым условием экстремума функции является равенство нулю всего его первых частных производных. Точки, для которых частные производные равны нулю называются стационарными точками. Иногда говорят точки «подозрительные» на экстремум, однако, это не всегда так. Например, седловая точка тоже имеет равными нулю все частные производные первого порядка, но не является экстремумом.

Достаточное условие говорит, что если квадратичная форма, составленная из вторых производных функции, вычисленных в стационарной точке, определена, то в этой точке функция имеет минимум, если квадратичная форма положительно определена, и наоборот. Если знак определить нельзя, то точка не является экстремумом. Для определения знака используется критерий Сильвестра, который требует, чтобы все угловые миноры квадратичной матрицы были больше нуля.

Условные экстремумы. Исходя из названия, условные экстремумы это значения, которые исследуемая функция принимает, при некотором условии. Условие может быть задано уравнением, которое принято называть уравнением связи.

Метод множителей Лагранжа. Например, может потребоваться вычислить минимум функции при условии, что .

Для решения описанной задачи через метод множителей Лагранжа необходимо составить уравнение вида: , где – так называемый множитель Лагранжа. Перепишем уравнение, подставив наши значения: .

Следующим шагом идет взятие частных производных и составление системы уравнений вида:

В результате решением системы линейных уравнений получим и . Подставив полученные значения в уравнение связи найдем число Лагранжа, . Таким образом мы получили две стационарные точки, подозрительные на экстремум и . Далее применяем операцию дифференцирования для нахождения производных второго порядка и обосновываем, что полученные стационарные точки действительно являются экстремумами функции при условии .

6. Неопределенный и определенный интеграл, методы их вычисления. Теорема о среднем и ее практический смысл. Виды многомерных интегралов (по объему, по поверхности, и пр.). Теорема Гаусса-Остроградского.

Неопределенный и определенный интеграл, методы их вычисления. Интегральное исчисление решает задачу обратную дифференцированию, т.е. задачу нахождения первообразной по ее производной.

Множество всех первообразных функции для функции называется неопределенным интегралом от функции и обозначается символом . Таким образом по определению:

Определенный интеграл от той же функции на области (отрезке) интегрирования 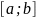обозначается: .

Наиболее широко используемым видом определенного интеграла является интеграл Римана. Он предложил описать процесс интегрирования как взятие предела интегральной суммы произведения длин частичных отрезков функции , определённой на некотором интервале , на значения этой функции в произвольной точке соответствующего ей частичного отрезка .

Таким образом, определенный интеграл Римана задается выражением:

В литературе и на практике часто упоминается обобщенный вариант интеграла Римана на более широкий класс функций, получивший название интеграла Лебега.

Определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции. В этом состоит его геометрический смысл.

Для вычисления определенного интеграла можно воспользоваться соответствующей формулой Ньютона-Лейбница:

В общем случае, для вычисления интегралов справедливо следующее:

1. Подведение под знак интеграла;

2. Интегрирование подстановкой (заменой переменной);

3. Интегрирование по частям;

Рассмотрим методы интегрирования рациональных функций. Так, при интегрировании рациональных дробей следует использовать следующий алгоритм:

1. Если дробь неправильна, ее необходимо представить в виде суммы многочлена и правильной дроби;

2. Затем знаменатель правильной рациональной дроби необходимо разложить на множители, представив таким образом дробь в виде суммы простейших рациональных дробей;

3. Проинтегрировать многочлен и полученную сумму простейших дробей по правилам, описанным ранее, в соответствии с таблицей основных интегралов.

При интегрировании тригонометрических функций необходимо воспользоваться тригонометрической универсальной подстановкой:

Впрочем, возможно и использование известных тригонометрических преобразований:

Следующий большой класс функций составляют иррациональные функции. Квадратичные иррациональности представляют собой интегралы вида:

Для их решения следует попробовать выделить под корнем полный квадрат:

И затем сделать подстановку , при этом интегралы сводятся к табличным.

Следующий вид иррациональных функций, по сути, представляет собой те же дробные функции, но с корнями степеней:

Вычисляются через добро-линейную подстановку, где – наименьшее общее кратное знаменателей дробей :

Последний рассматриваемый вид иррациональных функций представляет собой следующие интегралы:

Решается благодаря тригонометрическим подстановкам, вот несколько примеров, соответствующих приведенным выше задачам: , , .

Теорема о среднем и ее практический смысл. Если функция непрерывна на отрезке , то существует точка такая, что:

Применяя к интегралу формулу Ньютона-Лейбница, получим выражение, соответствующее теореме Лагранжа о конечном приращении функции:

Теорема о среднем, при имеет простой геометрический смысл: значение определенного интеграла равно, при некотором , площади прямоугольника с высотой и основанием .

Число называется средним значением функции на отрезке .

Виды многомерных интегралов.

Двойной интеграл. Представляет собой обобщение определенного интеграла на случай функции двух переменных.

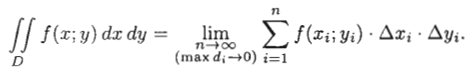
Геометрический смысл двойного интеграла – это площадь плоской фигуры, а также объём цилиндрического тела, в области ограниченного некоторой поверхностью .

Тройной интеграл. Представляет собой обобщение определенного интеграла на случай функции трех переменных.

Геометрический смысл тройного интеграла – это объем произвольной трехмерной фигуры.

Криволинейный интеграл 1-ого рода. Представляет собой обобщение определенного интеграла на случай, когда область интегрирования есть некоторая кривая.

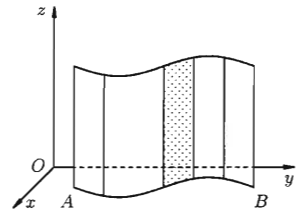
Геометрический смысл криволинейного интеграла можно интерпретировать и как длину кривой, и как площадь цилиндрической поверхности.

Криволинейный интеграл 2-ого рода. Определяется почти также как криволинейный интеграл 1-ого рода, но на случай нескольких кривых.

Криволинейный интеграл от функции по координате выражается как:

Криволинейный интеграл от функции по координате выражается как:

Криволинейный интеграл 2-ого рода общего вида задаётся выражением:

Поверхностный интеграл 1-ого рода. Представляет собой обобщение двойного интеграла.

Поверхностный интеграл 2-ого рода. Строится по образцу криволинейного интеграла 2-ого рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.

Теорема Гаусса-Остроградского. Формула устанавливает связь между поверхностным интегралом 2-ого рода по замкнутой поверхности и тройным интегралом по объёму, ограниченному этой поверхностью.