Величина/закон
Теорема ОстроградскогоГаусса, теорема о циркуляции
Энергетическая
характеристика
Связь между энергетической и силовой характеристиками
Момент
Момент силы
Энергия
Силовая
характеристика поля в веществе
Вспомогательная
силовая
характеристика
240
Электрическое поле
Теорема о циркуляции E :
Теорема Остроградского-
Гаусса для E |
: |
|
|
|
|
|
q |
S , |
divE |
ρ |
EdS |
|
ε |
|
|
ε |
S |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
Потенциал φ: |
|
|
|
φ |
|
|
A |
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
E φ , |
|
φ12 |
|
|
Edl |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
ρ |
|
|
|
|
φ |
ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Дипольный момент |
|
|
|
p |
|
ql |
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
M |
p ,E |
|
|
|
|
|
|
|
e |
|
|
|
|
Энергия диполя
W pe E
Поляризованность
P pe V
Электрическое смещение
D ε0 E P
Таблица 29.2 (продолжение)
Магнитное поле
Теорема ОстроградскогоГаусса для B :
|
|
divB 0 |
|
|
|
BdS 0 , |
|
|
|
S |
|
|
|
|
Теорема о циркуляции B |
: |
|
0 |
|
|
0 |
|
|
Bdl μ I |
L |
, rot B |
μ |
j |
|
|
|
|
|
L |
|
|
|
|
|
Векторный потенциал |
A |
: |
|
rot A B , div A 0 |
|
|
|
Магнитный поток74 |
|
|
|
Φ BdS |
|
|
|
S |
|
|
|
|
Магнитный момент pm ISn
Энергия контура с током
Намагниченность
J pm V
Напряжённость магнитного поля
74 Эта величина не является энергетической характеристикой магнитного поля. Она приведена в этой ячейке ТАБЛ. 29.2, так как занимает в некоторых формулах, относящимся к проводникам с током, место, аналогичное тому, что занимает потенциал (разность потенциалов) или заряд в формулах, описывающих заряженные проводники.
243
Лекция 30
3.13. Электромагнитные колебания
В электрической цепи, содержащей конденсатор и катушку индуктивности (или проводники, обладающие отличными от нуля ёмкостью и индуктивностью) — колебательном контуре, — могут возникать электромагнитные колебания. Если сообщить конденсатору заряд и замкнуть цепь, то конденсатор будет разряжаться через катушку. По катушке будет идти переменный ток, который по закону электромагнитной индукции будет создавать в катушке индуцированное электрическое поле, препятствующее изменению тока. Конденсатор будет разряжаться и перезаряжаться, а ток в цепи расти, убывать и менять направление: заряд конденсатора и ток в цепи будут изменяться периодически, т. е. будут происходить элек-
тромагнитные колебания.
3.13.1. Свободные незатухающие колебания (R = 0)
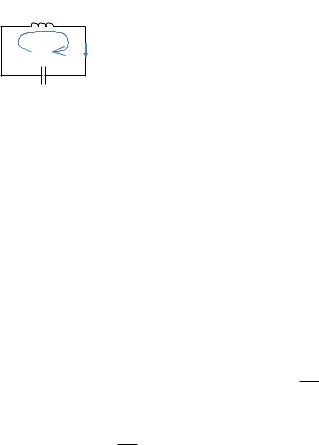
Схема электрической цепи, в которой происходят свободные незатухающие электромагнитные колебания, представлена на РИС. 30.1. Так как сопротивление цепи равно нулю, ток будет изменяться по модулю и направлению, а конденсатор перезаряжаться неограниченно долго — возникнут свободные незатухающие электромагнитные колебания.
L |
|
Обобщённый закон Ома для контура 12 (1 и 2 — обкладки конден- |
|
сатора) |
|
|
|
|
1 |
I |
φ1 φ2 Es 0, |
(30.1) |
2 |
Es — ЭДС самоиндукции — единственная ЭДС в этой цепи. Раз- |
C |
|
|
ность потенциалов между обкладками конденсатора |
по закону электромагнитной индукции
|
|
|
|
Es L |
dI |
. |
|
|
|
|
dt |
|
|
|
|
|
|
|
По определению силы тока |
I |
dq |
(здесь знак |
|
dt |
|
|
|
|
|
|
|
|
(30.3)
«–» обусловлен тем, что при раз-
рядке конденсатора его заряд уменьшается). Подставив это выражение, а также
(30.2) и (30.3) в уравнение (30.1):
|
q |
|
|
|
2 |
|
|
L |
d q |
|
C |
|
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
q |
|
d q |
|
|
dt |
2 |
LC |
|
|
|
|
|
Это дифференциальное уравнение свободных гармонических колебаний (см. 1.14.2).
2 |
|
1 |
, запишем его в стандартном виде (15.1) |
Обозначив ω0 |
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2q |
ω2q 0 |
. |
|
|
|
|
dt2 |
0 |
|
Общее решение этого уравнения
A и φ — постоянные интегрирования, которые находятся из начальных условий.
Собственная циклическая частота колебательного контура
период свободных незатухающих электромагнитных колебаний
|
T0 |
2π |
2π |
LC . |
|
ω |
|
|
|
|
|
|
|
|
0 |
|
|
|
Зависимость тока от времени |
|
|
|
|
|
I t |
dq |
Aω sin ω t |
|
|
|
|
dt |
|
0 |
0 |
|
|
|
|
|
Пусть в начальный момент времени заряд конденсатора равен q0, а тока в цепи нет. Подставим начальные условия в общее решение (30.4) и формулу (30.5):
Напряжение на конденсаторе
|
|
|
|
q A, |
|
q |
Acosφ, |
0 |
0 |
|
|
|
0 Aω0 sinφ |
φ 0; |
q t q cosω t , |
|
|
|
0 |
0 |
|
|
I t qω sinω t. |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
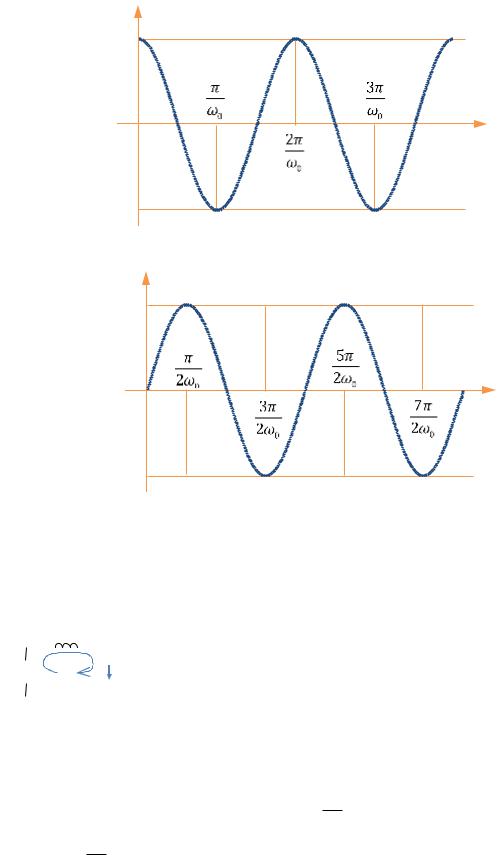
Графики зависимостей q(t) и I(t) при указанных начальных условиях показаны на РИС. 30.2А, Б. Видно, что ток опережает заряд конденсатора (и напряжение на кон-
Энергия электромагнитного поля в колебательном контуре (энергия колебательного контура) складывается из энергии электрического поля конденсатора и энергии магнитного поля катушки:
|
2 |
|
LI |
2 |
|
2 |
|
LI |
2 |
W |
q |
|
|
|
q |
|
|
|
|
|
m |
|
m |
|
|
|
|
|
|
|
|
|
2C |
|
2 |
|
2C |
|
2 |
где qm, Im — соответственно амплитуды заряда конденсатора и тока в цепи. Студенты доказывают утверждение (30.6) самостоятельно.
245
q q0
–q0
а
I
q0ω0
–q0ω0
б
Рис. 30.2
3.13.2. Свободные затухающие колебания
Пусть теперь электрическое сопротивление цепи отлично от нуля (см. схему на РИС. 30.3, содержащую элемент R).
|
|
|
|
L |
|
|
|
Обобщённый закон Ома для участка цепи 12: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
I |
|
|
|
|
φ1 φ2 Es IR . (30.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставим в это уравнение выражения (30.2) и (30.3): |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
q |
L |
dI |
IR . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 30.3 |
|
Учитывая, что |
I |
dq |
, запишем это уравнение как |
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
R dq |
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
d q |
|
|
0 |
; |
|
|
|
|
|
|
|
|
|
|
|
dt |
2 |
L dt |
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обозначим LC1 ω02 , RL 2β , где β — коэффициент затухания; получим уравнение
(16.1)
246
2 |
|
|
dq |
|
|
d q |
2β |
2 |
|
|
2 |
|
ω q 0 |
(30.8) |
dt |
|
dt |
0 |
|
|
|
|
— дифференциальное уравнение свободных затухающих колебаний (см. 1.14.3). Это однородное дифференциальное уравнение второго порядка с постоянными коэф-
фициентами. Его характеристическое уравнение
Эти корни могут быть как действительными, так и комплексными. Общее решение дифференциального уравнения (30.8)
|
|
|
|
|
|
|
q t A1e |
λ t |
A2e |
λ t |
, |
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 и A2 — постоянные интегрирования. |
|
|
|
|
|
|
1. Сильное затухание (β ≥ ω0) |
|
|
|
|
|
|
|
|
|
|
|
Корни характеристического уравнения (30.9) — |
q |
действительные. Общее решение дифференци- |
|
ального уравнения (30.8) |
|
|
|
|
|
|
|
|
|
|
|
q0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
β |
2 |
2 |
t |
|
|
β |
2 |
2 |
t |
|
|
|
|
|
q t A e |
|
β |
ω |
A e |
|
β |
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
— апериодическое решение (разрядка конденса- |
|
тора). График этого |
решения представлен |
на |
|
РИС. 30.4 (q0 — заряд конденсатора при t = 0). 0 t
2. Слабое затухание (β < ω0) |
Рис. 30.4 |
|
Корни характеристического уравнения (30.9) — комплексные. Общее решение дифференциального уравнения (30.8)
β i ω2 β2 t β i ω2 β2 t i ω2 β2t i ω2 β2t
q t A1e 0 A2e 0 e βt A1e 0 A2e 0 .
Обозначим
ω
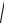ω02 β2
—циклическая частота свободных затухающих колебаний. Общее решение удобно представить в виде
q t A0e βt cos ωt φ |
, |
(30.10) |
где A0 и φ — постоянные интегрирования, значения которых определяются из начальных условий.
Период затухающих колебаний (условный период)
Амплитуда затухающих колебаний
A t A0e βt ;
247
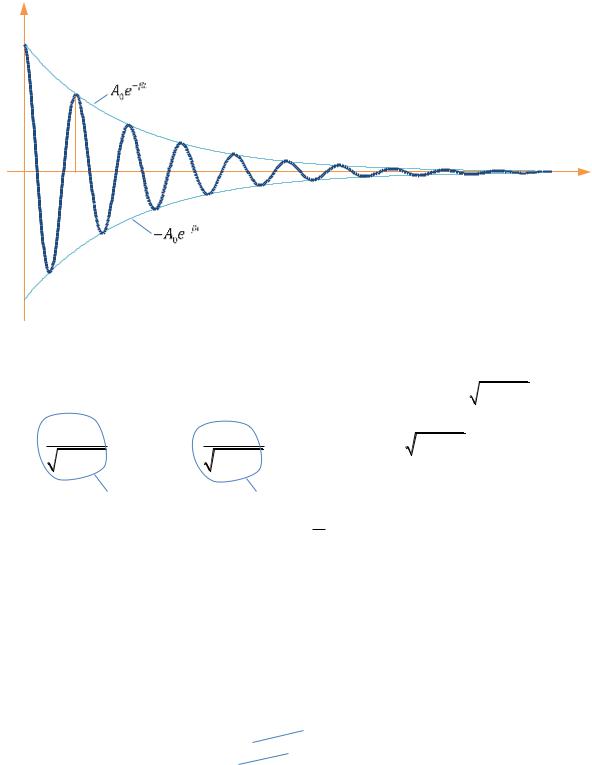
затухающие колебания можно рассматривать как гармонические колебания с переменной амплитудой:
q
График функции (30.10) при φ = 0 q
t Acos ωt φ .
показан на РИС. 30.5.
Рис. 30.5
Зависимость тока в цепи от времени
|
I t |
dq |
A e |
βt |
βcos ωt φ ωsin ωt φ |
A e |
βt |
|
β |
2 |
|
2 |
|
|
|
|
|
|
|
ω |
|
|
|
|
|
dt |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
cos ωt φ |
|
ω |
sin ωt |
|
A e |
βt |
β |
2 |
ω sin ωt φ θ ; |
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
β |
2 |
ω |
|
|
|
|
|
|
β |
2 |
ω |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin θ |
|
|
|
|
|
cos θ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tgθ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ток опережает заряд (напряжение на конденсаторе) по фазе на |
π |
θ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Введём ещё некоторые характеристики затухающих колебаний. |
|
|
|
|
|
|
Логарифмический декремент затухания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ ln |
A t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A t T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим логарифмический декремент через другие характеристики колебаний:
δ ln |
A e βt |
2πβ |
A e βte βT βT |
ω . |
|
0 |
|
|
|
0 |
|
|
Время релаксации — время, за которое амплитуда затухающих колебаний уменьшается в e раз:
248
A t |
|
A e |
|
|
|
|
|
|
|
|
|
βt |
|
|
|
|
|
e |
0 |
|
|
e |
βτ |
e βτ 1 |
, |
A t τ |
A e |
βt |
e |
βτ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
1 |
. |
|
|
|
|
|
|
β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число колебаний за время релаксации, т. е. число колебаний, за которое их ам-
плитуда уменьшается в e раз,
Ne Tτ βT1 δ1 .
Отсюда ясен физический смысл логарифмического декремента затухания. Добротность колебательного контура
Эта величина пропорциональна числу колебаний, шается в e раз.
Энергия затухающих колебаний
за которое их амплитуда умень-
В колебательной системе с затуханием происходит диссипация энергии. Так как электрическое сопротивление цепи отлично от нуля, энергия электромагнитного поля переходит во внутреннюю энергию проводников.
Энергия колебаний пропорциональна квадратам амплитуд всех колеблющихся ве-
Относительное уменьшение энергии за период |
|
|
W |
|
W t W t T |
|
1 e 2βT 1 e 2δ . |
|
|
|
|
W |
W t |
|
|
|
|
|
При малом затухании (δ << 1) |
W |
2δ |
. Тогда |
|
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
2π |
|
2πW |
. |
|
|
|
|
W |
W |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W |
|
|
|
|
Чем выше добротность колебательной системы, тем медленнее убывает энергия колебаний.
3.13.3. Вынужденные колебания
1 C |
2 L |
R |
Теперь включим в колебательный контур источник с перемен- |
ной ЭДС (РИС. 30.6), изменяющейся по гармоническому закону: |
|
|
|
|
|
|
|
|
|
E U0 cosΩt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
— вынуждающая ЭДС. |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
Обобщённый закон ома для участка 12: |
|
|
Рис. 30.6 |
φ1 φ2 E Es IR .(30.11) |
|
|
|
Подставив сюда (30.2) и (30.3), получим
с учётом I
Обозначим,
вид
|
q |
U0 cosΩt L |
dI |
IR ; |
|
C |
dt |
|
|
|
|
|
|
2 |
|
|
|
|
dq |
|
q |
|
|
|
|
|
|
|
|
L |
d q |
R |
|
U |
|
cosΩt , |
|
dt |
2 |
dt |
|
C |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
R dq |
|
|
q |
|
U |
|
|
|
|
|
d q |
|
|
|
cosΩt . |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
2 |
|
|
L dt |
|
|
LC |
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
R |
2β , а также |
U0 |
F0 |
LC |
ω0 |
, |
L |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
dq |
|
|
|
|
|
|
|
|
|
|
|
d q |
|
2β |
|
|
2 |
|
F cosΩt |
|
|
|
|
2 |
|
|
|
ω q |
|
|
dt |
|
|
|
|
dt |
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Уравнение (30.11) примет
(30.12)
— дифференциальное уравнение вынужденных гармонических колебаний. Это неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами.
Далее рассматриваем случай СЛАБОГО ЗАТУХАНИЯ.
Общее решение дифференциального уравнения (30.12):
q t A0e |
βt |
cos ωt φ q0 cos Ωt φ0 |
. |
|
общее решение ОДУ частное решение НДУ
Общее решение однородного дифференциального уравнения [(30.8) или (30.12) без правой части] быстро затухает, далее мы его учитывать не будем. Найдём коэффициенты q0 и φ0 в частном решении неоднородного уравнения [и убедимся в том, что это решение действительно имеет вид второго слагаемого в правой части выражения (30.13)].
Подставим в (30.12): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q t q0 cos Ωt φ0 |
, |
|
|
|
|
|
I t |
dq |
Ωq0 sin Ωt φ0 |
, |
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
d q |
|
|
|
2 |
|
|
; |
|
|
|
|
|
2 |
Ω q cos Ωt φ |
|
|
|
|
dt |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2βΩq sin |
Ωt φ |
2 |
|
|
|
F cosΩt |
Ω q cos Ωt φ |
ω q cos Ωt φ |
0 |
0 |
|
|
0 |
|
|
0 |
0 |
0 |
|
0 |
0 |
Преобразуем левую часть этого равенства:
